C++中的堆及常见题目汇总

目录

一、 数据结构之堆的基本知识

1. 完全二叉树
   1. 完全二叉树的概念
   2. 完全二叉树的重要性质
   3. 完全二叉树的存储　　
2. 堆的特性
   1. 最大堆
      1. 最大堆的特性
      2. 最大堆的实现逻辑（包括插入、删除等）　　
         1. 插入
         2. 删除　　　　
3. 基于堆的优先队列
4. C++中优先队列(priority_queue)详解

二、数据结构之堆-常见题目汇总

1. 最小堆
   1. 前k个高频元素　　
   2. 前k个高频单词
   3. 剑指offer 40: 最小的K个数
   4. 丑数
   5. 超级丑数
   6. 第k个数
2. 最大堆
   1. 数组的第k个最大元素　　
   2. 有序矩阵中第k小的元素
   3. 最后一块石头的重量
   4. 最小k个数
   5. 重构字符串
   6. 最接近原点的K个点
   7. 查找和最小的K对数字

 

 

一、 数据结构之堆的基本知识

1. 完全二叉树

　1.1完全 二叉树的概念

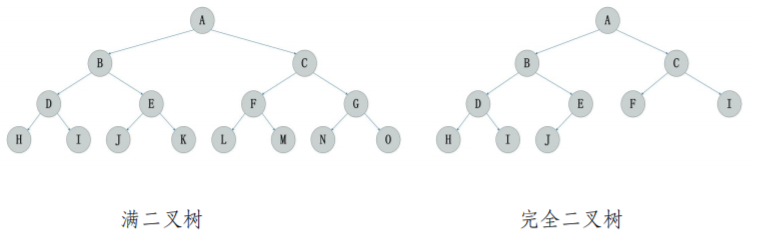
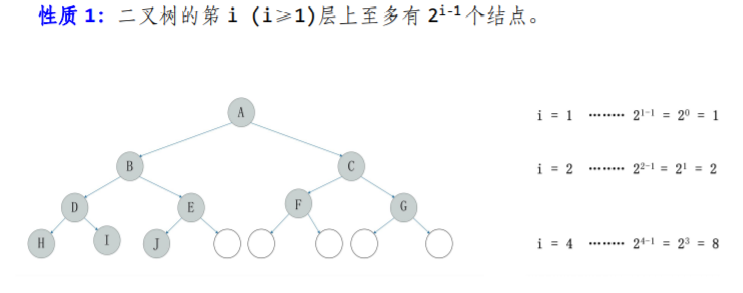
　如果一棵树深度为k，有n个结点的二叉树中各节点能与深度为k的顺序编号的满二叉树从1到n标号的节点相对应的二叉树成为完全二叉树，如下图所示

        

 

 

 　　1.2 二叉树的重要性质

　　

 

 

 　　

 

 

 　　

 

 

 　　

 

 

 　　1.3 二叉树的存储

• 线性存储

　　线性存储一般仅用于满二叉树和完全二叉树

• • 满二叉树的线性存储

　　

 

 

• • 一般二叉树的线性存储　　

　　

 2. 堆的特性

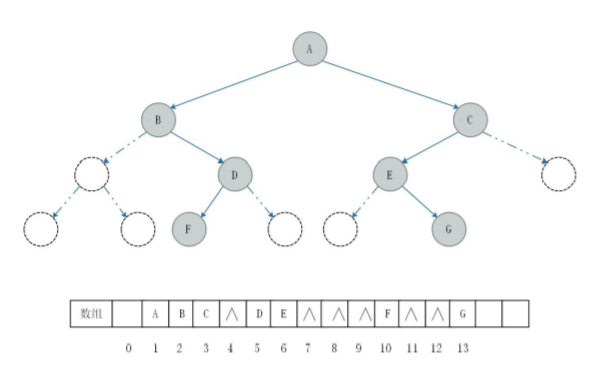
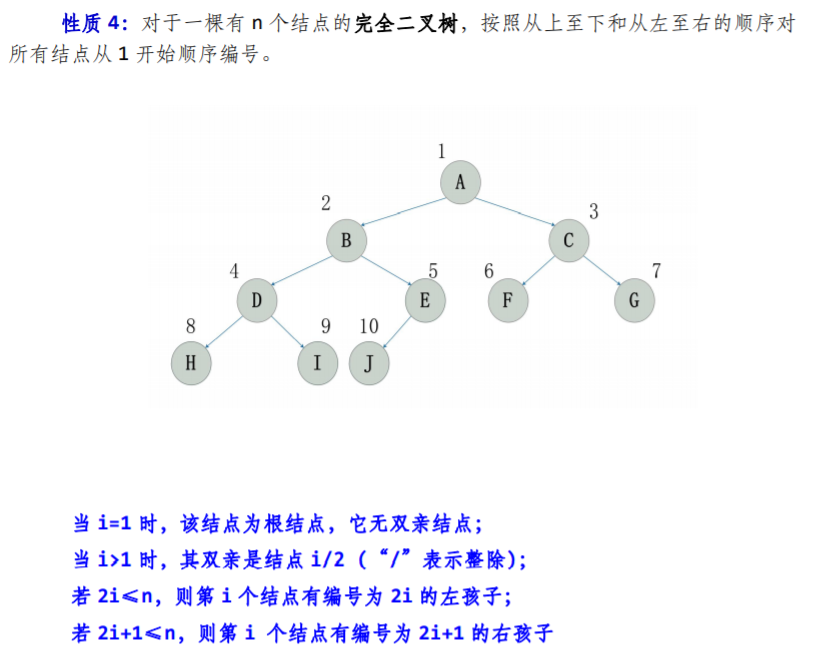
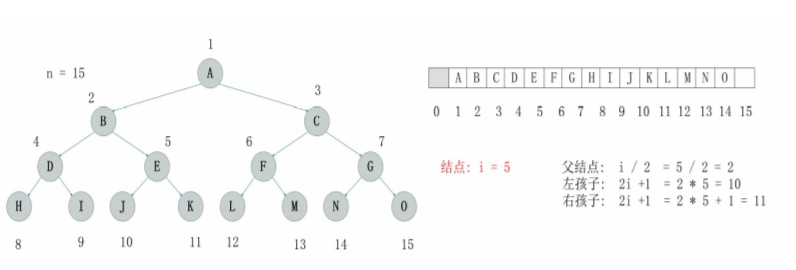
　　堆是数据结构中的一类，其可以看做是一颗完全二叉树的数组对象。因此，堆必须是完全二叉树，且用数组实现，任一节点是其子树所有节点的最大值或最小值。

　　

　　最小堆：完全二叉树，每个节点的元素值不大于其他节点的元素值。

　　2.1 最大堆

• 最大堆的概念　　

　　最大堆：完全二叉树，每个结点的元素值不小于其子节点的元素值

• 最大堆的实现逻辑（包括插入、删除等）　　
  • 插入

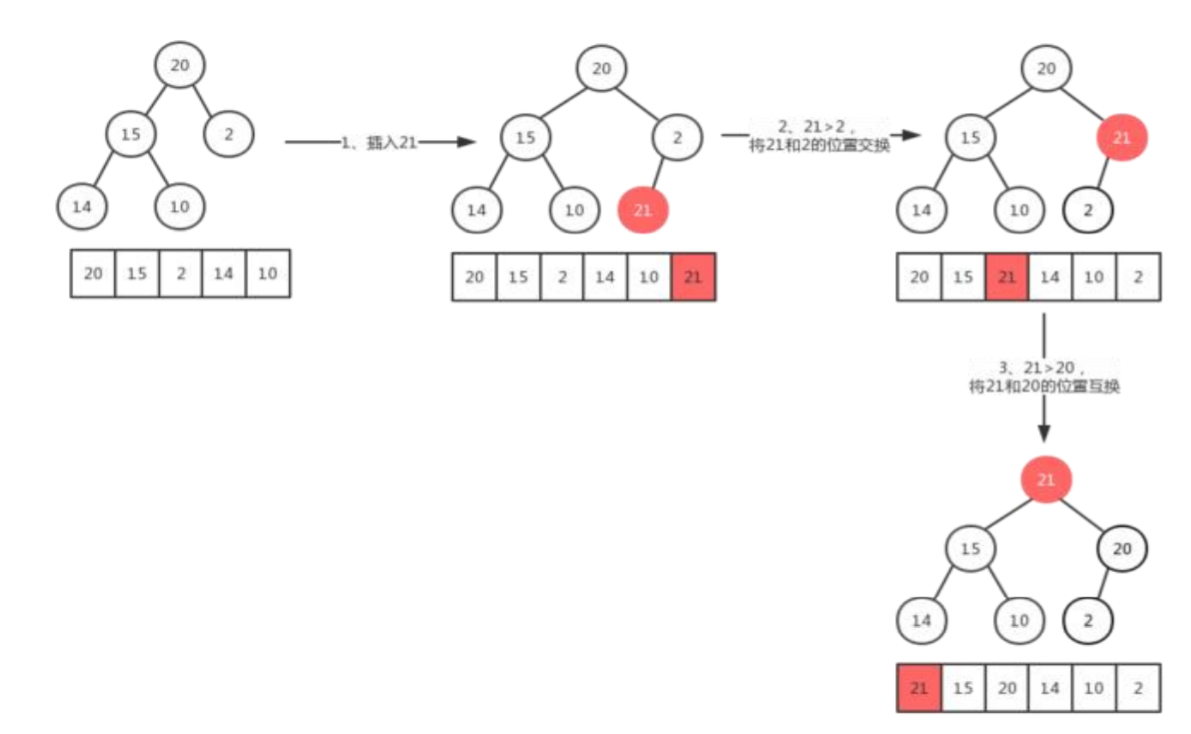
　　　　　　最大堆的插入操作可以简单看成是“结点上浮”。当我们向最大堆中插入一个结点，我们必须满足完全二叉树的标准，那么被插入节点的位置是固定的。而且要满足父节点关键字值不小于子节点关键字值，我们需要移动父节点和子节点的相互位置关系。

　　　　

 

• •  删除

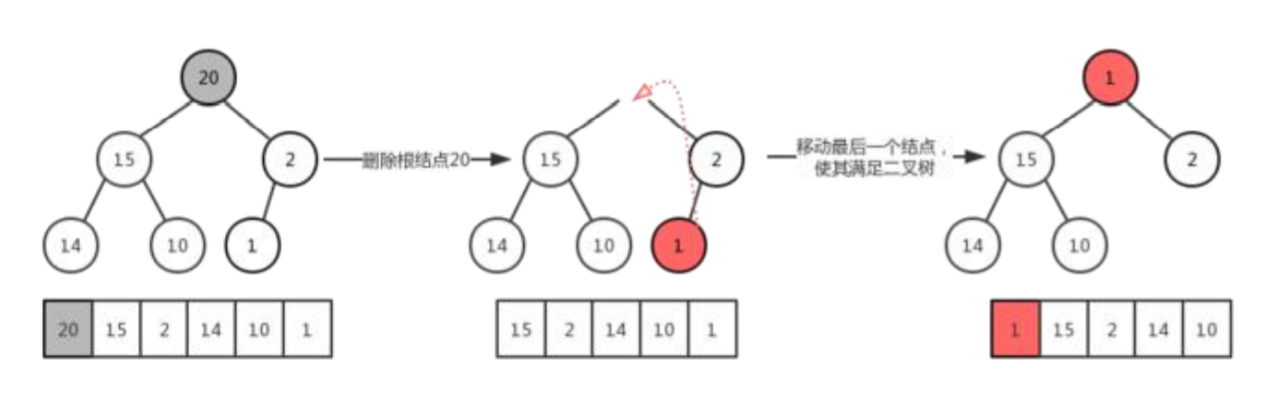
　　　　最大堆的删除操作，总是从堆的根节点删除元素。同样根元素被删除之后为了能够保证树还是一颗完全二叉树，我们需要移动完全二叉树的最后一个节点，使其继续符合完全二叉树的定义，从这里可以看做是最大堆最后一个节点的下沉。

　

 

 　　此时是满足完全二叉树的要求，但是仍然不满足根节点是最大值的要求，继续调整如下：

　　

 

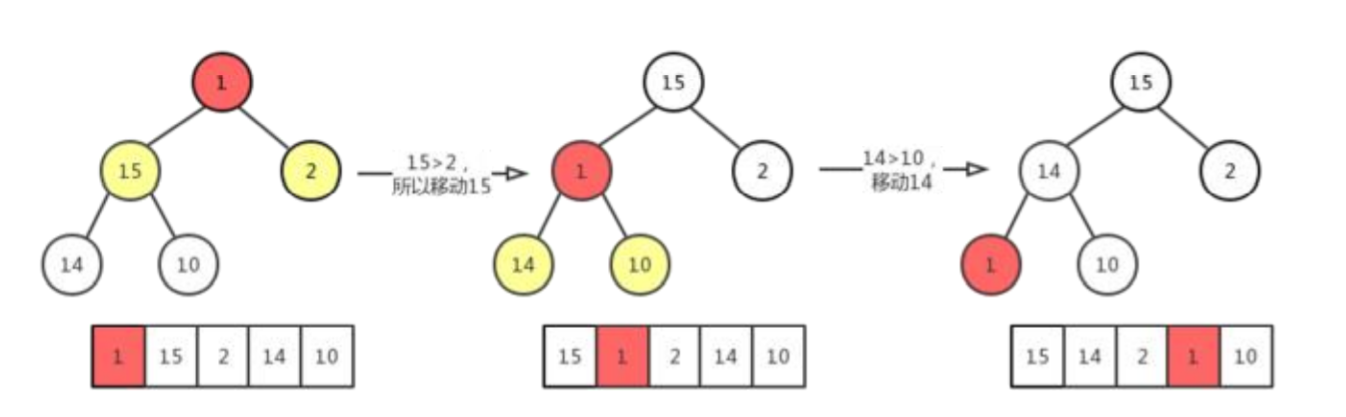
 　　在这里已经确定的最大堆中做删除操作，被删除的元素是固定的，需要被移动的节点也是固定的，这里我说的被移动元素是指最初的移动，即最大堆的最后一个元素，移动方式为从最大的节点开始比较。

 3. 基于堆的优先队列

　　我们知道，普通的队列的特点是先进先出。先入队列的元素自然会先出队列。

　　优先队列将不再遵循先入先出的原则，而是分为两种情况

　　最大优先队列，无论入队顺序，都是当前最大的元素优先出队列--基于最大堆

　　最小优先队列，无论入队顺序，都是当前最小的元素优先出队列--基于最小堆

　　比如有一个最大优先队列，其最大的元素是8，那么虽然元素8不是队首元素，但是出队时仍然让元素8优先出队

　　

 

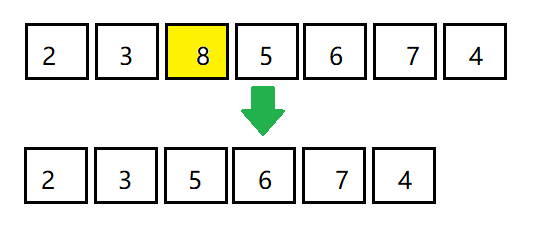
 　　要满足上述需求，利用线性数据结构并非不能实现，但是时间复杂度较高，最坏时间复杂度是O(n)并不是最理想的方式，因此我们使用二叉堆来实现优先队列。

　　二叉堆的特性

　　最大堆：堆顶元素是整个堆中最大元素

　　最小堆：堆顶元素是整个堆中最小元素

　　入队和出队操作刚刚已经介绍过。

4. C++中优先队列priority_queue介绍

　　优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出(first in, largest out)的行为特征

　　priority_queue<Type, Container, Functional>

• type就是数据类型
• Container就是容器类型(Container必须是数组实现的容器，如vector,deque等，但不能用list，STL中默认的是vector)
• Functional就是比较的方式　　

　　当需要用自定义的数据类型时才需要传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大堆顶

　　一般是

//升序队列，小堆顶
priority_queue<int, vector<int>,greater<int> > q;
//降序队列，大堆顶
priority_queue<int, vector<int>, less<int> > q;

• 基本类型优先队列的例子

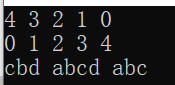
#include<iostream>
#include <queue>
using namespace std;
int main()
{
    //对于基础类型 默认是大顶堆
    priority_queue<int> a;
    //等同于 priority_queue<int, vector<int>, less<int> > a;

    //      这里一定要有空格，不然成了右移运算符↓↓
    priority_queue<int, vector<int>, greater<int> > c;  //这样就是小顶堆
    priority_queue<string> b;

    for (int i = 0; i < 5; i++)
    {
        a.push(i);
        c.push(i);
    }
    while (!a.empty())
    {
        cout << a.top() << ' ';
        a.pop();
    }
    cout << endl;

    while (!c.empty())
    {
        cout << c.top() << ' ';
        c.pop();
    }
    cout << endl;

    b.push("abc");
    b.push("abcd");
    b.push("cbd");
    while (!b.empty())
    {
        cout << b.top() << ' ';
        b.pop();
    }
    cout << endl;
    return 0;
}

　　运行结果如下：

　　 

 

•  用pair做优先队列元素的例子

　　规则：pair的比较，先比较第一个元素，若第一个相等比较第二个

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main()
{
    priority_queue<pair<int, int> > a;
    pair<int, int> b(1, 2);
    pair<int, int> c(1, 3);
    pair<int, int> d(2, 5);
    a.push(d);
    a.push(c);
    a.push(b);
    while (!a.empty())
    {
        cout << a.top().first << ' ' << a.top().second << '\n';
        a.pop();
    }
}

　　运行结果

　　

 

 二、数据结构之堆-常见题目汇总

1. 最小堆

　　1.1 前K个高频元素

• 题目描述

　　

 

•  问题分析

　　首先建立一个哈希表，统计非空数组中每个元素出现的次数

　　建立一个最小堆，最小堆尺寸大于k时，则将堆顶元素出栈

　　由于最小堆是从小到大，因此要一次输出出现频率前k高的元素，倒序打印

• 代码分析

　

class Solution {
public:
    class mycomparison{
    public:
        bool operator()(const pair<int,int>& fsh,const pair<int,int> &ssh)
        {
            return fsh.second>ssh.second;
        }
    };
    vector<int> topKFrequent(vector<int>& nums, int k) {
        vector<int> B(k);
        if(nums.empty())
            return B;
        //首先建立一个哈希表，统计非空数组中每个元素出现的次数
        unordered_map<int,int> map;
        for(int i=0;i<nums.size();++i)
        {
            map[nums[i]]++;
        }
        //建立一个最小堆，最小堆尺寸大于k是则将堆顶元素出栈
        priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparison> pri_que;
        for(unordered_map<int,int>::iterator it=map.begin();it!=map.end();++it)
        {
            pri_que.push(*it);
            if(pri_que.size()>k)
                pri_que.pop();
        }
        //由于最小堆是从小到大，因此要一次输出出现频率前k高的元素，倒序打印
        for(int i=k-1;i>=0;--i)
        {
            B[i]=pri_que.top().first;
            pri_que.pop();
        }
        return B;
    }
};

 

　　1.2 前k个高频单词

• 题目描述

　　

 

• 问题分析

　　为了找到前k个高频单词，采用算法如下：

　　　　首先统计字符串数组中每个字符串出现的次数。

　　　　建立最小堆，维护一个大小为k的最小堆，优先级小的元素在堆顶，每当某个新来的元素的优先级高于小顶堆的优先级时，将这个元素进堆，然后pop掉优先级最小的元素，堆的大小还是k。

　　　　优先级的判定需要重载()（注意一定要重载这个括号运算符而不是其他，因为末尾的greater<T>和less<T>里面也是重载的()），这里我们需要的是greater的功能，也就是说，需要优先级小的元素在堆顶。

• 代码参考

　　

class Solution {
public:
    struct compare{
    public:
        bool operator() (const pair<int,string> &a,const pair<int,string> &b)
        {
            return (a.first>b.first||a.first==b.first&&a.second<b.second);
        }
    };
    vector<string> topKFrequent(vector<string>& words, int k) {
        vector<string> B(k);
        if(words.empty()||k<=0)
            return B;
        unordered_map<string,int> map;
        compare ord;
        //首先统计每个单词出现的次数
        for(int i=0;i<words.size();++i)
        {
            map[words[i]]++;
        }
        priority_queue<pair<int,string>,vector<pair<int,string>>,compare > q;
        for(auto it:map)
        {
            pair<int,string> temp{it.second,it.first};
            q.push(temp);
            if(q.size()>k)
                q.pop();
        }
        for(int i=k-1;i>=0;--i)
        {
            B[i]=q.top().second;
            q.pop();
        }
        return B;
    }
};

 

 

　　1.2 剑指offer 40: 最小的k个数

• 题目描述

　　

 

•  问题分析

　　要找到最小的K个数，可以使用最小堆来实现，依次弹出K个堆顶元素即可找到最小的k个元素

• 代码参考

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        vector<int> B(k);
        if(arr.empty())
            return B;
        priority_queue<int,vector<int>,greater<int> > pri_que;
        for(int i=0;i<arr.size();++i)
        {
            pri_que.push(arr[i]);
        }
        for(int i=0;i<k;++i)
        {
            B[i]=pri_que.top();
            pri_que.pop();
        }
        return B;
    }
};

 

　1.3 丑数

• 题目描述

　　

 

 

 

• Solution 1：使用常规方法
  • 问题分析1　　

　　　　丑数应该是另一个丑数乘以2,3,5的结果。对于乘以2而言，肯定存在一个丑数T2，排在他之前的每个丑数乘以2得到的结果都会小于已有最大的丑数，在他之后的丑数乘以2得到的结果都会太大，我们只需要记下这个丑数的位置，每次生成新的丑数的时候去更新这个T2即可

• • 代码参考1

　　

class Solution {
public:
    //最小的丑数是2,3,5，后面的丑数一定是丑数乘以2,3,5，取最小的得到的
    int Min(int a,int b,int c)
    {
        int min=a<b?a:b;
        min=min<c?min:c;
        return min;
    }
    int nthUglyNumber(int n) {
        if(n<=0)
            return 0;
        int *uglynumbers=new int [n+1];
        uglynumbers[0]=1;
        int *M2=uglynumbers;
        int *M3=uglynumbers;
        int *M5=uglynumbers;
        int nextuglynumbers=1;
        while(nextuglynumbers<n)
        {
            int min=Min(*M2*2,*M3*3,*M5*5);
            uglynumbers[nextuglynumbers]=min;
            while(*M2*2<=min)
                ++M2;
            while(*M3*3<=min)
                ++M3;
            while(*M5*5<=min)
                ++M5;
            ++nextuglynumbers;
        }
        int ugly=uglynumbers[nextuglynumbers-1];
        delete[]uglynumbers;
        return ugly;
    }
};

• Solution2 利用最小堆实现
  • 问题分析2

　　　　　　由于丑数都是另一个丑数乘以2,3,5得到的，可以利用优先队列实现自动排序功能。

　　　　　　每次去除队头元素，存入队头元素*2，队头元素*3，队头元素*5

　　　　　　但是需要去重，因为想12这个元素，可以由3*4得到，也可以由2*6得到

• • 代码参考2

class Solution {
public:
    int nthUglyNumber(int n) {
        if(n<=0)
            return 0;
        priority_queue<double,vector<double>,greater<double> >q;
        double answer=1;
        for(int i=1;i<n;++i)
        {
            q.push(answer*2);
            q.push(answer*3);
            q.push(answer*5);
            answer=q.top();
            q.pop();
            while(!q.empty()&&answer==q.top())
                q.pop();
        }
        return answer;
    }
};

 

　　1.5 超级丑数

•  题目描述

　　

 

 

•  Solution 1--利用数组特性来做
  • 问题分析1

　　　　分析超级丑数和丑数的区别是：超级丑数的因子为质数列表primes中的元素，数组长度是未定的

　　　　在循环的过程中，可以先设置一个变量mini保存指针在uglynumbers中的位置对应的值x自身prime值的最小值，接着再循环一次将所有的指针位置进行更新

• • 代码参考1

class Solution {
public:
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n<=0)
            return 0;
        int k=primes.size();
        vector<int> uglynumbers(n);
        vector<int> kv(k,0);//用来记录这k个数的指针位置，初始化为0
        int nextuglynumber=1;
        uglynumbers[0]=1;
        while(nextuglynumber<n)
        {
            int mini=INT_MAX;
            for(int j=0;j<k;++j)
            {
                mini=min(mini,uglynumbers[kv[j]]*primes[j]);
            }
            uglynumbers[nextuglynumber]=mini;
            for(int j=0;j<k;++j)
            {
                if(mini==uglynumbers[kv[j]]*primes[j])
                    kv[j]++;
            }
            ++nextuglynumber;
        }
        return uglynumbers[nextuglynumber-1];
    }
};

• solution 2--利用堆
  • 问题分析2　　

　　　　　　由于丑数都是另一个丑数乘以primes[i]得到的，可以利用优先队列实现自动排序功能。

　　　　　　每次去除队头元素，存入队头元素*primes[i];

　　　　　　但是需要去重

• • 代码参考2

class Solution {
public:
    int nthSuperUglyNumber(int n, vector<int>& primes) {
        if(n<=0)
            return 0;
        priority_queue<long long,vector<long long>,greater<long long> >pq;
        long long answer=1;
        int k=primes.size();
        for(int i=1;i<n;++i)
        {
            for(int i=0;i<k;++i)
            {
                pq.push(answer*primes[i]);
                
            }
            answer=pq.top();
            pq.pop();
            while(!pq.empty()&&answer==pq.top())
                pq.pop();
        }
        return answer;
    }
};

 

　　1.6 第k个数

• 题目描述

　　

 

 

•  问题分析

　　这道题类似于丑数的算法，我们将要找到的数称为丑数要得到有序的丑数数组，我们可以用前面的丑数乘以3,5,7，取最小值放入丑数数组即可。

　　

class Solution {
public:
    int Min(int a,int b,int c)
    {
        int min=a<b?a:b;
        min=min<c?min:c;
        return min;
    }
    int getKthMagicNumber(int k) {
        if(k<=0)
            return 0;
        int *uglynumbers=new int[k+1];
        uglynumbers[0]=1;
        int *M3=uglynumbers;
        int *M5=uglynumbers;
        int *M7=uglynumbers;
        int nextuglynumbers=1;
        while(nextuglynumbers<k)
        {
            int mini=Min(*M3*3,*M5*5,*M7*7);
            uglynumbers[nextuglynumbers]=mini;
            while(*M3*3<=mini)
                ++M3;
            while(*M5*5<=mini)
                ++M5;
            while(*M7*7<=mini)
                ++M7;
            ++nextuglynumbers;
        }
        return uglynumbers[nextuglynumbers-1];
    }
};

 

• 问题分析2

　　也可以用最小堆来实现，算法如下：

　　　　由于丑数都是另一个丑数乘以3,5,7得到的，可以利用优先队列实现自动排序功能。

　　　　每次去除队头元素，存入队头元素*3，队头元素*5，队头元素*7

　　　　但是需要去重

• 代码参考2

　　

class Solution {
public:
    int getKthMagicNumber(int k) {
        if(k<=0)
            return 0;
        priority_queue<double,vector<double>,greater<double> > pq;
        double answer=1;
        for(int i=1;i<k;++i)
        {
            pq.push(answer*3);
            pq.push(answer*5);
            pq.push(answer*7);
            answer=pq.top();
            pq.pop();
            //去重
            while(!pq.empty()&&answer==pq.top())
                pq.pop();
        }
        return answer;
    }
};

 

　　

　　

2. 最大堆

 　　2.1 数组中的第k个最大元素

• 题目描述

　　

 

• solution 1
  • 问题分析(使用STL模板)

　　　　要实现找到未排序数组中第k个最大的元素，我们可以使用对排序

　　　　　　将数组中的元素建立一个最大堆，堆顶元素是最大的

　　　　　　要找到第k个最大元素，只需要删除k-1次堆顶元素，删除后堆顶元素即为第k个最大值

• • 代码参考

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        if(nums.empty())
            return 0;
        //建立一个最大堆，对于第k大元素，删除k-1次后，堆顶元素就是数组排序后第k个最大的元素
        priority_queue<int> pri_que;
        for(int i=0;i<nums.size();++i)
        {
            pri_que.push(nums[i]);
        }
        //删除k-1次堆顶元素
        for(int i=0;i<k-1;++i)
            pri_que.pop();
        return pri_que.top();
    }
};

• solution2 (自己实现最大堆，包括最大堆的建堆，调整以及删除)
  • 问题分析

 

• •  代码参考　　

class Solution {
public:
    //自己实现，要实现三个部分
    //首先是堆化
    //完全二叉树中，对于节点i，父节点为i/2,左子节点为i*2+1,右子节点为i*2+2
    void maxHeapify(vector<int> &a,int i,int heapSize)
    {
        //左子节点
        int l=i*2+1;
        //右子节点
        int r=i*2+2;
        int largest=i;
        if(l<heapSize&&a[l]>a[largest])
            largest=l;
        if(r<heapSize&&a[r]>a[largest])
            largest=r;
        if(largest!=i)
        {
            swap(a[i],a[largest]);
            maxHeapify(a,largest,heapSize);
        }
    }
    //建立堆
    void buildMaxHeap(vector<int> &a,int heapSize)
    {
        //从第一个非叶子节点为根节点的子树开始，将其调整为最大堆
        for(int i=heapSize/2;i>=0;--i)
        {
            maxHeapify(a,i,heapSize);
        }
    }    
    int findKthLargest(vector<int>& nums, int k) {
        int heapSize=nums.size();
        buildMaxHeap(nums,heapSize);
        for(int i=nums.size()-1;i>=nums.size()-k+1;--i)
        {
            swap(nums[0],nums[i]);
            --heapSize;
            maxHeapify(nums,0,heapSize);
        }
        return nums[0];

    }
};

 

　

　2.2 有序矩阵中第k小的元素

• 题目描述

　　

•  solution1--最大堆
  • 问题分析1

　　　　要找到第k小的元素，一种最常规的做法就是使用优先队列

　　　　　　找第k小的元素，保留k个最小的元素，其中最大的那个就是答案，所以可以使用最大优先队列

　　　　　　遍历矩阵中的元素，将元素添加到队列中，如果队列中元素数目>k，则将堆点最大的元素弹出

　　　　　　遍历结束后弹出堆顶元素，就是最小的k个元素中最大的，即第k小的元素

• • 代码参考1　

 1 class Solution {
 2 public:
 3     int kthSmallest(vector<vector<int>>& matrix, int k) {
 4         if(matrix.empty())
 5             return 0;
 6         priority_queue<int> pri_que;
 7         for(int i=0;i<matrix.size();++i)
 8         {
 9             for(int j=0;j<matrix[0].size();++j)
10             {
11                 pri_que.push(matrix[i][j]);
12                 if(pri_que.size()>k)
13                     pri_que.pop();
14             }
15         }
16         return pri_que.top();
17     }
18 };

• solution2 --二分查找
  • 问题分析2

　　　　　　方法1的方式没有用上矩阵的有序性，因此我们可以思考使用二分查找的方法

　　　　　　对于有序矩阵中，左上角元素是最小元素，右下角元素是最大元素

　　　　　　因此我们可以使用二分查找的方法,left=左上角元素，right=右下角元素

　　　　　　mid=left+(right-left)/2;统计大于mid的个数

　　　　　　　　如果小于mid的元素个数小于k，则比mid大的数可能是第k小元素

　　　　　　　　如果小于mid的元素个数大于k，则比mid小的数可能是第k小元素

　　　　　　在这里我们使用upper_bound来统计小于mid的元素个数

　　　　　　upper_bound()

　　　　　　upper_bound( begin,end,num)：从数组的begin位置到end-1位置二分查找第一个大于num的数字，找到返回该数字的地址，不存在则返回end。通过返回的地址减去起始地址begin,得到找到数字在数组中的下标。

• • 代码参考2

class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        //有序矩阵中，左上角元素是最小的，右下角元素是最大的
        /*
        left=matrix[0][0],right=matrix[n][n],mid=left+(left-right)/2
        统计大于mid的个数，
            如果小于mid的元素个数小于k，则比mid大的数可能是第k小元素
　　　　　　　如果小于mid的元素个数大于k，则比mid小的数可能是第k小元素
        */
        if(matrix.empty())
            return 0;
        int n=matrix.size()-1;
        int left=matrix[0][0];
        int right=matrix[n][n];
        int mid;
        
        while(left<right)
        {
            int ans=0;
            mid=left+(right-left)/2;
            for(int i=0;i<matrix.size();++i)
            {
                ans+=upper_bound(matrix[i].begin(),matrix[i].end(),mid)-matrix[i].begin();
            }
            if(ans<k)
                left=mid+1;
            else
                right=mid;
        }
        return left;
    }
};

 

　　2.3 最后一块石头的重量

• 题目描述

　　

 

•  问题分析

　　有题意，最大堆即可解决问题，弹出最大的两个数据，若两个数据之差为0，则不用再次压入最大堆，否则将二者之差压入最大堆

• 代码参考

　　

class Solution {
public:
    int lastStoneWeight(vector<int>& stones) {
        if(stones.empty())
            return 0;
        priority_queue<int> pri_que(stones.begin(),stones.end());
        while(pri_que.size()>1)
        {
            int biggest=pri_que.top();
            pri_que.pop();
            int second=pri_que.top();
            pri_que.pop();
            int substraction=biggest-second;
            if(substraction>0)
                pri_que.push(substraction);
        }
        if(pri_que.size()>0)
            return pri_que.top();
        else
            return 0;
    }
};

 

　　2.4 根据字符出现频率排序

• 题目描述

　　

 

•  问题分析

　　要给字符串中的字符按照出现频率升降排序，可以采用以下算法

　　　　首先统计字符串中所有字符出现的次数，存储在哈希表中

　　　　根据字符串中所有字符出现的次数构造最大堆

　　　　依次输出

• 代码参考

class Solution {
public:
    string frequencySort(string s) {
        if(s.empty())
            return "";
        unordered_map<char,int> map;
        //首先统计每个字符出现的次数
        for(int i=0;i<s.size();++i)
        {
            map[s[i]]++;
        }
        //根据每个字符出现的次数，建立一个最大堆
        priority_queue<pair<int,char>> pri_que;
        for(auto &m:map)
        {
           pri_que.push({m.second,m.first});
        }
        string res;
        while(!pri_que.empty())
        {
            auto t=pri_que.top();
            pri_que.pop();
            res.append(t.first,t.second);
        }
        return res;
    }
};

 

　　2.4 最小k个数

• 题目描述

　　

 

 

•  问题分析

　　要找到数组中最小的k个数，可以使用大堆顶来实现，将数组中的每个元素都压栈入大堆顶，如果最大堆的元素个数大于k，则将最大堆的堆顶元素删除

• 代码参考

　　

class Solution {
public:
    vector<int> smallestK(vector<int>& arr, int k) {
        vector<int> B;
        if(arr.empty()||k<=0)
            return B;
        priority_queue<int,vector<int>,less<int> >q;
        for(int i=0;i<arr.size();++i)
        {
            q.push(arr[i]);
            if(q.size()>k)
                q.pop();
        }
        while(!q.empty())
        {
            B.push_back(q.top());
            q.pop();
        }
            
        return B;
    }
};

 

　　2.5 重构字符串

• 问题描述

　　

 

•  问题分析

　　要判断是否可以重构字符串，可以采用算法如下

　　　　首先构建哈希表统计字符串中每个字符出现的次数，如果字符串中某个字符出现的次数超过字符串长度的一半，则不能重构字符串

　　　　然后构建一个最大堆，将哈希表中的键值对根据出现次数构建成一个最大堆

　　　　然后按照字母数量降序顺序，当队列不为空时，一次按照堆顶元素，隔着往原始字符串中插入当前字符，下标从0开始，每次插入下标+2，当超过数组大小时，变为1

• 代码参考

class Solution {
public:
    string reorganizeString(string S) {
        //哈希表+最大堆
        /*
        构造一个哈希表，其首先统计字符串中每个字符出现的次数
        将哈希表字符及字符出现的次数压入大顶堆中
        依次插入一个长度与S等长的字符串中
        */
        if(S.empty())
            return "";
        //首先统计字符串中每个字符出现的次数，并将其存储在哈希表中
        unordered_map<char,int> map;
        for(int i=0;i<S.size();++i)
        {
            map[S[i]]++;
            if(map[S[i]]>(S.size()+1)/2)
                return "";
        }
            

        //构造一个大顶堆存储哈希表
        priority_queue<pair<int,char>,vector<pair<int,char>>> pq;
        for(auto item:map)
        {
            pq.push({item.second,item.first});
        }
        int i=0;
        string res=S;
        while(!pq.empty())
        {
            char ch=pq.top().second;
            int cnt=pq.top().first;
            pq.pop();
            while(cnt--)
            {
                i=i>=S.size()?1:i;
                res[i]=ch;
                i=i+2;
            }
        }
        return res;
    }
};

 

　　2.6 最接近原点的K个点

• 题目描述

　　

•  问题分析

　　要实现找到最接近原点的K个点，我们可以构造一个大小为K的最大堆，当最大堆的尺寸大于K时，将堆顶元素弹出，因此最后最大堆中剩下的就是距离原点最小的K个点

　　构建的最大堆每次输入为一个长度为2的vector数组，此时不是基本类型，因此需要重载运算符()

• 代码参考

class Solution {
public:
    //最大堆，因此需要重载()
    class compare{
    public:
        bool operator()(const vector<int>&a,const vector<int>&b)
        {
            return pow((pow(a[0],2)+pow(a[1],2)),0.5)<pow((pow(b[0],2)+pow(b[1],2)),0.5);
        }
    };
    vector<vector<int>> kClosest(vector<vector<int>>& points, int K) {
        vector<vector<int>> B;
        if(points.empty())
            return B;
        //构建最大堆
        priority_queue<vector<int>,vector<vector<int>>,compare> pq;
        for(int i=0;i<points.size();++i)
        {
            int distance=pow(pow(points[i][0],2)+pow(points[i][1],2),0.5);
            vector<int> temp={points[i][0],points[i][1]};
            pq.push(temp);
            if(pq.size()>K)
                pq.pop();
        }
        for(int i=0;i<K;++i)
        {
            B.push_back(pq.top());
            pq.pop();
        }
        return B;
    }
};

 

 　　2.7 查找和最小的k对数字

• 题目描述

　　

 

•  问题分析

　　要查找和最小的K对数字，我们可以将nums1的第i个元素和nums2的第j个元素相加，并将数据对存储在长度为K的最大堆上

• 代码参考

　　

class Solution {
public:
    class compare{
    public:
        bool operator()(const pair<int,int> &a,pair<int,int> &b)
        {
            return (a.first+a.second)<(b.first+b.second);
        }
    };
    vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        vector<vector<int>> B;
        if(nums1.empty()||nums2.empty())
            return B;
        
        priority_queue<pair<int,int>,vector<pair<int,int>>,compare> pq;
        for(int i=0;i<nums1.size();++i)
        {
            for(int j=0;j<nums2.size();++j)
            {
                pq.push({nums1[i],nums2[j]});
                if(pq.size()>k)
                    pq.pop();
            }
        }
        while(!pq.empty())
        {
            pair<int,int> top=pq.top();
            pq.pop();
            B.push_back({top.first,top.second});
        }
        return B;
    }
};