学习笔记 #4：树状数组和 LIS
学习笔记#4 ：树状数组和 LIS
前言：
树状数组是和线段树类似的数据结构，更确切的说，树状数组能解决的问题，线段树都能解决，而线段树还能解决一些树状数组所不能解决的问题。因此线段树的应用范围比树状数组更广泛。但是，树状数组的常数更小，在同样的 \(\text{O}(n\log n)\) 复杂度下，树状数组普遍运行得更快。虽然线段树中有 zkw 线段树这样的小常数线段树，但树状数组仍然是常数之王，并且它的码量也极其之小，因此还是有学习的必要。
原理 & 实现：
有图为证：
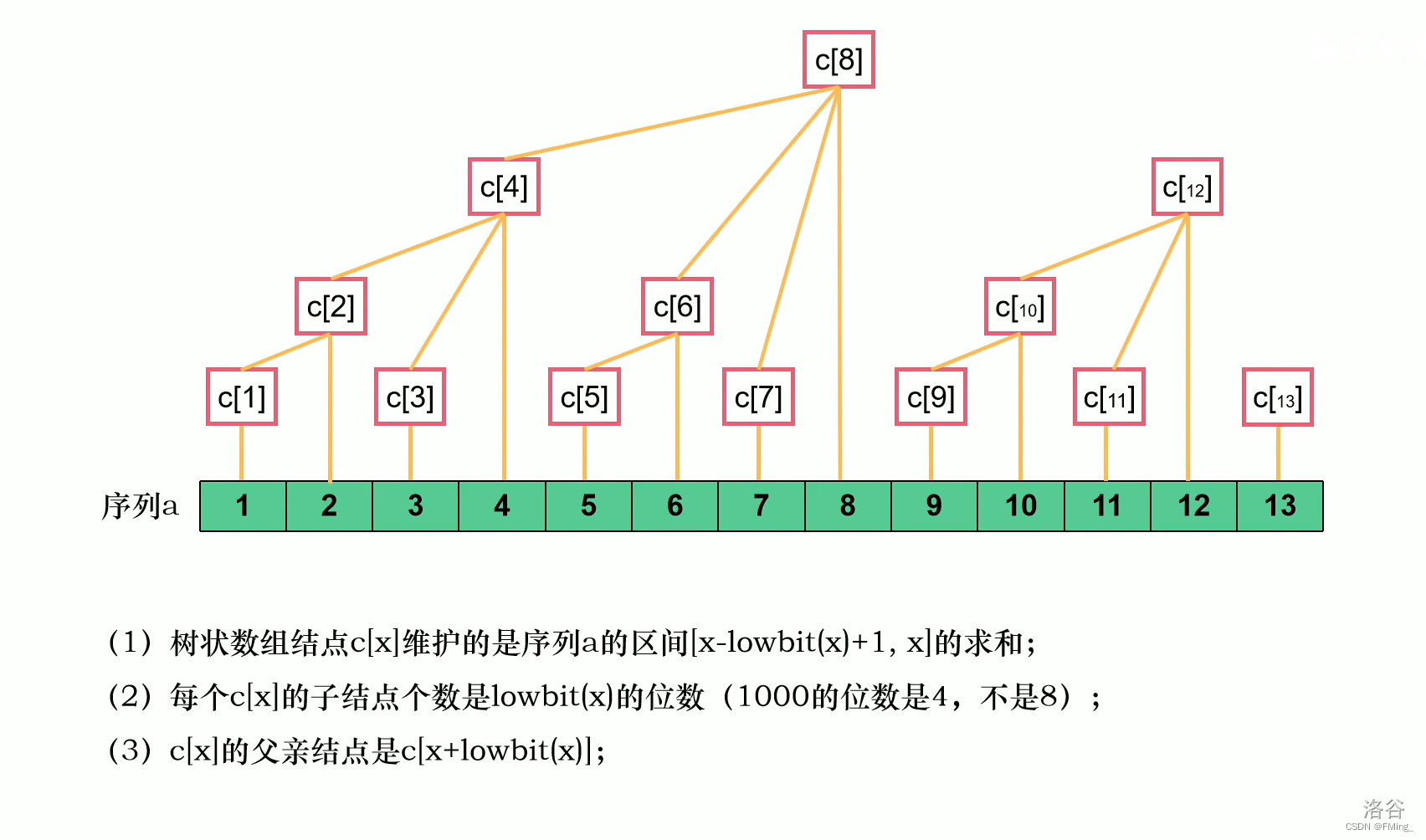
首先介绍 \(\text{lowbit}(x)\) 是什么：
\(\text{lowbit}(x)\)，顾名思义，就是二进制数 \(x\) 最低位的 \(1\) 所代表的十进制数，求法是 \(\text{lowbit}(x)=x\&-x\)，具体原理手玩一下就知道。
代码：
int lowbit(int x) {return x & -x;}
而上图中树状数组的结构，从十进制数看起来没什么规律，但如果转为二进制呢？
\(c[00001]=a[00001]\)
\(c[00010] = a[00001] + a[00010]\)
\(c[00011] = a[00011]\)
\(c[00100] = a[00001] + a[00010] + a[00011] + a[00100]\)
\(\dots\)
有什么规律？
从单个的 \(a\) 或 \(c\) 来看找不到规律，放眼全局，则可以看出：
- 从 \(1\) 加到 \(i\) 就是 \(i\) 一直 -= \(\text{lowbit}(i)\) 直到 \(i = 0\)。
- 每一个 \(a[i]\) 被 \(i\) 一直 += \(\text{lowbit}(i)\) 直到 \(i = n\) 的 \(c[i]\) 所管辖。
因此，树状数组的单点修改和区间查询就可以写出：
单点修改：
void modify(int i, int c) {for(; i <= n; i += lowbit(i)) C[i] += c;}
区间查询：
int query(int i) {int res = 0; for(; i; i -= lowbit(i)) res += C[i]; return res;}
int Query(int l, int r) {return Query(r) - Query(l - 1);}
树状数组与 LIS
LIS，即最长不下降子序列。
譬如这样一个序列：
1 2 4 1 3 4
显然，它的最长不下降子序列就是 1 2 3 4 ，长度为 \(4\)。
我们设 \(f[i]\) 为以 \(i\) 结尾的最长不下降子序列的长度，则有：
\(f[i] = \max(f[j] + 1) (j < i \&\& a[j] \le a[i])\)
很明显，复杂度 \(\text{O}(n^2)\)，对于很大的数据是过不了的。
那么怎么将复杂度降到 \(\text{O}(n \log n)\) 呢？
就要请出我们今天的主角：树状数组了。
首先，建立一棵值域树状数组：（如果 \(a[i]\) 过大就需要离散化）
这棵树状数组所维护的是以 \(a[i]\) 结尾的最长不下降子序列的长度，所以添加的时候 \(C[i] = \max(C[i], c)\)。而我们扫到哪加到哪，就保证了无后效性。
然后区间查询比 \(a[i]\) 小的，即以 \([1, a[i]]\) 结尾的最长不下降子序列的长度，加 \(1\) 即可。
\(Q.E.D.\)
