学习笔记 #1：树链剖分
说在前面
引言
树链剖分，是树上操作的常用算法，多用于求LCA、树上RSQ、树上RMQ等问题，与树上差分有共通之处。
前置知识
线段树
DFS序
图的存储与遍历
正文
有重链剖分和长链剖分两种方式，主流的方法是重链剖分，两者没太大区别，一个按siz，一个按dep而已。
我们要进行两次dfs：
第一次，处理 siz (子树大小)、fa (父亲)、son (重儿子，即作为根的子树大小最大的儿子)、dep (深度) 这些信息。
int sz[maxn], fa[maxn], son[maxn], dep[maxn], b[maxn];
void dfs1(int u, int pre, int d) {
sz[u] = 1, fa[u] = pre, dep[u] = d;
int t = -1, v;
for(int i = head[u]; i; i = e[i].nxt) {
v = e[i].v;
// 有时需要边权压点权，就需要b[v] = e[i].w
dfs1(v, u, d + 1);
sz[u] += sz[v];
if(sz[v] > t) t = sz[v], son[u] = v;
}
}
第二次，处理 top (重链链顶)、dfn (dfs序，即通过dfs遍历得到的顺序)。
int top[maxn], dfn[maxn], cdf, a[maxn];
void dfs2(int u, int t) {
top[u] = t, dfn[u] = ++cdf, a[cdf] = b[u]; //b是原来的点权
if(son[u]) dfs2(son[u], t); //重儿子继续以当前链顶为顶，构成重链
int v;
for(int i = head[u]; i; i = e[i].nxt) {
v = e[i].v;
if(!dfn[v]) dfs2(v, v); //轻儿子以自己为顶，开辟一条新链
}
}
如此，我们就可以得到如下图被分割的树（每一个红色的圈就是重链，可以发现跳 \(\text log\) 次基本上就可以跳到任意另一个点）：
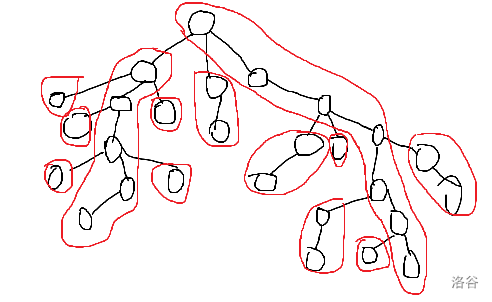
这样有什么用呢？我们可以极其快速地求任意两个点的LCA（最近公共祖先），只需要不停地向上跳重链的链顶，直到跳到同一条链即可：
LCA
int LCA(int x, int y) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y); //一定要让链顶深度更深的先跳上去，否则可能跳到更上方，就不是最近公共祖先了
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y); //深度更小的点就是LCA
return x;
}
当然，我们还能以dfs序（也可以叫dfn时间戳）为顺序，重新存一遍每个节点的信息，这样就能把树上问题转换为线性问题了，为什么呢？图解：
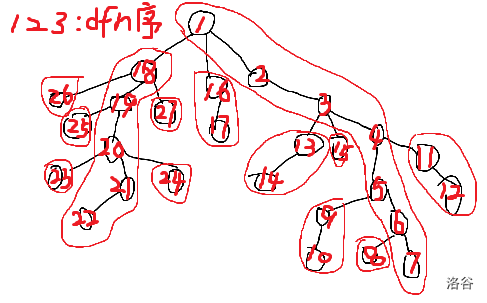
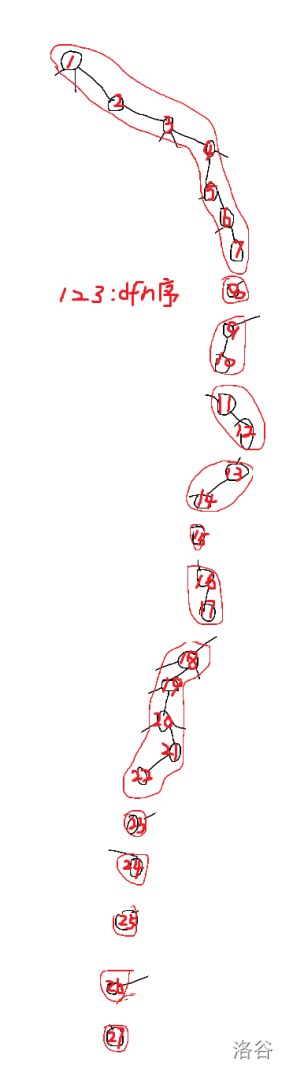
可以发现，按dfs序排序后，\([dfn[u],dfn[u]+size[u]-1]\) 这一个区间就是以u为根的子树，而对 \([dfn[top[u]], u]\) 这个区间进行操作，就可以实现对链的修改，又结合之前求LCA的方法，我们就能对树上的路径、子树进行区间操作，可以用线段树维护，时间复杂度\(O(\text log_n)\)
大段代码警告
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int N, M, R, P;
void read(int &x) {
x = 0; int f = 1; char c = getchar();
for(; !isdigit(c); c = getchar()) if(c == '-') f = -1;
for(; isdigit(c); c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
x *= f;
}
void write(int x) {
if(x < 0) putchar('-'), x = -x;
if(x > 9) write(x / 10);
putchar(x % 10 + 48);
}
struct edge {
int u, v, nxt;
} e[maxn << 1];
int head[maxn], ce;
void add(int u, int v) {
e[++ce] = {u, v, head[u]}; head[u] = ce;
}
int dep[maxn], sz[maxn], fa[maxn], son[maxn], top[maxn], dfn[maxn], a[maxn], b[maxn], cdf;
void dfs1(int u, int p, int d) {
sz[u] = 1, fa[u] = p, dep[u] = d;
int v, t = -1;
for(int i = head[u]; i; i = e[i].nxt) {
v = e[i].v;
if(v == p) continue;
dfs1(v, u, d + 1);
sz[u] += sz[v];
if(sz[v] > t) t = sz[v], son[u] = v;
}
}
void dfs2(int u, int t) {
top[u] = t, dfn[u] = ++cdf, a[cdf] = b[u];
if(son[u]) dfs2(son[u], t);
int v;
for(int i = head[u]; i; i = e[i].nxt) {
v = e[i].v;
if(!dfn[v]) dfs2(v, v);
}
}
//树剖
struct SegmentTree {
int l, r, sz, sum, lz;
} T[maxn << 2];
#define ls p << 1
#define rs p << 1 | 1
void up(int p) {
T[p].sum = T[ls].sum + T[rs].sum;
}
void build(int l, int r, int p) {
T[p].l = l, T[p].r = r, T[p].sz = r - l + 1, T[p].sum = 0, T[p].lz = 0; //一定要赋初值，符合周礼（事实上是为了多测清空）
if(l == r) {
T[p].sum = a[l] % P;
return;
}
int mid = l + r >> 1;
build(l, mid, ls); build(mid + 1, r, rs);
up(p);
}
#define mid T[p].l + T[p].r >> 1
void down(int p) {
T[ls].sum = (T[ls].sum + T[ls].sz * T[p].lz) % P; T[rs].sum = (T[rs].sum + T[rs].sz * T[p].lz) % P;
T[ls].lz = (T[ls].lz + T[p].lz) % P; T[rs].lz = (T[rs].lz + T[p].lz) % P;
T[p].lz = 0;
}
#define IntervalCheck l <= T[p].l and T[p].r <= r
void IntervalAdd(int l, int r, int c, int p) {
if(IntervalCheck) {
T[p].sum = (T[p].sum + T[p].sz * c) % P; T[p].lz = (T[p].lz + c) % P;
return;
}
down(p); //一定不要忘了pushdown！
if(l <= mid) IntervalAdd(l, r, c, ls);
if(r > mid) IntervalAdd(l, r, c, rs);
up(p);
}
int IntervalSum(int l, int r, int p) {
int ans = 0;
if(IntervalCheck) return T[p].sum;
down(p);
if(l <= mid) ans = (ans + IntervalSum(l, r, ls)) % P;
if(r > mid) ans = (ans + IntervalSum(l, r, rs)) % P;
up(p);
return ans;
}
//线段树
void TreeAdd(int x, int y, int c) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
IntervalAdd(dfn[top[x]], dfn[x], c, 1);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
IntervalAdd(dfn[x], dfn[y], c, 1);
}
int TreeSum(int x, int y) {
int ans = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
ans = (ans + IntervalSum(dfn[top[x]], dfn[x], 1)) % P;
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x, y);
ans = (ans + IntervalSum(dfn[x], dfn[y], 1)) % P;
return ans;
}
//跳链
int main() {
read(N), read(M), read(R), read(P);
for(int i = 1; i <= N; i++) read(b[i]);
for(int i = 1; i < N; i++) {
int u, v; read(u), read(v);
add(u, v); add(v, u);
}
dfs1(R, -1, 1); dfs2(R, R); build(1, N, 1);
while(M--) {
int op, x, y, z; read(op);
switch(op) {
case 1: read(x), read(y), read(z), TreeAdd(x, y, z); break;
case 2: read(x), read(y), write(TreeSum(x, y)); puts(""); break;
case 3: read(x), read(z), IntervalAdd(dfn[x], dfn[x] + sz[x] - 1, z, 1); break;
case 4: read(x), write(IntervalSum(dfn[x], dfn[x] + sz[x] - 1, 1)); puts(""); break;
}
}
} //128行，很符合OIer的XP
题目：
