AES学习记录
作者:@cryglz
本文为作者原创,转载请注明出处:https://www.cnblogs.com/Cryglz/p/17459438.html
很久之前就开始搞AES方面的,但都不是很懂,这次重新学习整理下
一.AES密码背景
AES的全称是Advanced Encryption Standard,意思是高级加密标准。它的出现主要是为了取代DES加密算法的,因为我们都知道DES算法的密钥长度是56Bit,因此算法的理论安全强度是2的56次方。但二十世纪中后期正是计算机飞速发展的阶段,元器件制造工艺的进步使得计算机的处理能力越来越强,虽然出现了3DES的加密方法,但由于它的加密时间是DES算法的3倍多,64Bit的分组大小相对较小,所以还是不能满足人们对安全性的要求。于是1997年1月2号,美国国家标准技术研究所宣布希望征集高级加密标准,用以取代DES。AES也得到了全世界很多密码工作者的响应,先后有很多人提交了自己设计的算法。最终有5个候选算法进入最后一轮:Rijndael,Serpent,Twofish,RC6和MARS。最终经过安全性分析、软硬件性能评估等严格的步骤,Rijndael算法获胜。此算法将成为美国新的数据加密标准而被广泛应用在各个领域中,AES作为新一代的数据加密标准汇聚了强安全性、高性能、高效率、易用和灵活等优点。其几乎能抵御所有已知的攻击,且在各种平台上都易于实现,速度快。二.AES的基本原理
AES为分组密码,分组密码也就是把明文分成一组一组的,每组长度相等,每次加密一组数据,直到加密完整个明文。在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的长度可以使用128位、192位或256位。密钥的长度不同,推荐加密轮数也不同。
AES算法主要有四种操作处理,分别是密钥加法层(也叫轮密钥加,英文Add Round Key)、字节代换层(SubByte)、行位移层(Shift Rows)、列混淆层(Mix Column)。而明文x和密钥k都是由16个字节组成的数据(当然密钥还支持192位和256位的长度,暂时不考虑),它是按照字节的先后顺序从上到下、从左到右进行排列的。而加密出的密文读取顺序也是按照这个顺序读取的,相当于将数组还原成字符串的模样了,然后再解密的时候又是按照4·4数组处理的。AES算法在处理的轮数上只有最后一轮操作与前面的轮处理上有些许不同(最后一轮只是少了列混淆处理),在轮处理开始前还单独进行了一次轮密钥加的处理。在处理轮数上,我们只考虑128位密钥的10轮处理。接下来,就开始一步步的介绍AES算法的处理流程了。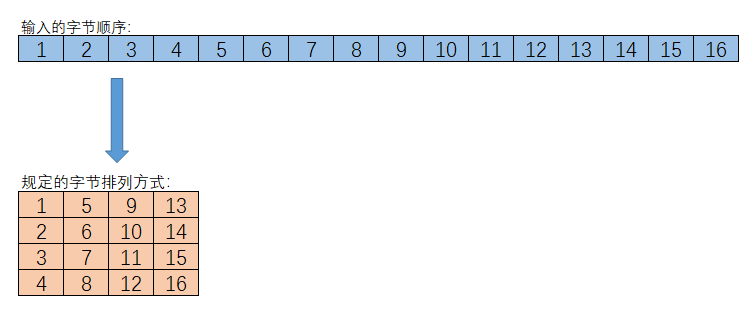
AES算法流程图
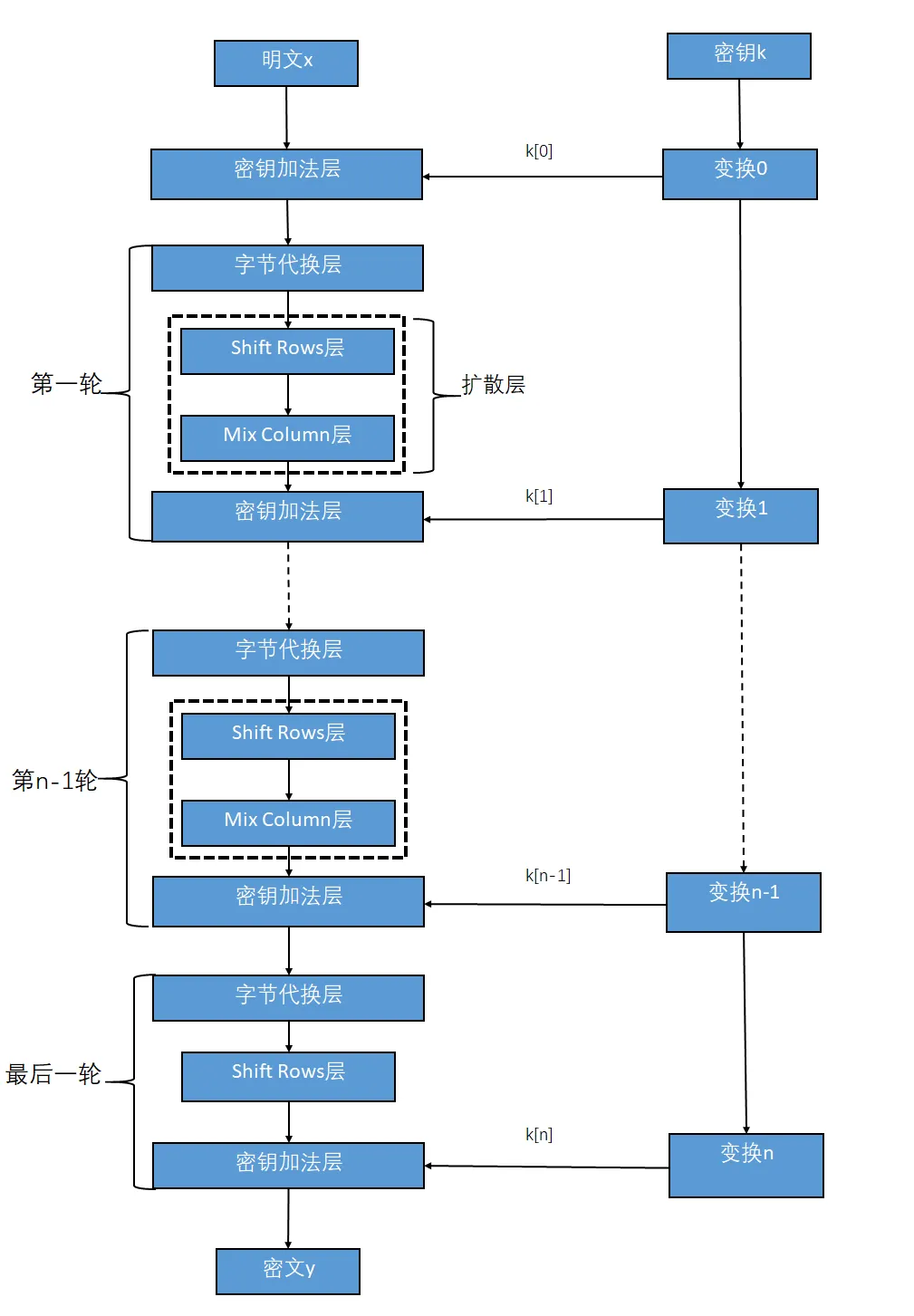
AES加密过程
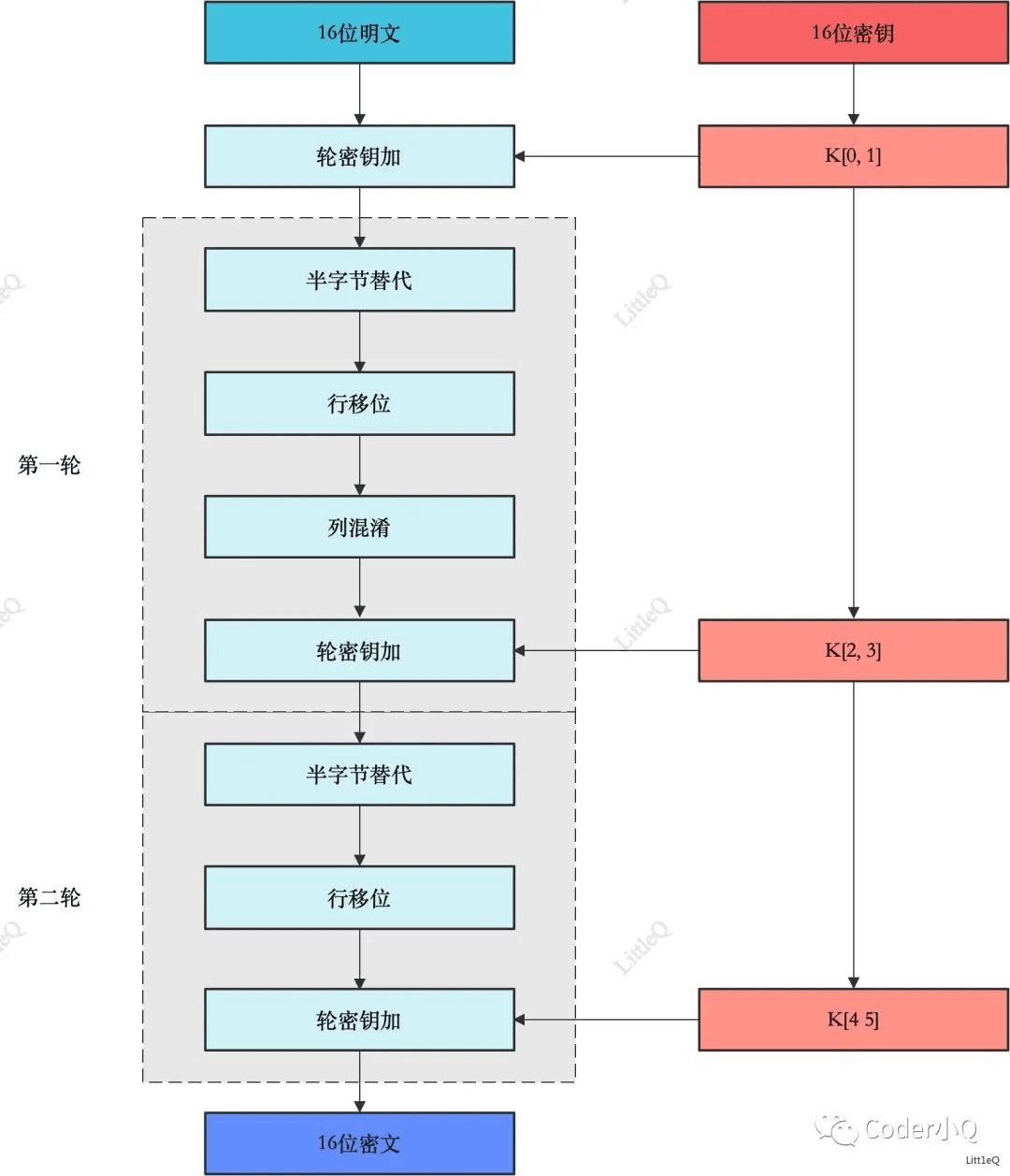
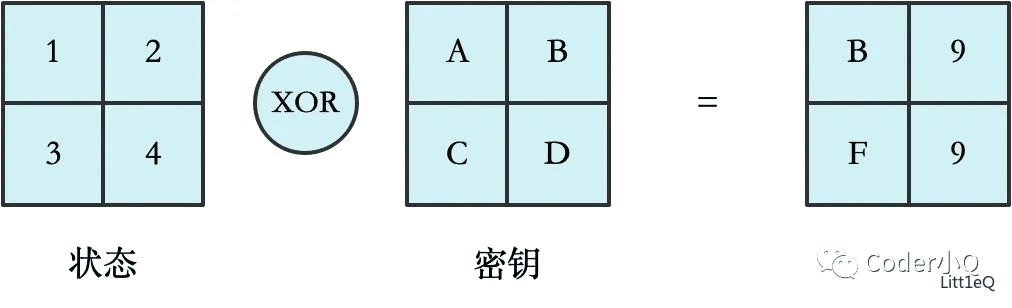
1.轮密钥加
在密钥加法层中有两个输入的参数,分别是明文和子密钥k[0],而且这两个输入都是128位的。k[0]实际上就等同于密钥k,具体原因在密钥生成中进行介绍。这一步比较简单,就是分别将各个状态和密钥进行异或操作,由于异或操作的可逆性,因此加密和解密过程当中的轮密钥加步骤是完全相同的。
2.字节代换
字节代替的主要功能是通过S盒完成一个字节到另外一个字节的映射。AES的字节代换其实就是一个简单的查表操作,定义了一个S盒和一个逆S盒:
s盒: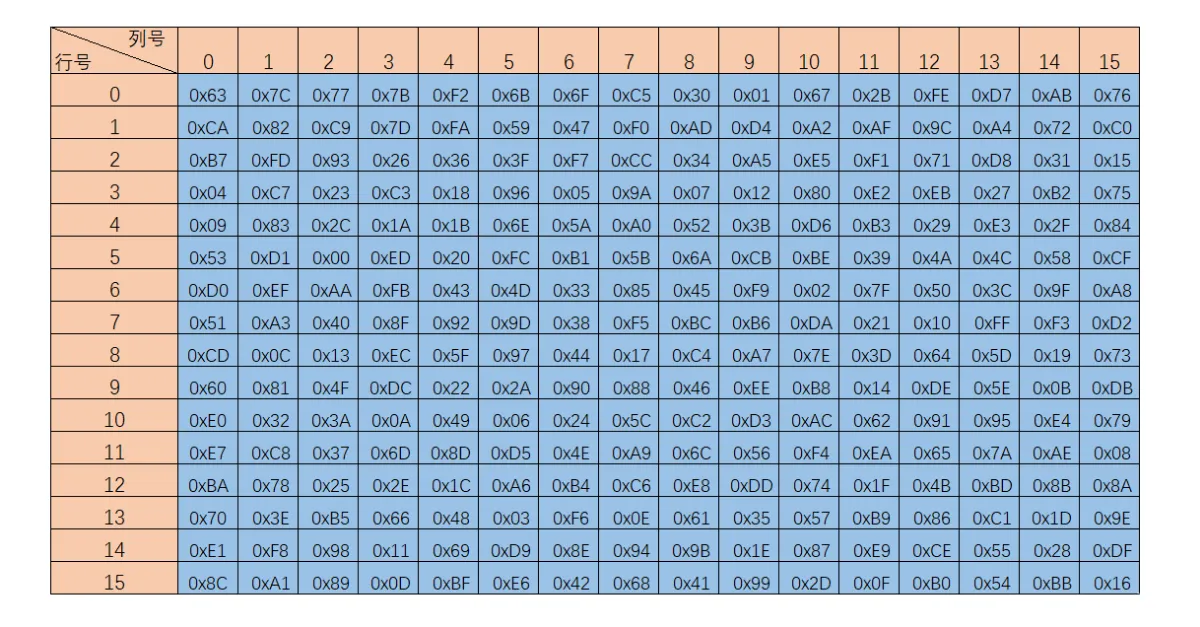
逆s盒: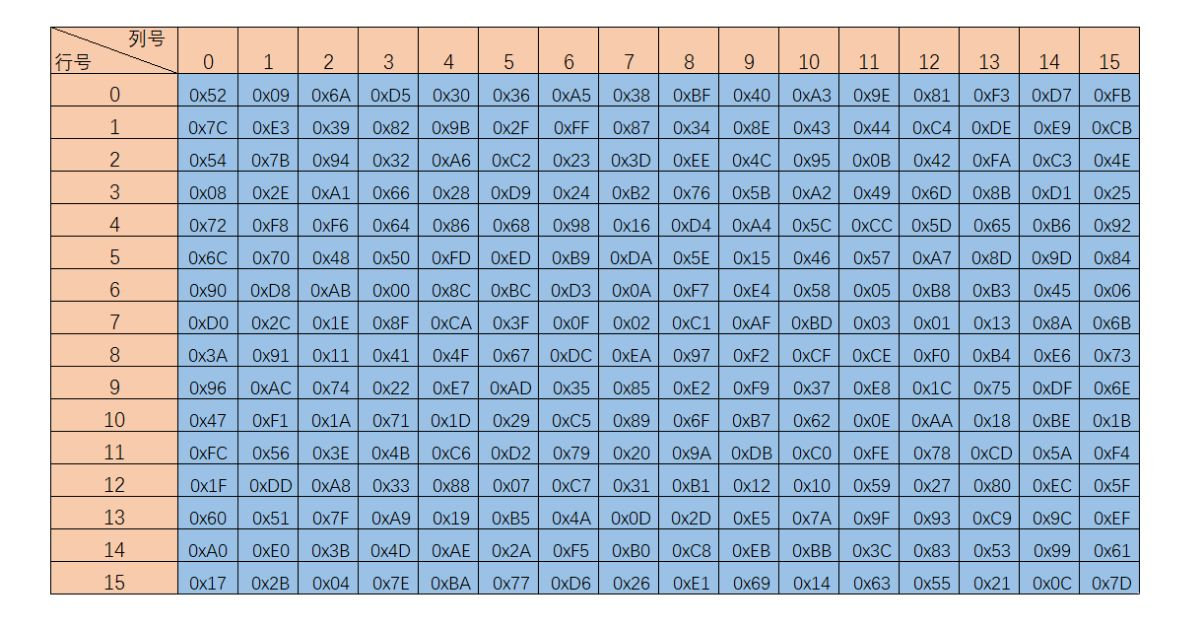
这一步操作是半个字的前半部分(二进制)作为行号,后半部分作为列号,以1(0001)为例,可以找到(00, 01), 查表即可得到对应的结果4:

逆操作也是一样,例如:字节00000000B替换后的值为(S[0][0]=)63H,再通过S-1即可得到替换前的值,(S-1 [6][3]=)00H。
加密图示: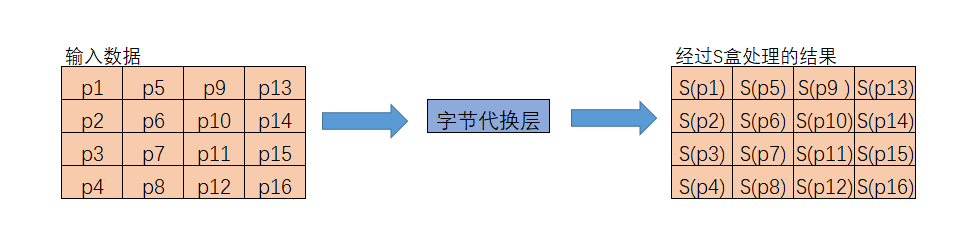
3.行移位
这一步对于AES来说,实际上也就是将第二行的两个元素换一下位置,原始操作应该是将第二行循环移动半个字。
它是用来将输入数据作为一个4·4的字节矩阵进行处理的,然后将这个矩阵的字节进行位置上的置换。ShiftRows子层属于AES手动的扩散层,目的是将单个位上的变换扩散到影响整个状态当,从而达到雪崩效应。在加密时行位移处理与解密时的处理相反,我们这里将解密时的处理称作逆行位移。它之所以称作行位移,是因为它只在4·4矩阵的行间进行操作,每行4字节的数据。在加密时,保持矩阵的第一行不变,第二行向左移动8Bit(一个字节)、第三行向左移动2个字节、第四行向左移动3个字节。而在解密时恰恰相反,依然保持第一行不变,将第二行向右移动一个字节、第三行右移2个字节、第四行右移3个字节。操作结束!

4.列混淆
AES算法中最为复杂的部分,属于扩散层,列混淆操作是AES算法中主要的扩散元素,它混淆了输入矩阵的每一列,使输入的每个字节都会影响到4个输出字节。行位移子层和列混淆子层的组合使得经过三轮处理以后,矩阵的每个字节都依赖于16个明文字节成可能。其中包含了矩阵乘法、伽罗瓦域内加法和乘法的相关知识。
列混合变换是通过矩阵相乘来实现的,经行移位后的状态矩阵与固定的矩阵相乘,得到混淆后的状态矩阵,如下图的公式所示:
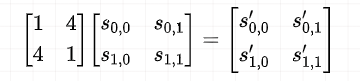
对与逆列混淆来说,其实就是找到一个矩阵使得这个矩阵乘以上面的矩阵等于一个二阶单位阵,因此列混淆的求逆操作如下:
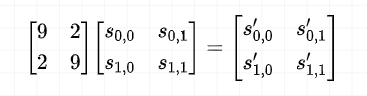
可以发现:

密钥扩展
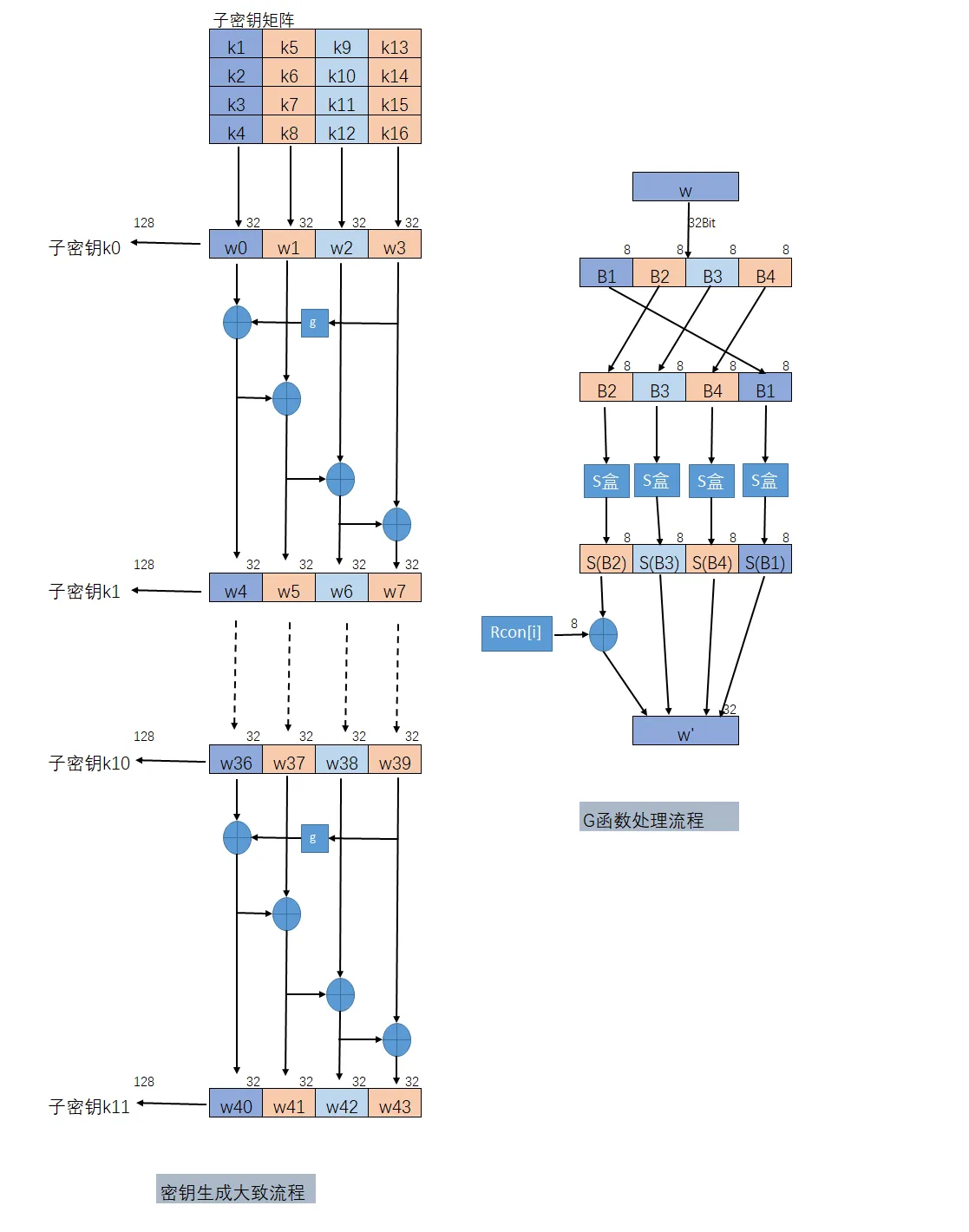
密钥扩展过程说明:
-
将种子密钥按图(a)的格式排列,其中k0、k1、……、k15依次表示种子密钥的一个字节;排列后用4个32比特的字表示,分别记为w[0]、w[1]、w[2]、w[3];
-
按照如下方式,依次求解w[j],其中j是整数并且属于[4,43];
-
若j%4=0,则w[j]=w[j-4]⊕g(w[j-1]),否则w[j]=w[j-4]⊕w[j-1];
函数g的流程说明:
a) 将w循环左移8比特;
b) 分别对每个字节做S盒置换;
c) 与32比特的常量(RC[j/4],0,0,0)进行异或,RC是一个一维数组,其值如下。(RC的值只需要有10个,而此处用了11个,实际上RC[0]在运算中没有用到,增加RC[0]是为了便于程序中用数组表示。由于j的最小取值是4,j/4的最小取值则是1,因此不会产生错误。)
RC = {0x00,0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36}
AES解密过程
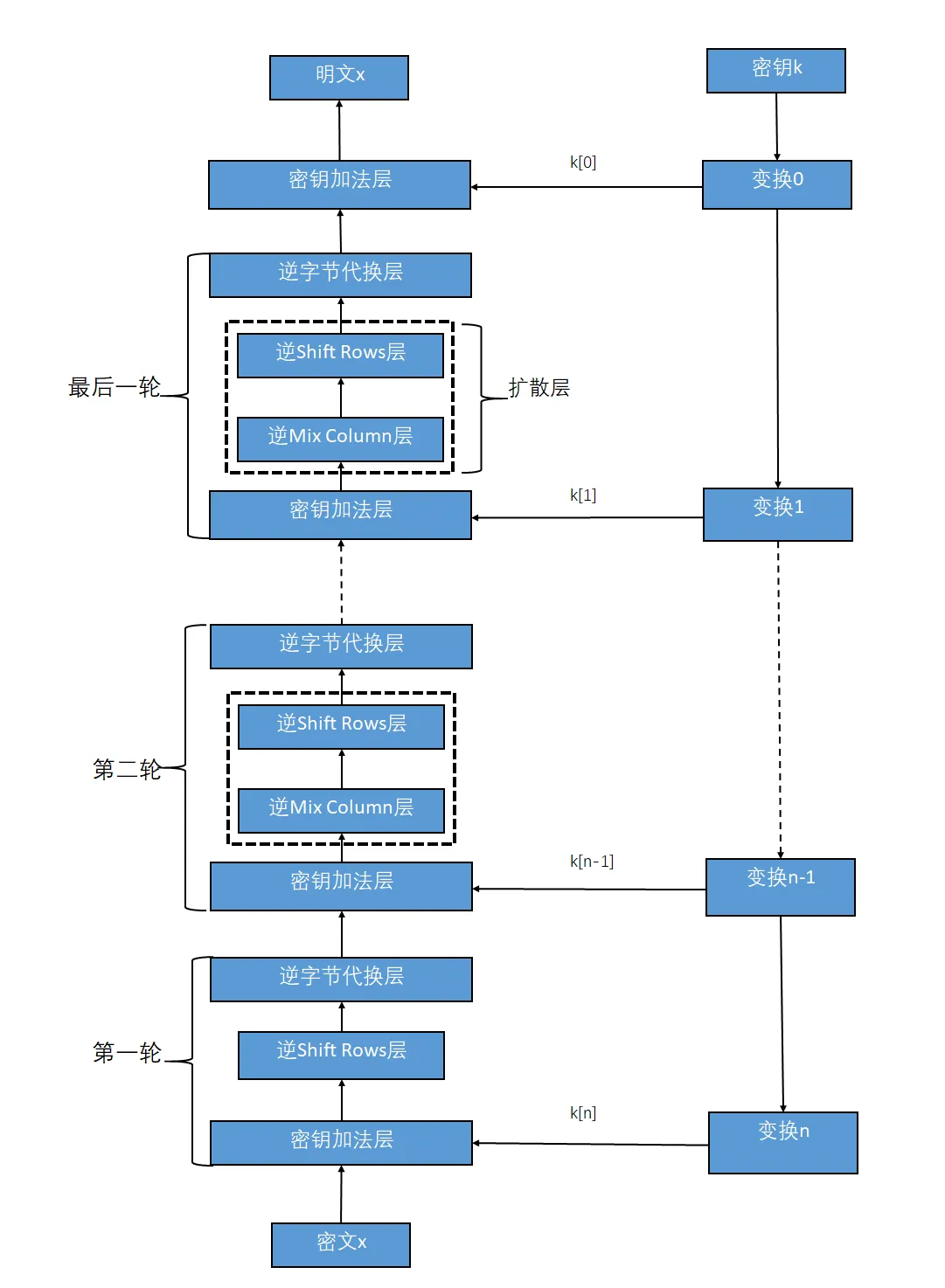
------------------------------------------------------分割线-------------------------------------------------------------------------
继续上次的学习,在学习AES时(也是密码学不可缺少的)绕不过的概念:
1.域(Fields)
在抽象代数中,“域”是一种可在其上进行加、减、乘和除运算而结果不会超自身的集合(代数结构),其概念是数域以及四则运算的推广。域是环的一种,其区别在于域要求它的元素可以进行除法运算,这等价于每个非零的元素都要有乘法逆元;同时,域中元素关于乘法是可交换的。一句话,域是乘法可交换的除环。
即:
1.若数集P中任意两数作某一运算的结果仍在P中,则称P对这个运算是封闭的。
2.数域的等价定义:如果一个包含0、1在内的数集P,对于加、减、乘、除(除数不为0)是封闭的,则称P为一个数域。
常见数域:复数域C;实数域R;有理数域Q(注意:自然数集N及整数集Z都不是数域,因为部分除法运算不是封闭的)。
2.有限域(伽罗华域Galois Fields)
①有限域定义
若域F只包含有限个元素,则称其为“有限域”,又称“伽罗华域”(由伽罗瓦(Galois.E)于18世纪30年代研究代数方程根式求解问题时引出的)。有限域在近代编码、计算机理论、组合数学等各方面有着广泛的应用。
有限域中元素的个数称为有限域的“阶”。阶必为素数的幂(如何证明?),可表示为p^n(p是素数、n∈Z+),这个素数P就是该有限域的“特征数”,通常用GF(pⁿ)表示pⁿ元的有限域。尽管存在有无限个元素的无限域,但只有有限域在密码编码学中得到了广泛的应用。元素个数相同的有限域是同构的。GF(pⁿ)的乘法群是(pⁿ-1)阶的循环群。
在密码学中,最常用的域是阶为p的素数域GF(p)或阶为2n的GF(2n)域。当n=1时,存在有限域GF(p),也称为“素数域”。GF(p)就是mod p,因为一个数模p后,结果在[0,p-1]之间,即该域中有p个元素;对于元素a和b,则(a+b) mod p和(a*b)mod p,其结果都是域中的元素;GF(p)里面的加法和乘法都是平时用的加法和乘法,GF(p)的加法和乘法单位元分别是0和1。
为什么p一定要是一个素数呢?这是因为当p为素数时,才能保证集合中的所有元素都有加法和乘法逆元(0除外)。假如p等于10,尽管所有元素都有加法逆元,但乘法不行,如元素2,因为找不到一个数a,使得2*a mod 10等于1;若p为素数,那么它就能保证域中的所有元素都有逆元。利用反证法和余数的定义即可证明。

有限域中最直观的例子就是阶为素数的域,即m=p^n(n=1)的域,域中的元素可以用整数
{0,1,.........,p-1} 来表示。
有限域有时也称伽罗瓦域,它指的是由有限个元素组成的集合,在这个集合内可以执行加、减、乘和逆运算。而在密码编码学中,我们只研究拥有有限个元素的域,也就是有限域。域中包含元素的个数称为域的阶。只有当m是一个素数幂时,即m=pn(其中n为正整数是p的次数,p为素数),阶为m的域才存在。p称为这个有限域的特征。也就是说,有限域中元素的个数可以是11(p=11是一个素数,n=1)、可以是81(p=3是一个素数,n=4)、也可以是256(p=2是一个素数,n=8).....但有限域的中不可能拥有12个元素,因为12=2·2·3,因此12也不是一个素数幂。有限域中最直观的例子就是阶为素数的域,即n=1的域。的元素可以用整数0、1、...、p-1l来表示。域的两种操作就是模整数加法和整数乘法模p。加上p是一个素数,整数环Z表示为GF(p),也成为拥有素数个元素的素数域或者伽罗瓦域。GF(p)中所有的非零元素都存在逆元,GF(p)内所有的运算都是模p实现的。
素域内的算数运算规则如下:
(1)加法和乘法都是通过模p实现的;
(2)任何一个元素a的加法逆元都是由a+(a的逆元)=0 mod p得到的;
(3)任何一个非零元素a的乘法逆元定义为a·a的逆元=1。
例:在素域GF(5)={0、1、2、3、4}中,2的加法逆元为3,这是因为2+(3)=5,5mod5=0,所以2+3=5mod5=0。2的乘法逆元为3,这是因为2·3=6,6mod5=1,所以2·3=6mod5=1。(在很多地方a的加法逆元用-a表示,a的乘法逆元用1/a表示)
注:GF(2)是一个非常重要的素域,也是存在的最小的有限域,由于GF(2)的加法,即模2加法与异或(XOR)门等价,GF(2)的乘法与逻辑与(AND)门等价,所以GF(2)对AES非常重要。
扩展域:
如果有限域的阶不是素数,则这样的有限域内的加法和乘法运算就不能用模整数加法和整数乘法模p表示。而且m>1的域被称为扩展域,为了处理扩展域,我们就要使用不同的符号表示扩展域内的元素,使用不同的规则执行扩展域内元素的算术运算。
在扩展域GF(2m)中,元素并不是用整数表示的,而是用系数为域GF(2)中元素的多项式表示。这个多项式最大的度(幂)为m-1,所以每个元素共有m个系数,在AES算法使用的域GF(28)中,每个元素A∈GF(28)都可以表示为:
注意:在域GF(28)中这样的多项式共有256个,这256个多项式组成的集合就是扩展域GF(28)。每个多项式都可以按一个8位项链的数值形式存储:
像x7、x6等因子都无需存储,因为从位的位置就可以清楚地判断出每个系数对应的幂。
扩展域GF(2m)内的加减法:
在AES算法中的密钥加法层中就使用了这部分的知识,但是不是很明显,因为我们通常把扩展域中的加法当作异或运算进行处理了,因为在扩展域中的加减法处理都是在底层域GF(2)内完成的,与按位异或运算等价。
注:在减法运算中减号之所以变成加号,这就和二进制减法的性质有关了。从上述两个公式中我们发现在扩展域中加法和减法等价,并且与XOR等价(异或运算也被称作二进制加法)。
扩展域的乘法主要运用在AES算法的列混淆层(Mix Column)中,也是列混淆层中最重要的操作。我们项要将扩展域中的两个元素用多项式形式展开,然后使用标准的多项式乘法规则将两个多项式相乘:
注:通常在多项式乘法中C(x)的度会大于m-1,因此需要对此进行化简,而化简的基本思想与素域内乘法情况相似:在素域GF(p)中,将两个整数相乘得到的结果除以一个素数,化简后的结果就是最后的余数。而在扩展域中进行的操作就是:将两个多项式相乘的结果除以一个不可约多项式,最后的结果就是最后的余数。(这里的不可约多项式大致可以看作一个素数)

-----------------------------------------------------分割线--------------------------------------------------------------------



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异
· 三行代码完成国际化适配,妙~啊~