cryptohack wp （MATHEMATICS篇）（持续更新）

还是那句话，本篇中未提及的题目均在sources的其他篇目

Vectors

算向量点积，题目中也介绍了点积的计算，直接给代码：

import numpy as np

v = np.array([2, 6, 3])
w = np.array([1, 0, 0])
u = np.array([7, 7, 2])

result = np.dot(3 * (2 * v - w), 2 * u) #np.dot:计算向量的点积

print(result)

Size and Basis

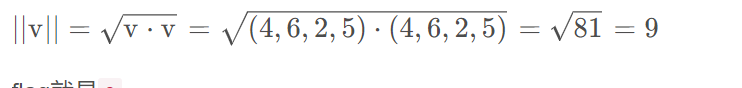
代码如下：

import math

v = [4, 6, 2, 5]

size = math.sqrt(sum([x**2 for x in v]))

print(size)

Gram Schmidt

我这里直接用的chatgpt给出的代码：

import numpy as np

# Given basis vectors
v1 = np.array([4, 1, 3, -1])
v2 = np.array([2, 1, -3, 4])
v3 = np.array([1, 0, -2, 7])
v4 = np.array([6, 2, 9, -5])

# Apply Gram-Schmidt algorithm
u1 = v1
u2 = v2 - np.dot(v2, u1) / np.linalg.norm(u1)**2 * u1
u3 = v3 - np.dot(v3, u1) / np.linalg.norm(u1)**2 * u1 - np.dot(v3, u2) / np.linalg.norm(u2)**2 * u2
u4 = v4 - np.dot(v4, u1) / np.linalg.norm(u1)**2 * u1 - np.dot(v4, u2) / np.linalg.norm(u2)**2 * u2 - np.dot(v4, u3) / np.linalg.norm(u3)**2 * u3
``
# Extract the flag (second component of u4)
flag = u4[1]

# Print the flag value rounded to 5 significant figures
print(round(flag, 5))

What’s Lattice?

sage直接解：
sage: v = vector
sage: v1 = v([6,2,-3])
sage: v2 = v([5,1,4])
sage: v3 = v([2,7,1])
sage: A = matrix([v1,v2,v3])
sage:det(A)

---------------------------------------------------------分割线---------------------------------------------------------------

Gaussian Reduction

如果你仔细观察，“格”开始出现在密码学中的每一个角落。 有时它们操纵一个加密系统，破坏了(生成)不够安全的参数。 最著名的例子是 Coppersmith 对 RSA 加密的攻击。

格也可用于构建加密协议，其安全性基于两个基本的“难”问题：

The Shortest Vector Problem (SVP)
给定的基向量和格，找到格L LL中的长度最短非零向量。换言之，找到一个非零向量v ∈ L v\in Lv∈L使 ∣ ∣ v ∣ ∣ ||v||∣∣v∣∣ 最小

The Closest Vector Problem (CVP)
给定的基向量、格，和一个不在格上的目标向量，找到距离目标向量最近的格向量。

给定一个不在格L LL中的向量w ∈ R m w\in R^mw∈R
m
，找到向量v ∈ L v\in Lv∈L使 ∣ ∣ v − w ∣ ∣ ||v-w||∣∣v−w∣∣ 最小

对于一般的格，SVP问题十分困难，但对于相对简单的情况，我们有非常有效的算法可以计算出问题的解或者近似解。当格的维数小于等于4时，可以在多项式时间内计算出确定解，对于更高维，只能求出近似解。

高斯发明了一种算法来找到给定任意基的二维格 L LL 的最佳基。算法的输出 v1 是 L LL 中最短的非零向量，由此解决了二维的SVP问题。

高斯的算法大致通过从另一个基向量中减去一个基向量的倍数来达到目标，直到不再可能使它们变得更小。这适用于二维，因此可以很好地可视化。

import numpy as np
ar = np.array
v = ar([846835985, 9834798552],dtype='i8')
u = ar([87502093, 123094980],dtype='i8')
v1,v2 = u,v

>>> if siz2(v2) < siz2(v1):
	print('swap')
	v1,v2 = v2,v1

>>> m = int(v1.dot(v2)/v1.dot(v1));m
56
>>> v2 = v2 - m*v1;v2
array([-4053281223,  2941479672], dtype=int64)
>>> if siz2(v2) < siz2(v1):
	print('swap')
	v1,v2 = v2,v1
	
>>> m = int(v1.dot(v2)/v1.dot(v1));m
0
>>> v1
array([ 87502093, 123094980], dtype=int64)
>>> v2
array([-4053281223,  2941479672], dtype=int64)
>>> v1.dot(v2)
7410790865146821

Find the Lattice

from Crypto.Util.number import getPrime, inverse, bytes_to_long
import random
import math

FLAG = b'crypto{?????????????????????}'
def gen_key():
    q = getPrime(512)
    upper_bound = int(math.sqrt(q // 2))
    lower_bound = int(math.sqrt(q // 4))
    f = random.randint(2, upper_bound)
    while True:
        g = random.randint(lower_bound, upper_bound)
        if math.gcd(f, g) == 1:
            break
    h = (inverse(f, q)*g) % q
    return (q, h), (f, g)

def encrypt(q, h, m):
    assert m < int(math.sqrt(q // 2))
    r = random.randint(2, int(math.sqrt(q // 2)))
    e = (r*h + m) % q
    return e

def decrypt(q, h, f, g, e):
    a = (f*e) % q
    m = (a*inverse(f, g)) % g
    return m


public, private = gen_key()
q, h = public
f, g = private

m = bytes_to_long(FLAG)
e = encrypt(q, h, m)

print(f'Public key: {(q,h)}')
print(f'Encrypted Flag: {e}')

---------------------------------------------------------分割线---------------------------------------------------------------

Backpack Cryptography

import random
from collections import namedtuple
import gmpy2
from Crypto.Util.number import isPrime, bytes_to_long, inverse, long_to_bytes

FLAG = b'crypto{??????????????????????????}'
PrivateKey = namedtuple("PrivateKey", ['b', 'r', 'q'])

def gen_private_key(size):
    s = 10000
    b = []
    for _ in range(size):
        ai = random.randint(s + 1, 2 * s)
        assert ai > sum(b)
        b.append(ai)
        s += ai
    while True:
        q = random.randint(2 * s, 32 * s)
        if isPrime(q):
            break
    r = random.randint(s, q)
    assert q > sum(b)
    assert gmpy2.gcd(q,r) == 1
    return PrivateKey(b, r, q)


def gen_public_key(private_key: PrivateKey):
    a = []
    for x in private_key.b:
        a.append((private_key.r * x) % private_key.q)
    return a


def encrypt(msg, public_key):
    assert len(msg) * 8 <= len(public_key)
    ct = 0
    msg = bytes_to_long(msg)
    for bi in public_key:
        ct += (msg & 1) * bi
        msg >>= 1
    return ct


def decrypt(ct, private_key: PrivateKey):
    ct = inverse(private_key.r, private_key.q) * ct % private_key.q
    msg = 0
    for i in range(len(private_key.b) - 1, -1, -1):
         if ct >= private_key.b[i]:
             msg |= 1 << i
             ct -= private_key.b[i]
    return long_to_bytes(msg)


private_key = gen_private_key(len(FLAG) * 8)
public_key = gen_public_key(private_key)
encrypted = encrypt(FLAG, public_key)
decrypted = decrypt(encrypted, private_key)
assert decrypted == FLAG

print(f'Public key: {public_key}')
print(f'Encrypted Flag: {encrypted}')

解题代码：

from Crypto.Util.number import long_to_bytes

p = '[-1  1 -1 -1 -1 -1 -1  1  1  1 -1  1 -1 -1 -1  1  1  1  1 -1  1 -1 -1  1 -1 -1 -1  1  1 -1 -1  1 -1  1  1  1 -1 -1  1  1 -1 -1  1  1 -1 -1  1  1 -1 -1 -1  1 -1 -1 -1  1  1  1 -1  1 -1 -1 -1  1  1  1  1 -1  1 -1 -1  1 -1 -1 -1  1  1 -1 -1  1 -1  1  1  1 -1 -1  1  1  1  1 -1 -1  1 -1 -1  1 -1 -1 -1 -1 -1  1 -1  1 -1 -1  1  1 -1 -1 -1  1 -1  1  1  1 -1 -1  1  1 -1 -1 -1 -1 -1  1 -1  1 -1 -1  1 -1  1 -1 -1  1 -1 -1  1  1  1 -1 -1  1  1  1 -1  1 -1 -1  1  1 -1 -1  1  1 -1 -1 -1  1  1  1  1  1 -1 -1 -1  1  1  1 -1  1 -1 -1  1  1  1 -1 -1 -1  1 -1 -1  1 -1 -1  1 -1  1 -1 -1  1 -1 -1 -1 -1 -1  1 -1  1 -1  1  1 -1 -1 -1 -1  1 -1  1 -1 -1  1 -1 -1  1 -1 -1  1 -1 -1 -1 -1  1 -1 -1 -1 -1  1 -1 -1  1  1  1 -1  1 -1 -1 -1  1  1  1  1  1 -1 -1 -1  1 -1  1  1 -1 -1 -1 -1  1  1 -1  1  1 -1 -1 -1  1 -1 -1  1  1  1 -1 -1  1  0]'
p = p.replace('  ', ',')
p = '[-1,1 -1 -1 -1 -1 -1,1,1,1 -1,1 -1 -1 -1,1,1,1,1 -1,1 -1 -1,1 -1 -1 -1,1,1 -1 -1,1 -1,1,1,1 -1 -1,1,1 -1 -1,1,1 -1 -1,1,1 -1 -1 -1,1 -1 -1 -1,1,1,1 -1,1 -1 -1 -1,1,1,1,1 -1,1 -1 -1,1 -1 -1 -1,1,1 -1 -1,1 -1,1,1,1 -1 -1,1,1,1,1 -1 -1,1 -1 -1,1 -1 -1 -1 -1 -1,1 -1,1 -1 -1,1,1 -1 -1 -1,1 -1,1,1,1 -1 -1,1,1 -1 -1 -1 -1 -1,1 -1,1 -1 -1,1 -1,1 -1 -1,1 -1 -1,1,1,1 -1 -1,1,1,1 -1,1 -1 -1,1,1 -1 -1,1,1 -1 -1 -1,1,1,1,1,1 -1 -1 -1,1,1,1 -1,1 -1 -1,1,1,1 -1 -1 -1,1 -1 -1,1 -1 -1,1 -1,1 -1 -1,1 -1 -1 -1 -1 -1,1 -1,1 -1,1,1 -1 -1 -1 -1,1 -1,1 -1 -1,1 -1 -1,1 -1 -1,1 -1 -1 -1 -1,1 -1 -1 -1 -1,1 -1 -1,1,1,1 -1,1 -1 -1 -1,1,1,1,1,1 -1 -1 -1,1 -1,1,1 -1 -1 -1 -1,1,1 -1,1,1 -1 -1 -1,1 -1 -1,1,1,1 -1 -1,1,0]'
p = p.replace(' ', ',')
# 处理p
# print(p)
p = [-1, 1, -1, -1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, -1, 1, -1, -1, 1, -1, -1, -1, 1, 1, -1, -1, 1,
     -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1,
     1, 1, -1, 1, -1, -1, 1, -1, -1, -1, 1, 1, -1, -1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, 1, -1, -1, 1, -1, -1,
     -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, -1, -1, -1, 1, -1, 1, -1, -1,
     1, -1, 1, -1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1,
     1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1, 1, -1, -1, -1,
     -1, -1, 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, -1, -1, 1, -1, -1,
     -1, -1, 1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1, 1, -1, 1,
     1, -1, -1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, 0]
# print(len(p))
p = [-1, 1, -1, -1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, -1, 1, -1, -1, 1, -1, -1, -1, 1, 1, -1, -1, 1,
     -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1,
     1, 1, -1, 1, -1, -1, 1, -1, -1, -1, 1, 1, -1, -1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, 1, -1, -1, 1, -1, -1, 1, -1, -1,
     -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, -1, -1, -1, 1, -1, 1, 1, 1, -1, -1, 1, 1, -1, -1, -1, -1, -1, 1, -1, 1, -1, -1,
     1, -1, 1, -1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, 1, -1, -1, -1, 1, 1, 1, 1,
     1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1, 1, -1, -1, -1,
     -1, -1, 1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, -1, -1, 1, -1, -1,
     -1, -1, 1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, 1, -1, -1, -1, 1, -1, 1, 1, -1, -1, -1, -1, 1, 1, -1, 1,
     1, -1, -1, -1, 1, -1, -1, 1, 1, 1, -1, -1, 1]
# 去掉最后一位的0
s = ''
# 这里是1表示二进制1，还是-1表示二进制0都有可能，两种试一下最后得到的密文正确就表示哪种正确
for i in p:
    if i == 1:
        s = '0' + s  # x1表示的是低位，所以应该一个一个往高位加
    else:
        s = '1' + s
p = '01100011011100100111100101110000011101000110111101111011011011010111100101011111011010110110111000110100011100000111001100110100011000110110101101011111001100010111001101011111011011000011000101100111011010000111010001110111001100110011000101100111011010000111010001111101'
print(long_to_bytes((int(p, 2))))