cryptohack wp （SYMMETRIC CRYPTOGRAPHY篇）（持续更新）

对称密码学

Keyed Permutations

"一对一对应"的数学术语是双射（bijection）。如果一个函数将其定义域中的每个元素映射到其值域中的唯一元素，并且反过来也是如此，那么该函数就被称为双射。在块密码的背景下，双射确保在使用特定密钥时，每个可能的输入块都映射到一个唯一的输出块，反之亦然。这种属性对于加密和解密过程的安全性和正确性至关重要。

Resisting Bruteforce

针对 AES 的最佳单密钥攻击的名称是 Biclique Cryptanalysis。这种攻击利用了AES加密过程中的特定性质，通过寻找两个具有特定关系的密文块，然后逆推它们的明文和密钥。它可以在$2^{{126.1}$的时间内破解AES-128，比理论上的$2}$的暴力破解时间复杂度快得多，因此被认为是对AES加密的威胁。Biclique Cryptanalysis可以看作是Differential Cryptanalysis和Linear Cryptanalysis的结合，并使用了它们的一些技术和工具。
flag:crypto{Biclique}

Structure of AES

def bytes2matrix(text):
    """ Converts a 16-byte array into a 4x4 matrix.  """
    return [list(text[i:i+4]) for i in range(0, len(text), 4)]

def matrix2bytes(matrix):
    """ Converts a 4x4 matrix into a 16-byte array.  """


def matrix2bytes(matrix):
    # 获取矩阵的行数和列数
    rows = len(matrix)
    cols = len(matrix[0])

    # 创建一个空列表
    result = []

    # 按列顺序将矩阵中的每个元素添加到字节数组中
    for i in range(cols):
        for j in range(rows):
            result.append(matrix[i][j])


    # 返回生成的字节数组
    return bytes(result)

# def matrix2bytes(matrix):
#     """ Converts a 4x4 matrix into a 16-byte array.  """
#     return bytes(sum(matrix, []))


matrix = [
    [99, 114, 121, 112],
    [116, 111, 123, 105],
    [110, 109, 97, 116],
    [114, 105, 120, 125],
]

print(matrix2bytes(matrix))
#crypto{inmatrix}

Round Keys

按照题目要求给出代码：

state = [
    [206, 243, 61, 34],
    [171, 11, 93, 31],
    [16, 200, 91, 108],
    [150, 3, 194, 51],
]

round_key = [
    [173, 129, 68, 82],
    [223, 100, 38, 109],
    [32, 189, 53, 8],
    [253, 48, 187, 78],
]


def add_round_key(s, k):
    """
    对状态矩阵 s 和轮密钥 k 进行异或运算，返回一个新的状态矩阵。
    """
    # 创建一个新的状态矩阵，初始化为零
    result = [[0] * 4 for _ in range(4)]

    # 对每个位置上的元素进行异或运算
    for i in range(4):
        for j in range(4):
            result[i][j] = s[i][j] ^ k[i][j]

    return result
def matrix2bytes(matrix):
#     """ Converts a 4x4 matrix into a 16-byte array.  """
     return bytes(sum(matrix, []))

print(matrix2bytes(add_round_key(state, round_key)))

Confusion through Substitution

AES中的字节代换这一部分，AES的SubBytes阶段使用一个由256个字节数组组成的S-box来进行字节代换。S-box的字节值是按照特定规则计算得出的，可以直接用于字节代换。在SubBytes阶段，输入状态矩阵中的每个字节都会被使用S-box中对应的字节值替换掉。
下面是解题代码：

s_box = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)

inv_s_box = (
    0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
    0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
    0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
    0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
    0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
    0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
    0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
    0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
    0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
    0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
    0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
    0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
    0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
    0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
    0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
    0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)

state = [
    [251, 64, 182, 81],
    [146, 168, 33, 80],
    [199, 159, 195, 24],
    [64, 80, 182, 255],
]


def sub_bytes(s, sbox=s_box):
    for i in range(4):
        for j in range(4):
            print(chr(sbox[s[i][j]]), end="")


print(sub_bytes(state, sbox=inv_s_box))

Diffusion through Permutation

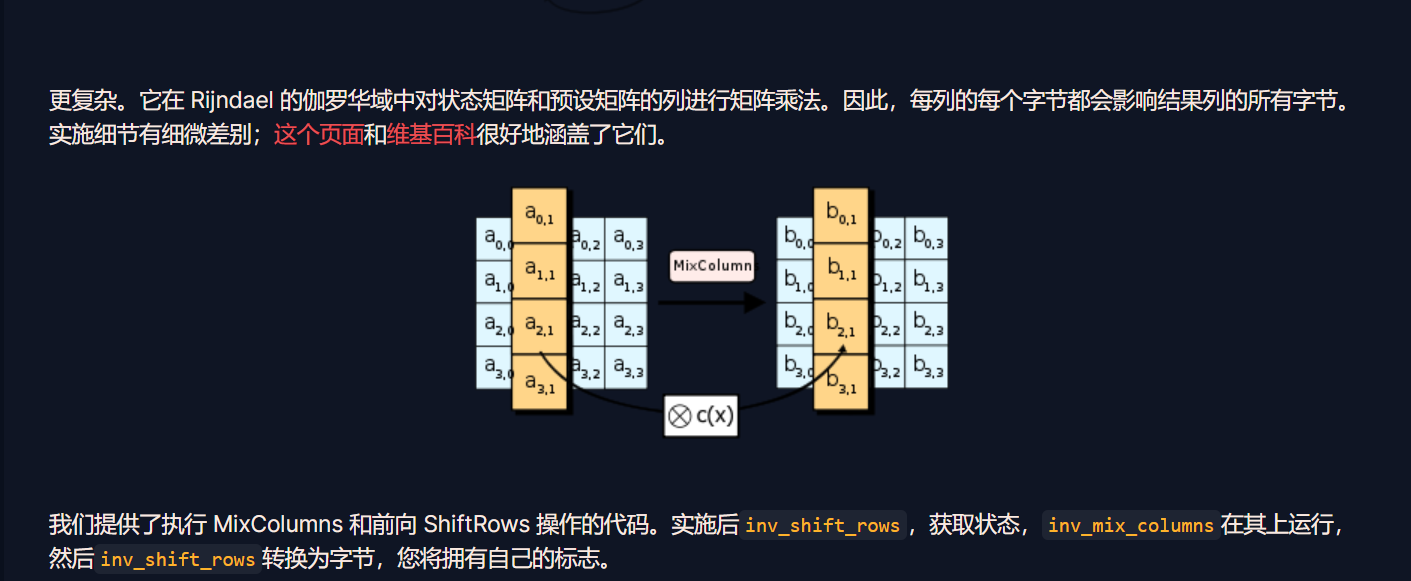
行变换：AES的行变换（ShiftRows）阶段用于对状态矩阵中的每一行进行循环移位变换。具体来说，第 0 行不变，第 1 行循环左移 1 个字节，第 2 行循环左移 2 个字节，第 3 行循环左移 3 个字节。这个行移位的过程可以看成是一个在状态矩阵的每一行中旋转字节的操作。
解题代码如下：

def shift_rows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]


def inv_shift_rows(s):
    s[1][1], s[2][1], s[3][1], s[0][1] = s[0][1], s[1][1], s[2][1], s[3][1]
    s[2][2], s[3][2], s[0][2], s[1][2] = s[0][2], s[1][2], s[2][2], s[3][2]
    s[3][3], s[0][3], s[1][3], s[2][3] = s[0][3], s[1][3], s[2][3], s[3][3]


# learned from http://cs.ucsb.edu/~koc/cs178/projects/JT/aes.c
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)


def mix_single_column(a):
    # see Sec 4.1.2 in The Design of Rijndael
    t = a[0] ^ a[1] ^ a[2] ^ a[3]
    u = a[0]
    a[0] ^= t ^ xtime(a[0] ^ a[1])
    a[1] ^= t ^ xtime(a[1] ^ a[2])
    a[2] ^= t ^ xtime(a[2] ^ a[3])
    a[3] ^= t ^ xtime(a[3] ^ u)


def mix_columns(s):
    for i in range(4):
        mix_single_column(s[i])


def inv_mix_columns(s):
    # see Sec 4.1.3 in The Design of Rijndael
    for i in range(4):
        u = xtime(xtime(s[i][0] ^ s[i][2]))
        v = xtime(xtime(s[i][1] ^ s[i][3]))
        s[i][0] ^= u
        s[i][1] ^= v
        s[i][2] ^= u
        s[i][3] ^= v

    mix_columns(s)


state = [
    [108, 106, 71, 86],
    [96, 62, 38, 72],
    [42, 184, 92, 209],
    [94, 79, 8, 54],
]

inv_mix_columns(state)
inv_shift_rows(state)
for i in range(4):
    for j in range(4):
        print(chr(state[i][j]), end="")