cryptohack wp （MODULAR ARITHMETIC篇）

第二节模运算----第一题（ GCD ）

在做这道题前，了解下欧几里得算法：
欧几里得算法，也叫辗转相除法，用于求解两个非负整数a和b的最大公约数（Greatest Common Divisor, GCD），即能够同时整除它们的最大正整数。

算法的基本思想是，通过不断求解a和b的余数的最大公约数，最终可以得到a和b的最大公约数。

具体地，设r为a除以b的余数，则有：

a = bq + r

其中，q为a除以b的商。如果r等于0，则b就是a和b的最大公约数；否则，继续使用同样的方法求解b和r的最大公约数。直到r等于0为止，此时的b就是a和b的最大公约数

以下是Python实现该算法的代码：

a = 66528
b = 52920

def gcd(a, b):  #欧几里得算法
    if b == 0:
        return a
    else:
        return gcd(b, a % b)
    
print(gcd(a,b))

第二题（Extended GCD）

在进行这道题之前，先了解下扩展欧几里得算法吧：
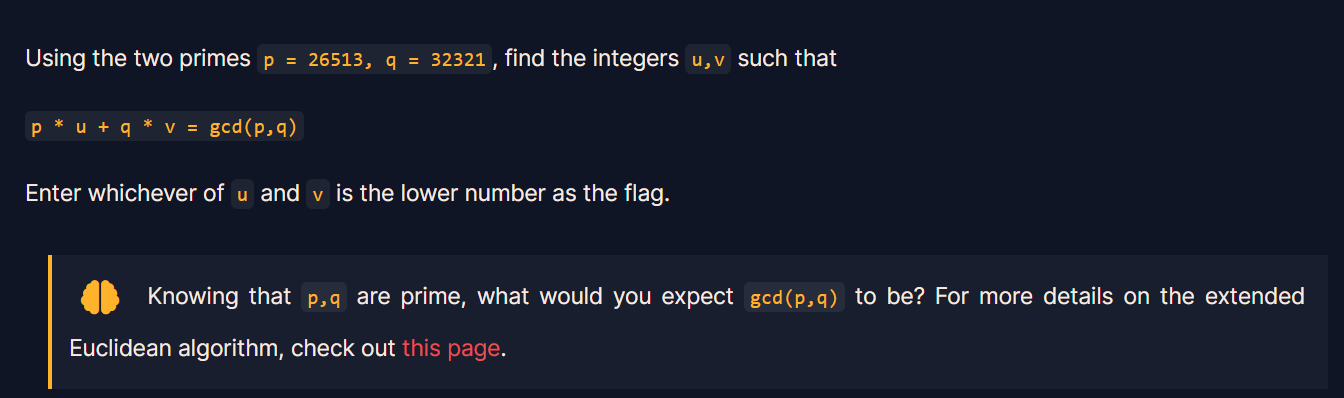
扩展欧几里得算法是求解两个整数a、b的最大公约数（Greatest Common Divisor, GCD）以及一组整数x、y，使得它们满足以下等式：
ax + by = gcd(a,b)
其中，x、y是整数，gcd(a,b)表示a、b的最大公约数。
该算法的基本思想是利用欧几里得算法递归求解gcd(a,b)，并在递归的过程中同时求解x、y的值。
具体地，假设我们已经求得了b和a%b（即a除以b的余数）的最大公约数gcd(b, a%b)，并得到了一组整数x1、y1，使得：
bx1 + (a%b)y1 = gcd(b, a%b)
接下来，我们可以将a%b表示为a-b(a//b)，其中a//b表示a除以b的商，将其带入上式得：
bx1 + (a - b(a//b))y1 = gcd(b, a%b)
移项可得：
ay1 + b(x1 - (a//b)y1) = gcd(b, a%b)
由此可以得到a和b的最大公约数gcd(a,b)和一组整数x、y，使得：
ax + by = gcd(a,b)
其中：
gcd(a,b) = gcd(b, a%b)
x = y1
y = x1 - (a//b)*y1

最终的结果是递归求解出gcd(a,b)的同时求得了x和y的值。
以下是python代码实现：

def egcd(a, b):  #扩展欧几里得算法
    if b == 0:
        return (a, 1, 0)
    else:
        gcd, x1, y1 = egcd(b, a % b)
        x = y1
        y = x1 - (a // b) * y1
        return (gcd, x, y)
print(egcd(a,b))

第三题（Modular Arithmetic 1）

分析下吧，先说下同余
同余“≡”是数论中表示同余的符号

同余的定义如下

给定一个正整数m，如果两个整数a和b满足a-b能被m整除，即(a-b)modm=0，那么就称整数a与b对模m同余，记作a≡b(modm)，同时可成立amodm=b。
再次提醒注意，同余与模运算是不同的，a≡b(modm)仅可推出b=amodm

对于第一个问题，我们需要找到一个整数x，使得11和x在模6下是同余的。因为6是一个较小的数，我们可以手动计算11除以6的余数，然后将余数减去11，直到得到一个小于6的余数。这样的余数就是我们要找的x。

11除以6的商是1，余数是5，因此我们可以将11减去5，得到6，这是6的一个倍数，因此我们可以得出11 ≡ 5 模 6。由于5是小于6的，因此5是我们要找的最小非负整数x。

对于第二个问题，我们需要找到一个整数y，使得8146798528947和y在模17下是同余的。因为这个数太大，我们需要使用计算器来进行计算。

我们可以使用Python中的模运算符号%来计算这个问题。具体来说，我们可以计算8146798528947除以17的余数，这样的余数就是我们要找的y。Python代码如下：

y = 8146798528947 % 17
计算结果是4，因此8146798528947 ≡ 4 模 17。因为4是小于17的，因此4是我们要找的最小非负整数y。
因此，x = 5，y = 4是这两个问题的答案。

第四题（Modular Arithmetic 2）

在学习这道题之前，先了解下费马定理吧，如下：
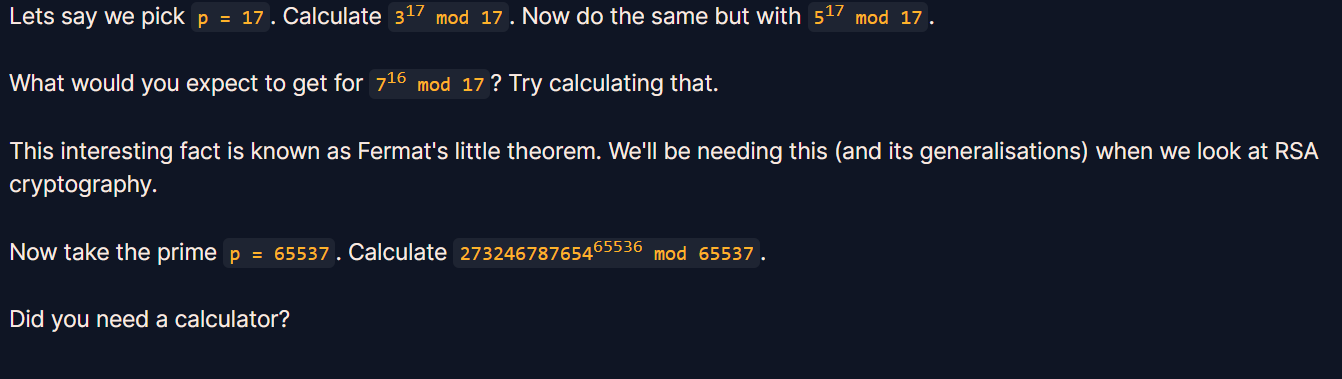
费马定理是数论中的一个基本定理，由法国数学家皮埃尔·德·费马于17世纪提出。该定理的原始形式是：对于任何素数p和任何不是p的倍数的正整数a，a的p-1次方减去1能够被p整除，即a^(p-1) ≡ 1 (mod p)。

换句话说，如果p是一个素数，那么对于任何不是p的倍数的正整数a，a的p-1次方对p取模的结果为1。这个定理的一个重要应用是在密码学中的RSA算法，其中大素数的选取基于费马定理。

费马定理的证明较为复杂，这里不再赘述。值得一提的是，当p是一个合数（即非素数）时，费马定理并不成立，这是因为如果p是一个合数，那么a^(p-1)除以p的余数可能不为1，例如，当a=2，p=15时，2^14 ≡ 1 (mod 15)不成立。

回到这道题，273246787654^65536 mod 65537,根据费马定理a^(p-1) ≡ 1 (mod p)，取p=65537，则在进行模运算273246787654 % 65537 =1，即答案为1.

第五题（Modular Inverting）

在模运算中，如果我们要解决形如a * x ≡ b mod m的方程，其中a，b，m是已知整数，x是未知整数，我们可以使用扩展欧几里得算法来找到x的值。但是，如果m是一个质数，我们可以使用费马小定理来计算a的逆元，即a关于模m的倒数。

具体来说，如果p是一个素数，a是p的倍数之外的任意整数，那么a的逆元a^-1就是满足下列等式的整数b：

a * b ≡ 1 mod p

这里，b就是a在模p意义下的逆元。例如，假设我们要求解3在模13意义下的逆元，也就是找到一个整数b满足3 * b ≡ 1 mod 13。根据费马小定理，3^11 ≡ 1 mod 13，因此3的逆元就是3^10，即9。因为3 * 9 ≡ 1 mod 13。

综上所述，如果我们知道一个数a在模p意义下的逆元b，那么我们就可以用a * b ≡ 1 mod p来验证b是不是a的逆元，也可以用a * b对p取模来计算a在模p意义下的倒数。
python代码如下：

def find_inverse(a, p):
    """
    使用费马小定理计算a在模p意义下的逆元。
    """
    if gcd(a, p) != 1:
        raise ValueError("a和p必须互质")
    return pow(a, p-2, p)

def gcd(a, b):
    """
    使用欧几里得算法计算a和b的最大公因数。
    """
    if b == 0:
        return a
    else:
        return gcd(b, a % b)
print(find_inverse(3,13))

第六题（Quadratic Residues)

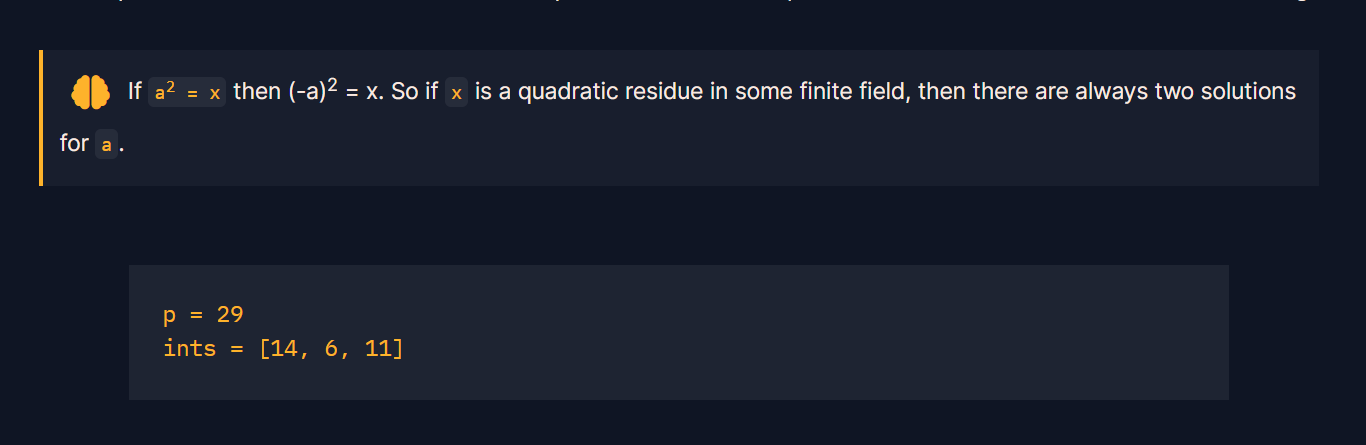
 在模块化算术中，模平方剩余 (QR) 是一个整数，它与完全平方模某个整数模的整数全等。更正式地说，如果存在整数 x，则整数 a 是对整数 p 取模的二次留数，使得：

x^2 ≡ a (mod p)

如果这样的整数 x 存在，我们说 a 是二次留数模 p 并写成 a ≡ x^2 (mod p)。

如果不存在这样的整数 x，则 a 称为二次无余数模 p。

所有二次留数模 p 的集合用 QR(p) 表示，所有二次模非平方剩余 p 的集合用 QNR(p) 表示。

确定一个整数是二次剩余还是非剩余模给定素数 p 是数论中的一个重要问题，在密码学、编码理论和其他领域有各种应用。二次互易定律提供了一个强大的工具来确定二次留数和非留数模素数，以及计算勒让德符号，勒让德符号是一个相关的数学函数，可用于确定二次留数和非留数对任何奇数取模。
题目给了p = 29 , i n ts = [ 14 , 6 , 11 ]，找到三个书中的QR的那一个，解出这个数的模平方根，小的一个根即flag.
上代码：

def quad_residue(x, p):
    """
    检查 x 是否是有限域 F_p 中的二次留数。
如果 x 是二次剩余，则返回 True，否则返回 False。
    """
    for a in range(1, p):
        if pow(a, 2, p) == x:
            return True
    return False

def solve_quad_residue(x, p):
    """
    在有限域 F_p 中求解方程 a^2 = x，其中 p 是质数模数。
返回两个解的元组（如果存在），如果 x 不是二次残差则返回 None。
    """
    if not quad_residue(x, p):
        return None
    solutions = []
    for a in range(1, p):
        if pow(a, 2, p) == x:
            solutions.append(a)
            solutions.append(p - a) # 添加负解
            break
    return tuple(solutions)


p = 29
ints = [14, 6, 11]
for x in ints:
    print(f"x = {x}")
    solutions = solve_quad_residue(x, p)
    if solutions:
        print(f"Solutions: {solutions}")
    else:
        print("Not a quadratic residue")

第七题（Legendre Symbol）

p = 101524035174539890485408575671085261788758965189060164484385690801466167356667036677932998889725476582421738788500738738503134356158197247473850273565349249573867251280253564698939768700489401960767007716413932851838937641880157263936985954881657889497583485535527613578457628399173971810541670838543309159139
ints = [25081841204695904475894082974192007718642931811040324543182130088804239047149283334700530600468528298920930150221871666297194395061462592781551275161695411167049544771049769000895119729307495913024360169904315078028798025169985966732789207320203861858234048872508633514498384390497048416012928086480326832803, 45471765180330439060504647480621449634904192839383897212809808339619841633826534856109999027962620381874878086991125854247108359699799913776917227058286090426484548349388138935504299609200377899052716663351188664096302672712078508601311725863678223874157861163196340391008634419348573975841578359355931590555, 17364140182001694956465593533200623738590196990236340894554145562517924989208719245429557645254953527658049246737589538280332010533027062477684237933221198639948938784244510469138826808187365678322547992099715229218615475923754896960363138890331502811292427146595752813297603265829581292183917027983351121325, 14388109104985808487337749876058284426747816961971581447380608277949200244660381570568531129775053684256071819837294436069133592772543582735985855506250660938574234958754211349215293281645205354069970790155237033436065434572020652955666855773232074749487007626050323967496732359278657193580493324467258802863, 4379499308310772821004090447650785095356643590411706358119239166662089428685562719233435615196994728767593223519226235062647670077854687031681041462632566890129595506430188602238753450337691441293042716909901692570971955078924699306873191983953501093343423248482960643055943413031768521782634679536276233318, 85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771, 50576597458517451578431293746926099486388286246142012476814190030935689430726042810458344828563913001012415702876199708216875020997112089693759638454900092580746638631062117961876611545851157613835724635005253792316142379239047654392970415343694657580353333217547079551304961116837545648785312490665576832987, 96868738830341112368094632337476840272563704408573054404213766500407517251810212494515862176356916912627172280446141202661640191237336568731069327906100896178776245311689857997012187599140875912026589672629935267844696976980890380730867520071059572350667913710344648377601017758188404474812654737363275994871, 4881261656846638800623549662943393234361061827128610120046315649707078244180313661063004390750821317096754282796876479695558644108492317407662131441224257537276274962372021273583478509416358764706098471849536036184924640593888902859441388472856822541452041181244337124767666161645827145408781917658423571721, 18237936726367556664171427575475596460727369368246286138804284742124256700367133250078608537129877968287885457417957868580553371999414227484737603688992620953200143688061024092623556471053006464123205133894607923801371986027458274343737860395496260538663183193877539815179246700525865152165600985105257601565]

考察二次剩余定理
二次剩余定理表述如下：如果p和q是两个不同的奇素数，则二次剩余x mod p可以通过奇偶性以及符号确定它是否是二次剩余mod q，具体来说：

如果p和q都是形如4k+1的素数，或者都是形如4k+3的素数，则x mod p是二次剩余mod q当且仅当q mod p是二次剩余mod p。
如果p是形如4k+1的素数，q是形如4k+3的素数，则x mod p是二次剩余mod q当且仅当q mod p是二次非剩余mod p。
如果p是形如4k+3的素数，q是形如4k+1的素数，则x mod p是二次剩余mod q当且仅当q mod p是二次剩余mod p。
二次剩余
x^2≡n(mod p)
对于这个方程，求出满足的x.

想要更好了解，推荐下：[(https://blog.csdn.net/weixin_44203780/article/details/104634637)]
再看这道题，直接上代码：

p = 101524035174539890485408575671085261788758965189060164484385690801466167356667036677932998889725476582421738788500738738503134356158197247473850273565349249573867251280253564698939768700489401960767007716413932851838937641880157263936985954881657889497583485535527613578457628399173971810541670838543309159139
ints = [25081841204695904475894082974192007718642931811040324543182130088804239047149283334700530600468528298920930150221871666297194395061462592781551275161695411167049544771049769000895119729307495913024360169904315078028798025169985966732789207320203861858234048872508633514498384390497048416012928086480326832803, 45471765180330439060504647480621449634904192839383897212809808339619841633826534856109999027962620381874878086991125854247108359699799913776917227058286090426484548349388138935504299609200377899052716663351188664096302672712078508601311725863678223874157861163196340391008634419348573975841578359355931590555, 17364140182001694956465593533200623738590196990236340894554145562517924989208719245429557645254953527658049246737589538280332010533027062477684237933221198639948938784244510469138826808187365678322547992099715229218615475923754896960363138890331502811292427146595752813297603265829581292183917027983351121325, 14388109104985808487337749876058284426747816961971581447380608277949200244660381570568531129775053684256071819837294436069133592772543582735985855506250660938574234958754211349215293281645205354069970790155237033436065434572020652955666855773232074749487007626050323967496732359278657193580493324467258802863, 4379499308310772821004090447650785095356643590411706358119239166662089428685562719233435615196994728767593223519226235062647670077854687031681041462632566890129595506430188602238753450337691441293042716909901692570971955078924699306873191983953501093343423248482960643055943413031768521782634679536276233318, 85256449776780591202928235662805033201684571648990042997557084658000067050672130152734911919581661523957075992761662315262685030115255938352540032297113615687815976039390537716707854569980516690246592112936796917504034711418465442893323439490171095447109457355598873230115172636184525449905022174536414781771, 50576597458517451578431293746926099486388286246142012476814190030935689430726042810458344828563913001012415702876199708216875020997112089693759638454900092580746638631062117961876611545851157613835724635005253792316142379239047654392970415343694657580353333217547079551304961116837545648785312490665576832987, 96868738830341112368094632337476840272563704408573054404213766500407517251810212494515862176356916912627172280446141202661640191237336568731069327906100896178776245311689857997012187599140875912026589672629935267844696976980890380730867520071059572350667913710344648377601017758188404474812654737363275994871, 4881261656846638800623549662943393234361061827128610120046315649707078244180313661063004390750821317096754282796876479695558644108492317407662131441224257537276274962372021273583478509416358764706098471849536036184924640593888902859441388472856822541452041181244337124767666161645827145408781917658423571721, 18237936726367556664171427575475596460727369368246286138804284742124256700367133250078608537129877968287885457417957868580553371999414227484737603688992620953200143688061024092623556471053006464123205133894607923801371986027458274343737860395496260538663183193877539815179246700525865152165600985105257601565]

solution = []
for a in ints:
    result = pow(a,(p-1)//2,p)
    if result == 1:
        solution.append(ints.index(a))
        print(solution)
        flag = pow(a,(p+1)//4,p)
        print("flag=",flag)

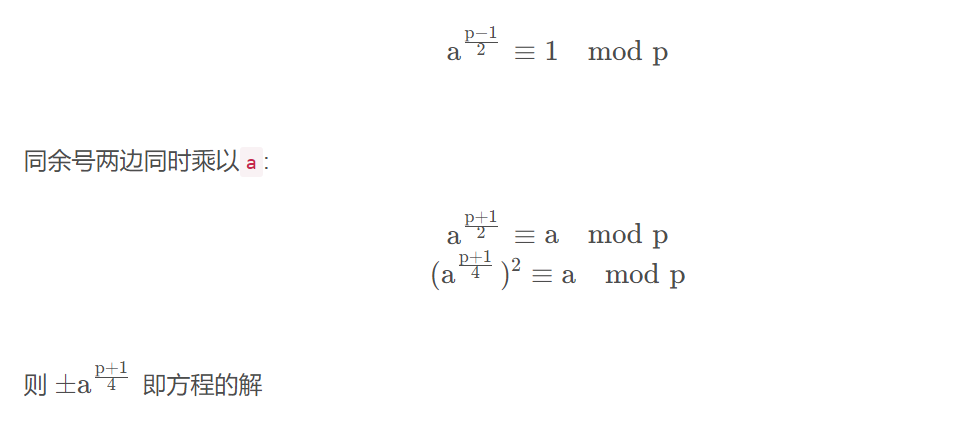
第八题（Modular Square Root）

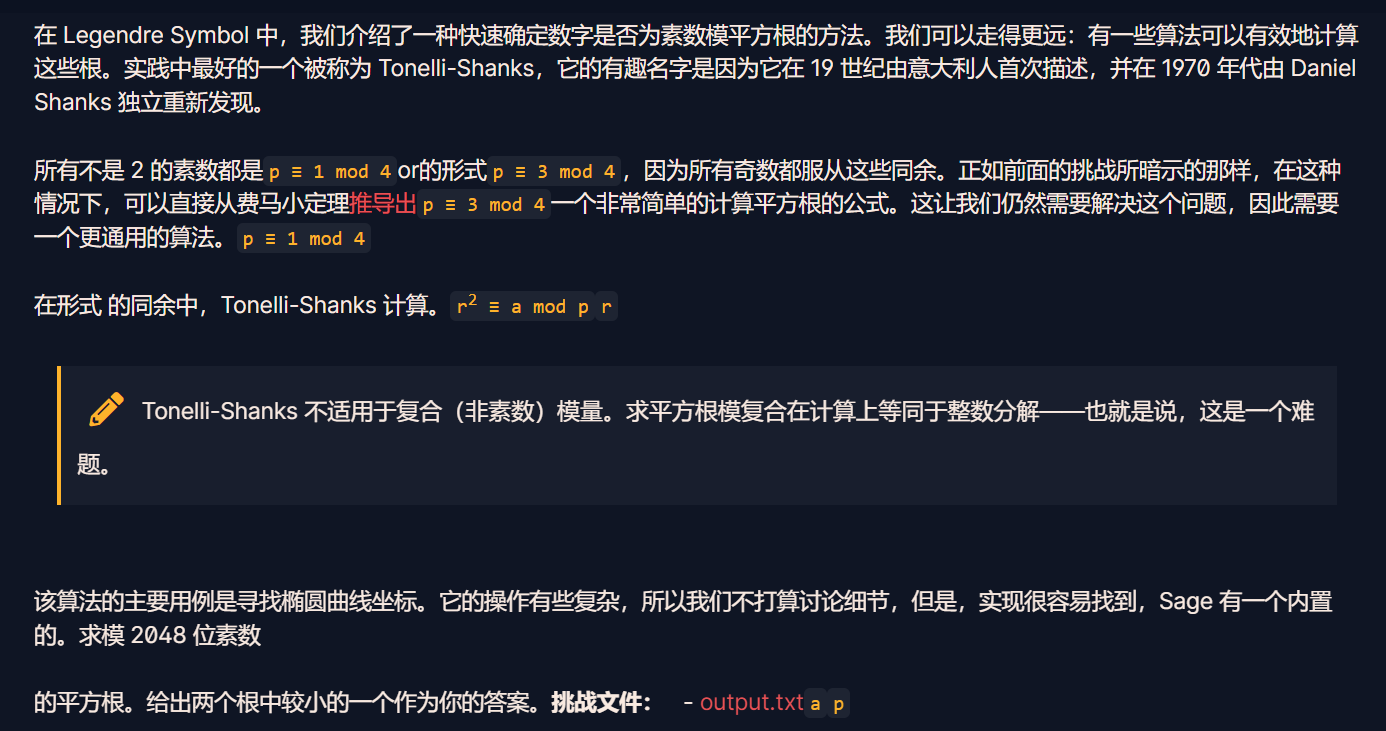
Tonelli-Shanks 算法是一种用于求模质数情况下的平方根的算法。它比一般的试除法和扩展欧几里得算法更高效，特别适合于较大的质数。
该算法要计算椭圆曲线的交点，不深入讨论，但Sage已经有内置的方法实现,python中sympy库也可实现，代码如下：

from sympy import *
a = 8479994658316772151941616510097127087554541274812435112009425778595495359700244470400642403747058566807127814165396640215844192327900454116257979487432016769329970767046735091249898678088061634796559556704959846424131820416048436501387617211770124292793308079214153179977624440438616958575058361193975686620046439877308339989295604537867493683872778843921771307305602776398786978353866231661453376056771972069776398999013769588936194859344941268223184197231368887060609212875507518936172060702209557124430477137421847130682601666968691651447236917018634902407704797328509461854842432015009878011354022108661461024768
p = 30531851861994333252675935111487950694414332763909083514133769861350960895076504687261369815735742549428789138300843082086550059082835141454526618160634109969195486322015775943030060449557090064811940139431735209185996454739163555910726493597222646855506445602953689527405362207926990442391705014604777038685880527537489845359101552442292804398472642356609304810680731556542002301547846635101455995732584071355903010856718680732337369128498655255277003643669031694516851390505923416710601212618443109844041514942401969629158975457079026906304328749039997262960301209158175920051890620947063936347307238412281568760161
print(sqrt_mod(a, p))

sqrt_mod(a, p)用于计算在模意义下 a 的平方根（如果存在的话）。
具体来说，如果存在一个整数 b 满足 b^2 ≡ a (mod p)，则 sqrt_mod(a, p) 返回一个值 b。否则，函数将引发 ValueError 异常，表示在模 p 意义下，a 没有平方根。

第九题（Chinese Remainder Theorem）

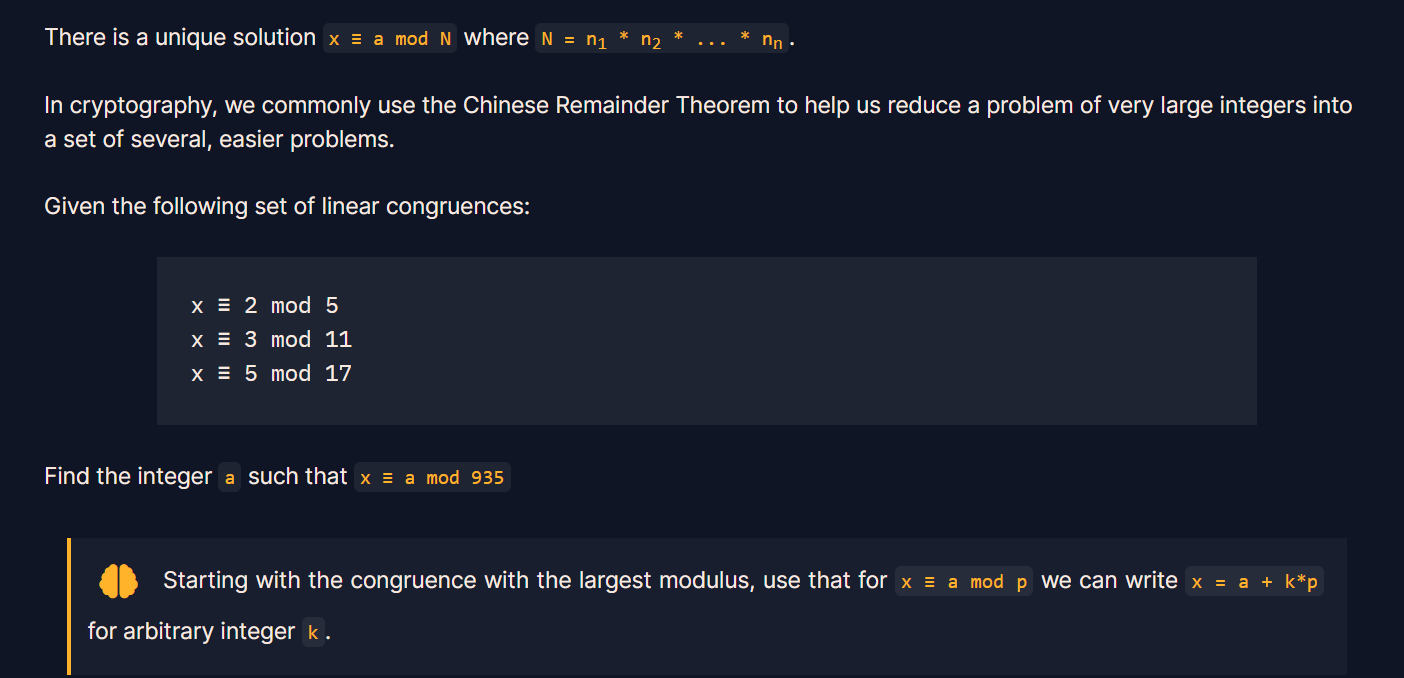
考察中国剩余定理
这个讲的挺详细的[https://www.bilibili.com/video/BV1gf4y1S7LR/]
参考：[(https://www.cnblogs.com/MashiroSky/p/5918158.html)]
我这里就不做过多的赘述了。
然后给出代码：

from functools import reduce
from math import gcd

# 定义同余方程组和模数
eqns = [(2, 5), (3, 11), (5, 17)]
moduli = [5, 11, 17]

# 计算总模数
N = reduce(lambda x, y: x*y, moduli)

# 计算每个模数的逆元
m = [N // m for m in moduli]
mi = [pow(m[i], -1, moduli[i]) for i in range(len(moduli))]

# 计算唯一解
x = sum(a * mi[i] * m[i] for i, (a, _) in enumerate(eqns))

# 输出结果
print("Solution: x = {} (mod {})".format(x % N, N))

第十题（Adrien's Signs）

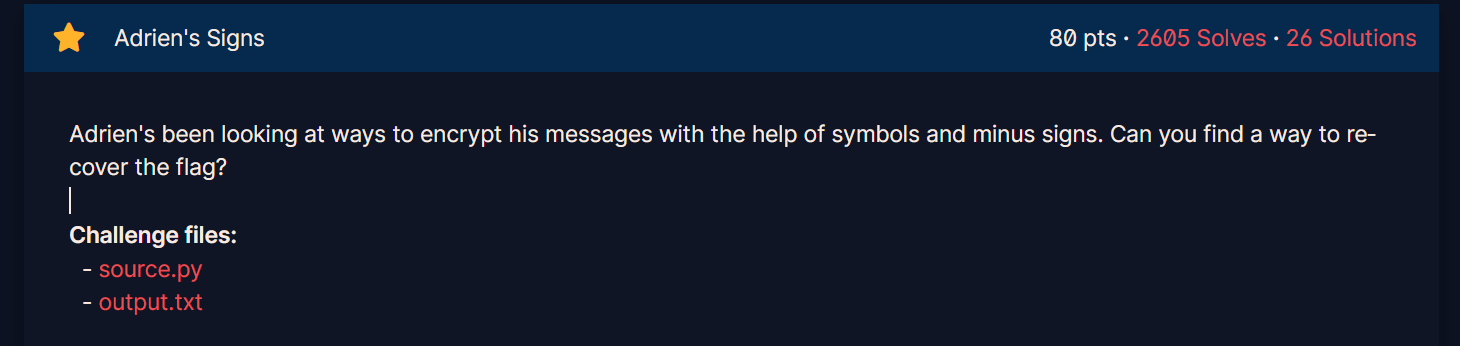
加密代码如图：

上面的代码实现了一个基本的加密方案，用于加密一个二进制格式的标志（flag）。其中，标志的每一位都被独立地加密。加密过程使用了一个基于模幂运算的公钥算法。

公钥由两个参数组成：一个大素数 p 和一个整数 a，其中 a 是模 p 的一个原根。私钥是指数 e，每一位明文都随机选择一个私钥指数。

为了加密单个二进制位，首先将明文位转换为整数 0 或 1。然后，在 1 到 p-1 之间随机选择一个指数 e。对于该位的密文，计算如下：

如果明文为 1，则密文为 a^e mod p
如果明文为 0，则密文为 -a^e mod p
每个位的密文存储在一个列表中，并作为函数的输出返回。

代码中的 FLAG 变量实际上没有被使用，只是一个占位符，用于加密的标志应该作为参数传递给 encrypt_flag 函数。
给出解密代码：

a = 288260533169915
p = 1007621497415251


exec('c=' + open("D:\\temp\\5.txt").read())
from sympy import discrete_log as dl
from tqdm import *  #应用tqdm库显示过程进度
ff = ''
for i in trange(len(c)):
    cc = c[i]
    try:
        r = dl(p,cc,a)
        ff += '1'
    except:
        r = dl(p,-cc%p,a)
        ff += '0'
print(ff)

import libnum
print(libnum.b2s(ff))

第十一题（Modular Binomials）

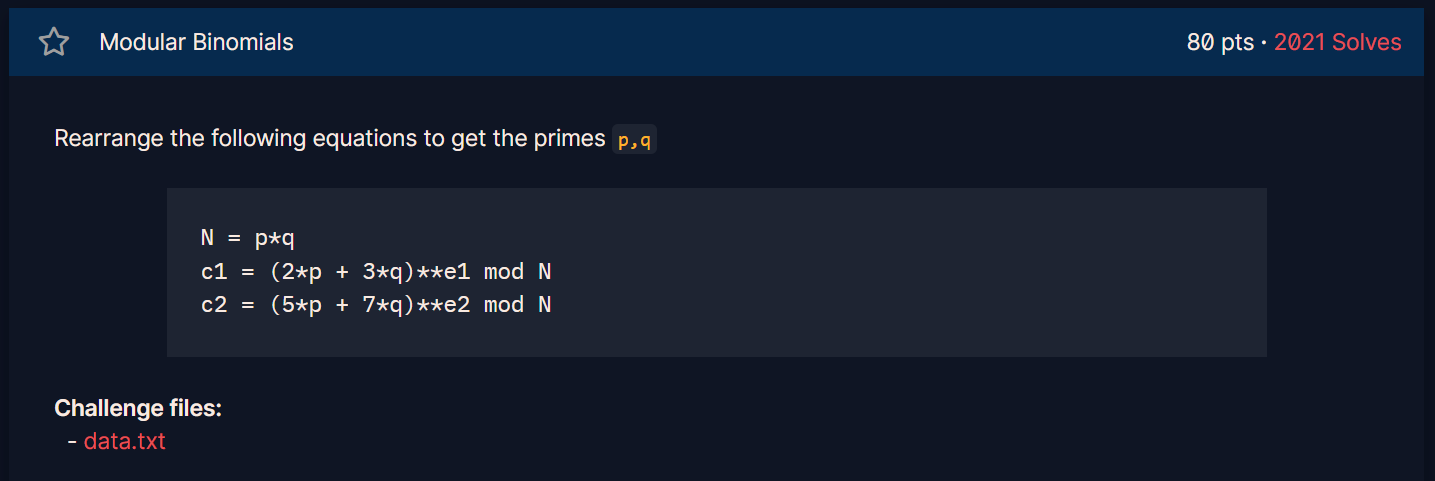
题目说要拿到p,q，第一想法时看一下能不能分解，用factordb试着分解了一下，发现竟然可以

成功拿到p,q。
这道题是一道典型的模二项式的题，可以用模算数定理进行简化
具体实现代码如下：

from math import gcd

n = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519

q1 = pow(c1, e2, n)
q2 = pow(c2, e1, n)

d = pow(5, e1 * e2, n) * q1 - pow(2, e1 * e2, n) * q2

q = gcd(d, n)
p = n // q

assert(p * q == n)
print(p,q)