坐标变换
绕一个轴的旋转
这里写的旋转角与标准的旋转角互为相反数,标准旋转角的定义为面向旋转轴的方向观察,顺时针为正,逆时针为负,ChatGpt给出的结果:[Chat](#Chat)
两个直角坐标系间的变换有6个自由度,分别是\(X 、Y、Z\)的平移和\(\theta_x、\theta_y、\theta_z\)三个绕轴的旋转。
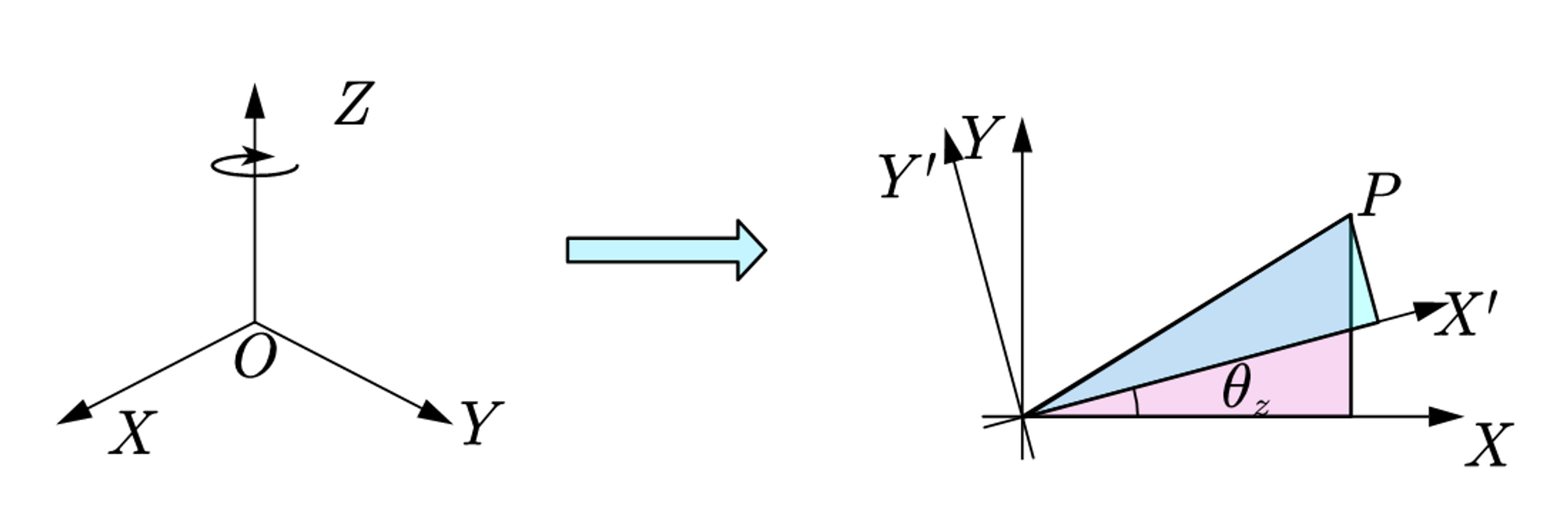
以\(Z\)轴旋转为例,转动一个小角度,得到下列关系式:
\[\begin{array}{}
X'=\frac{X}{\cos{\theta_z}}+(Y-X\tan{\theta_z})\sin(\theta_z)=X\cos{\theta_z}+Y\sin{\theta_z}\\
Y'=(Y-X\tan{\theta_z})\cos(\theta_z)=-X\sin{\theta_z}+Y\cos\theta_z\\
Z'=Z
\end{array}
\]
即:
\[
\left[ \begin{array}{c}
X'\\ Y'\\ Z'\\
\end{array} \right]
=\left[ \begin{matrix}
\cos \theta_
z& \sin \theta_z& 0\\
-\sin \theta_z& \cos \theta_z& 0\\
0& 0& 1\\
\end{matrix} \right]
\left[ \begin{array}{c} X\\ Y\\ Z\\ \end{array} \right] =R_z \left[\begin{array}{c} X\\ Y\\ Z\\ \end{array}\right]
\]
同理:
\[ \ \ R_y=\left[ \begin{matrix} \cos \theta _y& 0& -\sin \theta _y\\ 0& 1& 0\\ \sin \theta _y& 0& \cos \theta _y\\\end{matrix} \right] \ \
R_x=\left[ \begin{matrix} 1& 0& 0\\ 0& \cos \theta _x& \sin \theta _x\\ 0& -\sin \theta _x& \cos \theta _x\\\end{matrix} \right] \]
则坐标变化的公式为:
\[\left[ \begin{array}{c}
X'\\ Y'\\ Z'\\
\end{array} \right]
=R_x R_y R_z
\left[\begin{array}{c}
X\\ Y\\ Z\\
\end{array}\right] +
\left[\begin{array}{c}
x\\ y\\ z\\
\end{array}\right]
\]
任意两个坐标系之间的旋转平移
Drawing 2023-04-14 20.19.22.excalidraw
先考虑两个坐标系之间的旋转关系,再考虑平移就十分简单了。
正交坐标系\(O\)中,三个正交的单位向量:\(e_x,e_y,e_z\)
正交坐标系\(O'\)中,三个正交的单位向量:\(e_{x'},e_{y'},e_{z'}\)
则,一定可以用\(e_x,e_y,e_z\)来表示\(e_{x'},e_{y'},e_{z'}\)。(注意:向量符号的表示与坐标系无关) ,即:
\[\begin{bmatrix}
e_x'\\ e_y' \\e_z'
\end{bmatrix}
=\begin{bmatrix}
a_{11} &a_{12} &a_{13}\\
a_{21} &a_{22} &a_{23}\\
a_{31} &a_{32} &a_{33}
\end{bmatrix}
\begin{bmatrix}
e_x\\ e_y \\e_z
\end{bmatrix}
=R
\begin{bmatrix}
e_x\\ e_y \\e_z
\end{bmatrix}
\]
其中,旋转矩阵中的系数是O'坐标轴向O坐标轴的投影
已知\(P(x,y,z)\),即\(\vec{OP}=xe_x +ye_y+ze_z\),易证:
\[\begin{bmatrix}
x'\\ y' \\z'
\end{bmatrix}
=\begin{bmatrix}
a_{11} &a_{12} &a_{13}\\
a_{21} &a_{22} &a_{23}\\
a_{31} &a_{32} &a_{33}
\end{bmatrix}
\begin{bmatrix}
x\\ y \\ z
\end{bmatrix}
=R
\begin{bmatrix}
x\\ y \\z
\end{bmatrix}
\]
加上平移矩阵:
\[\begin{bmatrix}
x'\\ y' \\z'
\end{bmatrix}
=\begin{bmatrix}
a_{11} &a_{12} &a_{13}\\
a_{21} &a_{22} &a_{23}\\
a_{31} &a_{32} &a_{33}
\end{bmatrix}
\begin{bmatrix}
x\\ y \\ z
\end{bmatrix}
+
\begin{bmatrix}
x_0\\ y_0 \\ z_0
\end{bmatrix}
=R
\begin{bmatrix}
x\\ y \\z
\end{bmatrix}+T
\]
Chat
role::user
如何根据旋转、俯仰和偏航角确定旋转矩阵
role::assistant
旋转、俯仰和偏航角通常用于描述飞行器或机器人在三维空间中的朝向。根据欧拉角的定义,旋转、俯仰和偏航角分别是绕\(Z\)轴、\(Y\)轴和\(X\)轴的旋转角度。因此,可以通过以下步骤确定旋转矩阵:
- 绕\(Z\)轴旋转\(\theta\)角度,得到旋转矩阵\(R_z\):
\[R_z = \begin{bmatrix}
\cos\theta & -\sin\theta & 0 \\
\sin\theta & \cos\theta & 0 \\
0 & 0 & 1
\end{bmatrix}
\]
- 绕\(Y\)轴旋转\(\phi\)角度,得到旋转矩阵\(R_y\):
\[R_y = \begin{bmatrix}
\cos\phi & 0 & \sin\phi \\
0 & 1 & 0 \\
-\sin\phi & 0 & \cos\phi
\end{bmatrix}
\]
- 绕\(X\)轴旋转\(\psi\)角度,得到旋转矩阵\(R_x\):
\[R_x = \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos\psi & -\sin\psi \\
0 & \sin\psi & \cos\psi
\end{bmatrix}
\]
- 将三个旋转矩阵按照\(Z-Y-X\)的顺序相乘,得到最终的旋转矩阵\(R\):
\[R = R_x R_y R_z = \begin{bmatrix}
\cos\theta\cos\phi & \cos\theta\sin\phi\sin\psi - \sin\theta\cos\psi & \cos\theta\sin\phi\cos\psi + \sin\theta\sin\psi \\
\sin\theta\cos\phi & \sin\theta\sin\phi\sin\psi + \cos \theta\cos\psi & \sin\theta\sin\phi\cos\psi - \cos\theta\sin\psi \\
-\sin\phi & \cos\phi\sin\psi & \cos\phi\cos\psi
\end{bmatrix}
\]
这个旋转矩阵\(R\)描述了从一个坐标系到另一个坐标系的旋转变换。例如,如果一个向量\(v\)在原始坐标系中的坐标是\((x,y,z)\),那么在新的坐标系中的坐标\(v'\)可以通过以下公式计算:
\[v' = Rv
\]
其中,\(v\)和\(v'\)都是列向量。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号