第一次作业：深度学习基础

第一次作业：深度学习基础

本周学习内容

动手学深度学习-Pytorch版 1 - 9节课程

本周主要内容是一些简单的基础的深度学习内容的介绍，包括环境的配置，数据的读入和预处理以及基础的数学内容，顺便复习了线性回归的代码实现以及一些损失函数的数学形式化的内容。

---

安装实验所需的d2l库

!pip install d2l

与深度学习相关的数据操作

1.张量基本操作

torch.arange(n)函数作用是生成一个长度为0~n-1组成的张量
torch.zeros(),torch.ones()生成一个指定大小的全0或全1的张量。
也可以通过torch.tensor()函数生成一个指定数值的张量
```python`
import torch
x=torch.arange(12)
print(x)
print(x.shape)
x=x.reshape(3,4)
print(x)
torch.zeros(3,4)
torch.ones(2,3,4)
torch.tensor([[1,3],[2,3]])

输出：

tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
torch.Size([12])
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
tensor([[1, 3],
[2, 3]])

### 2.张量运算
张量可以像数值一样进行基本运算
'+'为将两个张量对应位相加,'/'为张量对应位相除,'**'为张量的乘方
同时可以利用广播机制，来简化一些操作
```python
x=torch.tensor([1.0,2,4,8])
y=torch.tensor([2,3,2,2])
print(x+y)
print(x/y)
print(x**y)

输出：

tensor([ 3.,  5.,  6., 10.])
tensor([0.5000, 0.6667, 2.0000, 4.0000])
tensor([ 1.,  8., 16., 64.])

通过cat函数将两个张量进行连接
reshape()函数可以改变一个张量的形状而不改变元素数量和元素值

x=torch.arange(12,dtype=torch.float32).reshape((3,4))
y=torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
torch.cat((x,y),dim=0)

通过双等号'=='来判断两个张量的元素是否相等

x==y

输出：

tensor([[False,  True, False,  True],
        [False, False, False, False],
        [False, False, False, False]])

通过sum函数对张量的元素求和

x.sum()

输出：

tensor(66.)

3.张量的广播机制

当张量的形状不同时，仍然可以通过调用'广播机制'来执行按元素操作
所谓广播机制，就是将张量填充为相同大小

a=torch.arange(3).reshape((3,1))
b=torch.arange(2).reshape((1,2))
print(a)
print(b)
a+b

输出：

tensor([[0],
        [1],
        [2]])
tensor([[0, 1]])
tensor([[0, 1],
        [1, 2],
        [2, 3]])

4. 张量的读取与写入

可以用 [-1] 选择最后一个元素，可以用 [1:3] 选择第二个和第三个元素来进行读取
除读取外，我们还可以通过指定索引来将元素写入矩阵，具体示例如代码第四行所示
为多个元素赋值相同的值，只需要索引所有元素，然后为它们赋值，具体示例如第六行所示

print(x[-1])
print(x[1:3])
print(x)
x[1,2]=9
print(x)
x[0:2,:]=12
x

矩阵点积,点积是相同位置的按元素乘积的和
可以通过.dot()函数求矩阵点积，也可以通过执行按元素乘法，然后进行求和来表示两个向量的点积

y = torch.ones(4, dtype=torch.float32)
x, y, torch.dot(x, y)
torch.sum(x * y)

输出：

tensor([0., 1., 2., 3.])
tensor(6.)
tensor(6.)

矩阵向量积\(Ax\)是一个长度为m的列向量，其第i个元素是点积\(a_i^Tx\)

A=torch.arange(20).reshape(5,4)
print(A.shape)
print(A)
x=torch.tensor([0,1,2,3])
torch.mv(A,x)#矩阵向量积

输出：

torch.Size([5, 4])
tensor([[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11],
        [12, 13, 14, 15],
        [16, 17, 18, 19]])
tensor([ 14,  38,  62,  86, 110])

可以将矩阵-矩阵乘法AB看作是简单地执行m次矩阵-向量积，并将结果拼接在一起，形成一个n×m矩阵

B=torch.ones((4,3),dtype=torch.int64)
torch.mm(A,B)

输出：

tensor([[ 6,  6,  6],
        [22, 22, 22],
        [38, 38, 38],
        [54, 54, 54],
        [70, 70, 70]])

求矩阵范数
L₂范数是向量元素平方和的平方根

\[||x||_2=\sqrt{\sum_{i=1}^nx_i^2} \]

L₁范数是所有元素绝对值的和

\[||x||_1={\sum_{i=1}^n|x_i|} \]

矩阵的弗罗贝尼乌斯范数（Frobenius norm）是矩阵元素平方和的平方根

\[||x||_F=\sqrt{\sum_{i=1}^m\sum_{j=1}^nx_{ij}^2} \]

u=torch.tensor([3.0,4.0])
print(torch.norm(u))#L2范数  
torch.abs(u).sum()#L1范数
torch.norm(torch.ones((4, 9)))#F范数

输出：

tensor(5.)
tensor(7.)
tensor(6.)

自动求导

1.标量的反向传播

2.非标量变量的反向传播

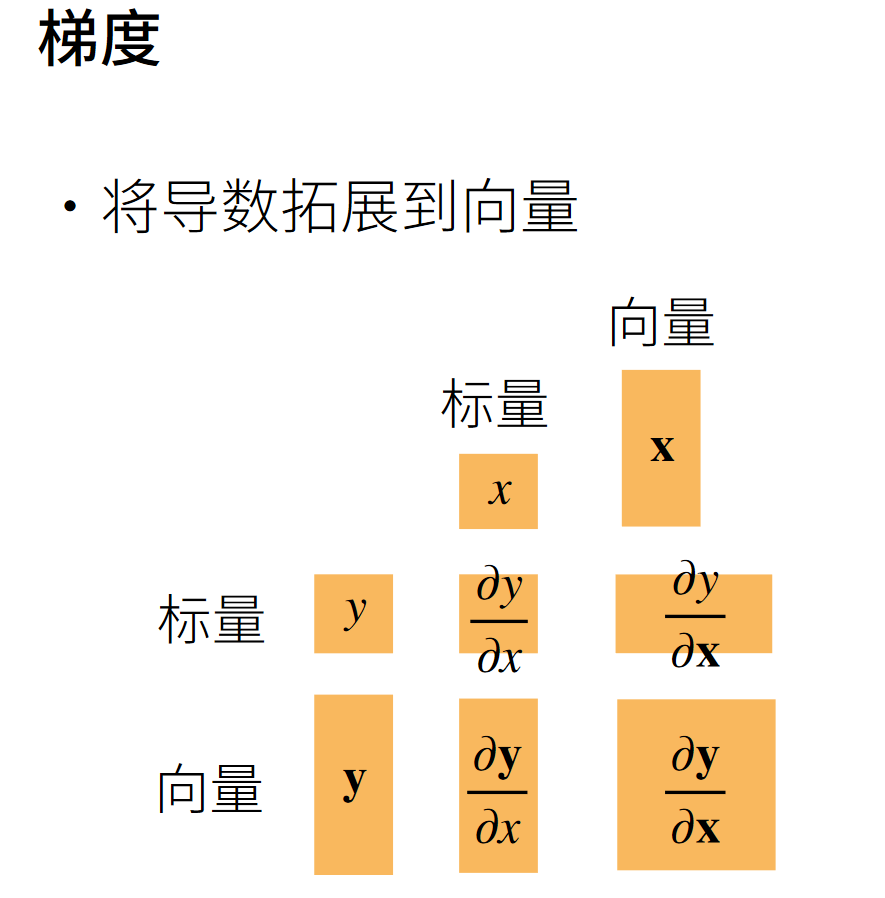
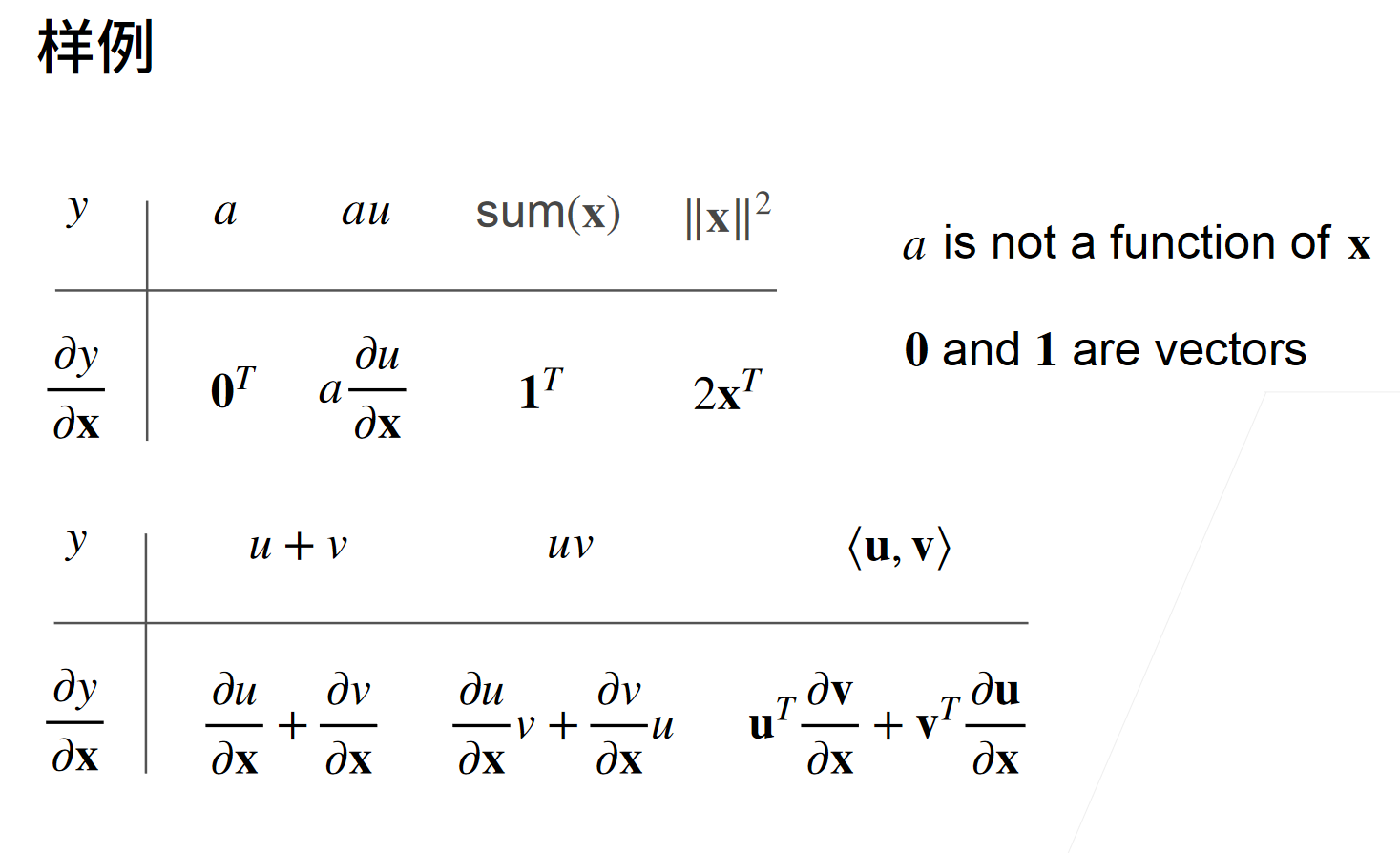
当y不是标量时，向量y关于向量x的导数的最自然解释是一个矩阵。对于高阶和高维的y和x，求导的结果可以是一个高阶张量。

存在的问题

1. 对线性代数已经概率上的东西比较久没有接触，不是特别的理解
2. 对python代码比较手生，记不住用法了

收获

复习了一些线性代数有关的知识还有深度学习的基础的内容，包括数据处理等
还有就是，最快的学习方式就是从代码开始