Leetcode 第 210 场周赛

记录最长的没匹配右括号的左括号

class Solution {
public:
    int maxDepth(string s) {
        int d = 0;
        int ans=0;
        for (char c : s){
            if (c == '(') {
                ++d;
                ans = max(ans, d);
            }
            else if(c==')'){
                --d;
            }
        }
        return ans;
    }
};

暴力n方的求即可，因为点个数很少
否则可能需要对边枚举

class Solution {
public:
    int G[100][100];
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        memset(G, 0, sizeof G);
        vector<int> in(n,0);
        for(auto e:roads){
            G[e[0]][e[1]]=1;
            G[e[1]][e[0]]=1;
            in[e[0]] ++;
            in[e[1]]++;
        }
        int ans = 0;
        for(int i=0; i<n; i++){
            for(int j=i+1; j<n; j++){
                if(G[i][j]){
                    ans = max(ans, in[i]+in[j]-1);
                
                }
                else ans = max(ans, in[i]+in[j]);
            }
        }
        return ans;
    }
};

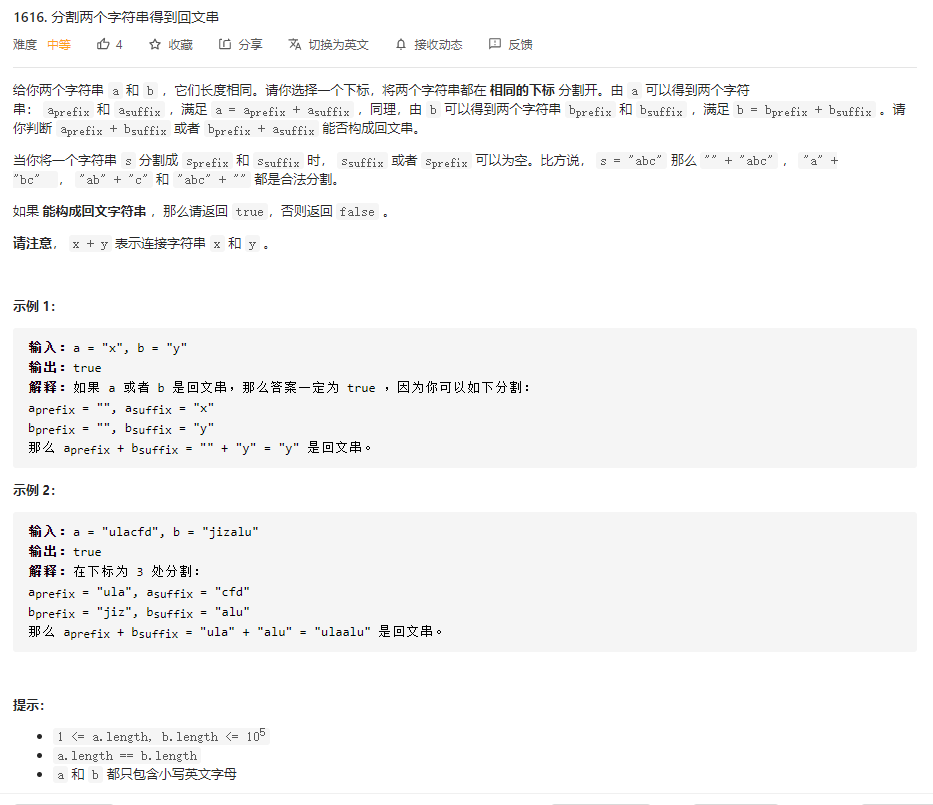
可以发现 如果a[0:i] 与 b[n-i-1:n-1]相匹配
而且可以构成回文，那么必然有a[i+1:n-i-2]是回文
或者b[i+1:n-i-2]是回文
所以分别把a和b当第一个串走一遍双指针就可以
复杂度O(n)

class Solution {
public:
    bool checkPalindromeFormation(string a, string b) {
        string c = a;
        string d = b;
        int n = a.size();
        reverse(a.begin(), a.end());
        reverse(b.begin(), b.end());
        if(a==c||b==d) return true;
        int i=0;
        int j=n-1;
        while(i<j&&c[i]==d[j]) i++, j--;
        int a1=i;
        int a2=j;
        while(i<j&&c[i]==c[j]) i++,j--;
        while(a1<a2&&d[a1]==d[a2])  a1++, a2--;
        if(i>=j||a1>=a2) return true;
        i=0, j=n-1;
        while(i<j&&d[i]==c[j])  i++, j--;
         a1=i;
            a2=j;
        while(i<j&&c[i]==c[j]) i++,j--;
        while(a1<a2&&d[a1]==d[a2]) a1++, a2--;
         if(i>=j||a1>=a2) return true;
        return false;
        
    }
};

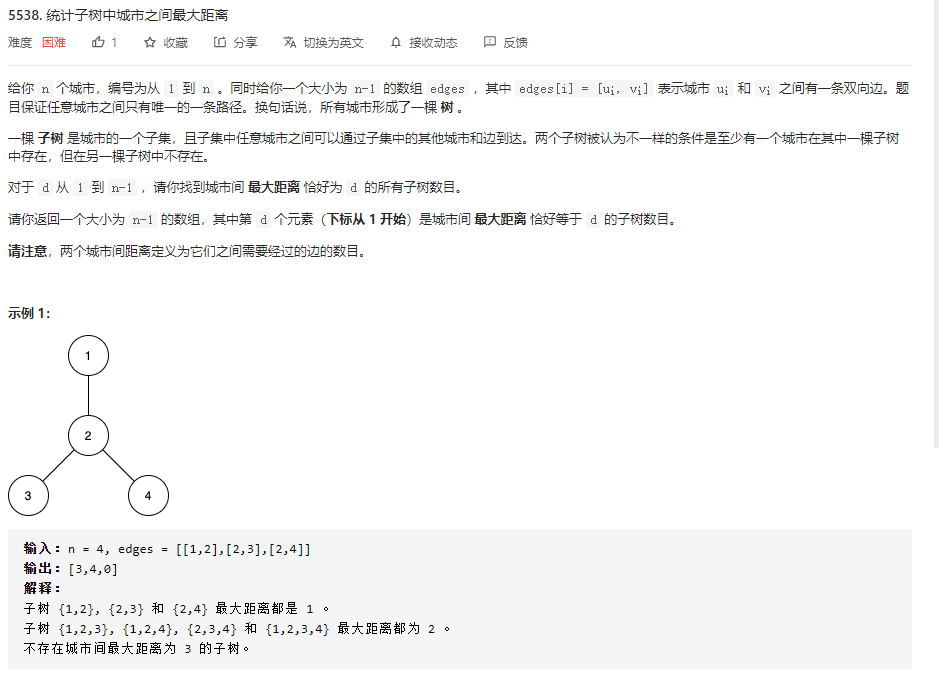
因为n的值非常小，只有15
不难想到枚举所有子集的复杂度只有O(2^n）
然后对每个子集构成的子树求最大距离也就是
求直径，可以用树形dp复杂度O(n)
总复杂度O(n2^n)

leetcode卡我vector离谱

#define ll long long 
class Solution {
public:
    int ans = 0;
    int d[16];
    vector<vector<int>> G;
    void dp(int beg, vector<int>& in, int fa){
        int ma = 0;
        if(G[beg].size()==0)
            d[beg]=0;
        for(auto e:G[beg]){
            if(e==fa||!in[e])
                continue;
            dp(e, in, beg);
            ans = max(ans, d[beg]+d[e]+1);
            d[beg] = max(d[beg], d[e]+1);
        }
        
    }
    vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {
        vector<int> res(n-1,0);
        G = vector<vector<int>>(16, vector<int>());
        for(auto e:edges){
                G[e[0]].push_back(e[1]);
                G[e[1]].push_back(e[0]);
            }
            
        for(int i=1; i<(1<<n); i++){
            int c = __builtin_popcount(i);
            if(c<=1)
                continue;
            vector<int> in(16, 0);
            for(int j=0; j<=n; j++){
                if(i&(1<<j)){
                    in[j+1] = 1;
                }
            }
            int cnt = 0;
            int beg;
           for(auto e:edges){
                if(in[e[0]]&&in[e[1]]){
                    cnt ++;
                    beg=e[0];
                }
            }
            
            if(cnt!=c-1)
                continue;
            ans = 0;
            memset(d,0,sizeof d);
            dp(beg, in, -1);
            res[ans-1]++;
        }
        return res;
    }
};