Leetcode BiWeekly Contest 31
- 在区间范围内统计奇数数目
给你两个非负整数 low 和 high 。请你返回 low 和 high 之间(包括二者)奇数的数目。
示例 1:
输入:low = 3, high = 7
输出:3
解释:3 到 7 之间奇数数字为 [3,5,7] 。
示例 2:
输入:low = 8, high = 10
输出:1
解释:8 到 10 之间奇数数字为 [9] 。
提示:
0 <= low <= high <= 10^9
小学数学
class Solution {
public:
int countOdds(int low, int high) {
int ans = (high-low+1+1)>>1;
if((low&1)||(high&1))
return ans;
return ans-1;
}
};
- 和为奇数的子数组数目
给你一个整数数组 arr 。请你返回和为 奇数 的子数组数目。
由于答案可能会很大,请你将结果对 10^9 + 7 取余后返回。
示例 1:
输入:arr = [1,3,5]
输出:4
解释:所有的子数组为 [[1],[1,3],[1,3,5],[3],[3,5],[5]] 。
所有子数组的和为 [1,4,9,3,8,5].
奇数和包括 [1,9,3,5] ,所以答案为 4 。
示例 2 :
输入:arr = [2,4,6]
输出:0
解释:所有子数组为 [[2],[2,4],[2,4,6],[4],[4,6],[6]] 。
所有子数组和为 [2,6,12,4,10,6] 。
所有子数组和都是偶数,所以答案为 0 。
示例 3:
输入:arr = [1,2,3,4,5,6,7]
输出:16
示例 4:
输入:arr = [100,100,99,99]
输出:4
示例 5:
输入:arr = [7]
输出:1
老套路了,记录前缀和奇数和偶数的个数
计算包含当前元素时的答案个数
int mod = 1e9+7;
class Solution {
public:
int numOfSubarrays(vector<int>& arr) {
//prefixsum and cal the number of odd and even number before it
for(int i=1; i<arr.size(); i++)
arr[i] += arr[i-1];
int ans = 0;
int a[]={0,0};
for(int i=0; i<arr.size(); i++){
a[arr[i]&1]++;
if(arr[i]&1){
ans = (ans+a[0]+1)%mod;
}else
ans = (ans+a[1])%mod;
}
return ans;
}
};
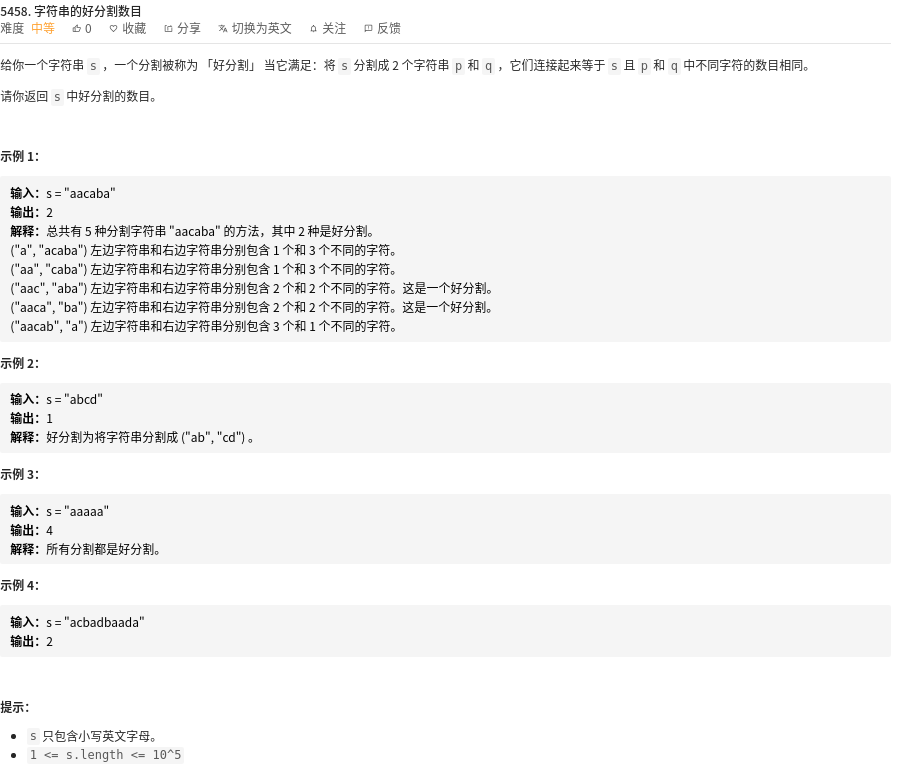
前缀一次求不同的字母个数
从后面循环求解
class Solution {
public:
int numSplits(string s) {
vector<int> cnt(s.length());
int occur[26];
memset(occur, 0, sizeof occur);
int num=0;
for(int i=0; i<s.length(); i++){
if(!occur[s[i]-'a']){
occur[s[i]-'a']=1;
num++;
}
cnt[i]=num;
}
num=0;
int ans=0;
memset(occur, 0, sizeof occur);
for(int i=s.length()-1; i>0; i--){
if(!occur[s[i]-'a']){
occur[s[i]-'a']=1;
num++;
}
if(num==cnt[i-1]) ans++;
if(num>cnt[i-1]) break;
}
return ans;
}
};
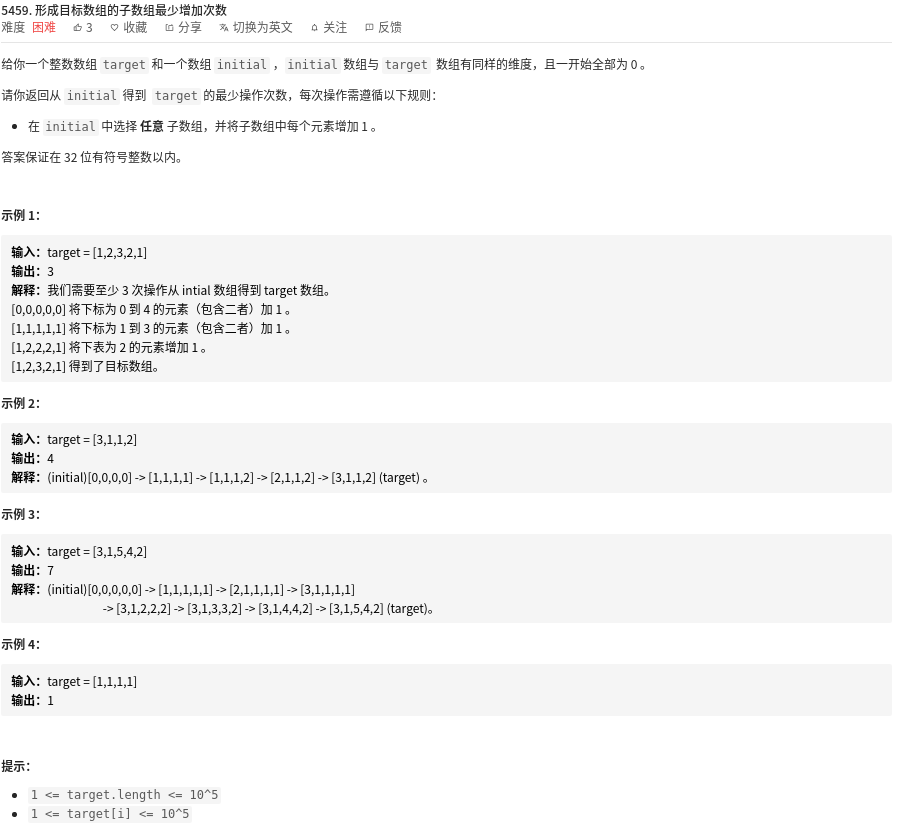
直觉告诉我们,如果当前元素比后一个元素小
那么: 对当前元素进行增加的同时而不对后一个增加的话结果肯定不是最优的
而如果当前元素比后一个元素大,那么肯定前面大的那个尖的塔要被消去
所以只需要顺序扫描一次,每当后一个比当前小,就累加差距,为了方便在数组后面加一个0
class Solution {
public:
int minNumberOperations(vector<int>& target) {
target.push_back(0);
int ans=0;
for(int i=0; i<target.size()-1; i++){
if(target[i]>target[i+1]){
ans+=target[i]-target[i+1];
}
}
return ans;
}
};
一条有梦想的咸鱼

