leetcode 第 29 场双周赛

直接暴力做法，排序之后去掉最大最小就行
线性做法应该就直接记录最大最小，但是没必要

---

class Solution {
public:
    double average(vector<int>& a) {
        sort(a.begin(), a.end());
        double ans = 0;
        for(auto e:a)
            ans += e;
        ans -= a[0];
        ans -= a.back();
        return ans/(a.size()-2);
    }
};

手速场就是舒服，直接O(sqrt(N))求因子，然后排序一下输出

class Solution {
public:
    int kthFactor(int n, int k) {
        vector<int> ans;
        for(int i=1; i*i<=n; i++){
            if(n%i==0){
               ans.push_back(i);
            if(i*i!=n)
                ans.push_back(n/i);
                    
            }
        }
        sort(ans.begin(), ans.end());
        return ans.size()<k?-1:ans[k-1];
    }
};

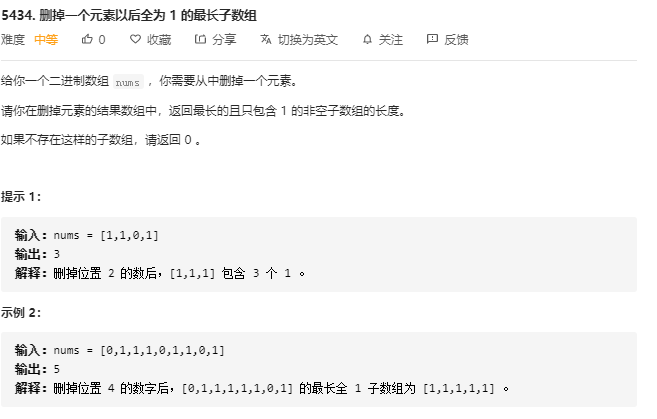
记录前缀和后缀的1的个数，貌似写复杂了
双指针应该可以更快而且节省空间

class Solution {
public:
    int longestSubarray(vector<int>& a) {
        vector<int> b(a.size()+5, 0), c(a.size()+5, 0);
        for(int i=0; i<a.size(); i++){
            if(a[i]==1)
                b[i+1]=b[i]+1;
            else{
               b[i+1]=0;
            }
        }
         for(int i=a.size()-1; i>=0; i--){
            if(a[i]==1)
                c[i]=c[i+1]+1;
            else{
               c[i]=0;
            }
        }
        int ans=0;
        for(int i=0; i<a.size(); i++){
            ans = max(ans, b[i]+c[i+1]);
        }
        return ans;
    }
};

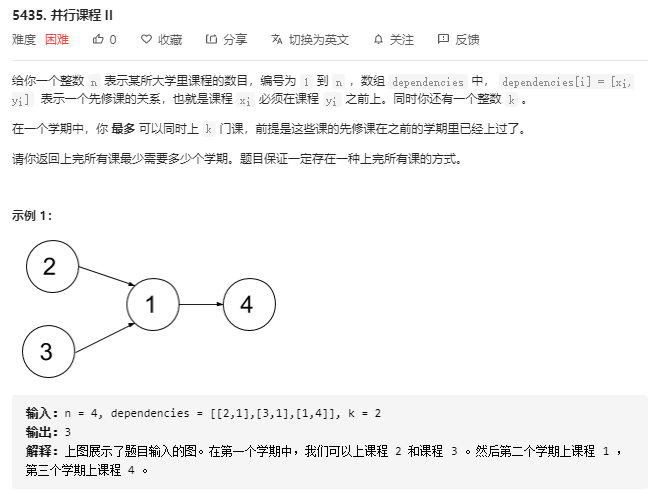
这道题，虽然过了但是很羞愧，用的是个假算法

---

假算法
1. 求每个节点的出度的大小
2. 对图利用优先队列进行一波拓扑排序
但是这个贪心策略是有问题的，在面对出度相同的时候
而且节点可选个数多于k时，会出现错误

---

struct Node{
    int no;
    int child;
    Node(){
        no=0;
        child=0;
    }
    friend bool operator<(const Node& a,const  Node& b){
        return a.child<b.child;
    }
};

class Solution {
public:
    int minNumberOfSemesters(int n, vector<vector<int>>& dep, int k) {
        priority_queue<Node> pq;
        Node no[16];
        vector<int> in(n+1, 0);
        for(int i=0; i<16; i++)
            no[i].no=i;
        vector<vector<int>> G(n+1, vector<int>(0));
        for(auto e:dep){
            in[e[1]]++;
            no[e[0]].child += 1;
            G[e[0]].push_back(e[1]);
        }
        int ans = 0;
        for(int i=1; i<=n; i++){
            if(in[i]==0)
                pq.push(no[i]);
        }
        vector<int> temp;
        cout<<pq.size()<<endl;
        while(!pq.empty()){
            cout<<ans<<endl;
            ans++;
            temp.clear();
            int cnt=0;
            while(!pq.empty()&&cnt<k){
                cnt++;
                Node te = pq.top();
                pq.pop();
                for(auto i:G[te.no]){
                    in[i]--;
                    if(in[i]==0)
                        temp.push_back(i);
                }
            }
            for(auto i:temp)
                pq.push(no[i]);
        }
        return ans;
    }
};

---

正确的做法：
状压dp, 课程用一个整数的二进制位表示
则dp[i|chose] = min(dp[i|chose], dp[i]+1)
其中i表示当前已经修过的课
chose表示下一个学期可以修的课

---

class Solution {
    public final int INT_MAX = 101;
    public int[] dp =null;  //dp数组
    public int minNumberOfSemesters(int n, int[][] dependencies, int k) {
        dp = new int[1<<n];
        for(int i=0; i<1<<n; i++)
            dp[i] = INT_MAX;
        dp[0]=0;
        for(int[] e:dependencies){
            e[0] -= 1;
            e[1] -= 1;
        }
        
        for(int i=0; i<1<<n; i++){
            int unable=0;
            for(int[] e:dependencies){
                if((i>>e[0]&1)==0)
                    unable |= 1<<e[1];
            }
            int can = 0;
            for(int j=0; j<n; j++){
                if((unable>>j&1)==0&&(i>>j&1)==0)
                    can |= 1<<j;
            }
            dfs(n, k, i, can, 0, 0);
        }
        return dp[(1<<n)-1];
    }
    public void dfs(int n, int k, int i, int can, int chosed, int start){
        if(k==0||can==0){
            dp[i|chosed] = Math.min(dp[i|chosed], dp[i]+1);
            return;
        }
        for(int j=start; j<n; j++){
            if((i>>j&1)==0 && (can>>j&1)==1)
                dfs(n, k-1, i, can-(1<<j), chosed+(1<<j), j+1);
        }
    }
}