2.1 刚体运动的向量矩阵描述
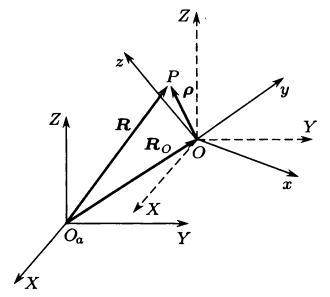
\[\boldsymbol{R}=\boldsymbol{R_O}+\boldsymbol{A\rho}
\]
- \(O_aXYZ\) 固定坐标系。
- O是刚体上任意固定点,称为基点。\(OXYZ\) 是平动坐标系,从固定坐标系通过平动位移获得。
- \(Oxyz\) 是固连坐标系,它与刚体固结在一起。研究刚体的运动主要是研究固连坐标系的运动。
- P 是刚体上某点,\(\boldsymbol{\rho}=\overrightarrow{OP}\) 是该点在固连坐标系 \(Oxyz\) 中的分量,显然它不随时间变化。\(\overrightarrow{OP}\) 在 \(OXYZ\) 中的分量用 \(\boldsymbol{r}\) 表示:
\[\boldsymbol{r}=\boldsymbol{A\rho}
\]
- 在刚体运动过程中,上式中 \(\boldsymbol{R}_O\) 和 \(A\) 是时间的函数。
刚体的定点运动
- 定点运动:运动过程中,刚体上存在点 O 始终保持不动。可见此时 \(\boldsymbol{R}_O\) 为常量。
变换矩阵 A 的特殊性
设 \(Oxyz\) 坐标系三个坐标轴的单位向量为 \(i',j',k'\) 。那么:
\[\begin{aligned}
r&=\rho_xi'+\rho_yj'+\rho_zi'\\
&=\left[i',j',k'\right]
\begin{bmatrix}
\rho_x\\
\rho_y\\
\rho_z\\
\end{bmatrix}
\end{aligned}
\]
所以:
\[A=\left[i',j',k'\right]
\]
由于 \(i',j',k'\) 两两正交,所以 \(\boldsymbol{A}\boldsymbol{A}^T=\boldsymbol{E}\) , \(\boldsymbol{A}\) 为正交矩阵。
还有由 \(\boldsymbol{A}\boldsymbol{A}^T=E\) 可得 \((\text{det}\boldsymbol{A})^2=1\)。所以 \(\text{det}\boldsymbol{A}=\pm1\) ,初始没有运动的情况下 \(Oxyz\) 与 \(OXYZ\) 重合, \(\text{det}A=1\),由于矩阵 \(\boldsymbol{A}\) 对时间 t 的连续性,可知 \(\text{det}\boldsymbol{A}=1\) 恒成立
刚体有限位移基本定理
欧拉定理 刚体定点运动的任意位移都可以通过绕过该定点的某个轴的一次转动实现。
证明 先证明变换矩阵 A 必有特征值 1
\[\begin{aligned}
矩阵\boldsymbol{A}的特征多项式:\qquad&
f(\lambda)=\text{det}(\boldsymbol{A}-\lambda\boldsymbol{E})
\\
\\
求f(1):\qquad&
\begin{aligned}
f(1)&=\text{det}(\boldsymbol{A}-\boldsymbol{E})\\
&=\text{det}(\boldsymbol{A}^T-\boldsymbol{E}^T)\\
&=\text{det}(\boldsymbol{A}^{-1}-\boldsymbol{E})\\
&=\text{det}(\boldsymbol{A}^{-1}(\boldsymbol{E}-\boldsymbol{A}))\\
&=\text{det}(\boldsymbol{A}^{-1})\text{det}(\boldsymbol{E}-\boldsymbol{A})\\
&=\text{det}(\boldsymbol{E}-\boldsymbol{A})\\
&=(-1)^3\text{det}(\boldsymbol{A}-\boldsymbol{E})\\
&=-f(1)\\
\Rightarrow&f(1) = 0
\end{aligned}
\end{aligned}
\]
变换矩阵 A 必有特征值 1,因此特征值 1 对应的特征向量 \(\boldsymbol{r}\) 满足:
\[\boldsymbol{A}\boldsymbol{r}=\boldsymbol{r}
\]
对于任意定点运动的位移,都存在某一特点方向,平行于该方向的向量大小方向都不发送变化。特征向量的方向即为转轴的方向,定点运动可看做绕过定点的平行于该特征向量的轴的旋转运动。
由矩阵 A 求绕轴的转角
建立固接在刚体上的另一个坐标系 \(OX'Y'Z'\) ,使 \(Z'\) 轴平行于转轴,设转角为 \(\alpha\) ,绕 \(Z'\) 轴旋转 \(\alpha\) ,对应的变换矩阵:
\[\boldsymbol{A}'=
\begin{bmatrix}
\cos\alpha& -\sin\alpha& 0\\
\sin\alpha& \cos\alpha& 0\\
0& 0& 1
\end{bmatrix}
\]
\(\boldsymbol{A}\) 和 \(\boldsymbol{A}'\) 相似,相似矩阵的迹相等,有:
\[1+2\cos\alpha=a_{11}+a_{22}+a_{33}
\]
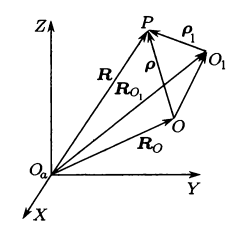
夏莱定理 刚体最一般的位移可以分解为随任选基点的平动位移和绕通过基点的某个轴的转动。选择刚体上不同的点为基点,这种分解方法不唯一;选择不同的基点时平动位移的长度和方向将改变,而转动轴的方向和转角不依赖于基点的旋转。
\[\begin{aligned} \boldsymbol{R} & =\boldsymbol{R}_O+\boldsymbol{A} \boldsymbol{\rho}=\boldsymbol{R}_O+\boldsymbol{A}\left(\overline{O O}_1+\boldsymbol{\rho}_1\right) \\ & =\boldsymbol{R}_O+\boldsymbol{A} \overline{O O}_1+\boldsymbol{A} \boldsymbol{\rho}_1=\boldsymbol{R}_{O_1}+\boldsymbol{A}\boldsymbol{\rho}_1\end{aligned}
\]
莫茨定理 刚体最一般的位移是螺旋位移