Matlab实现相机标定
MatLab工具箱实现相机标定
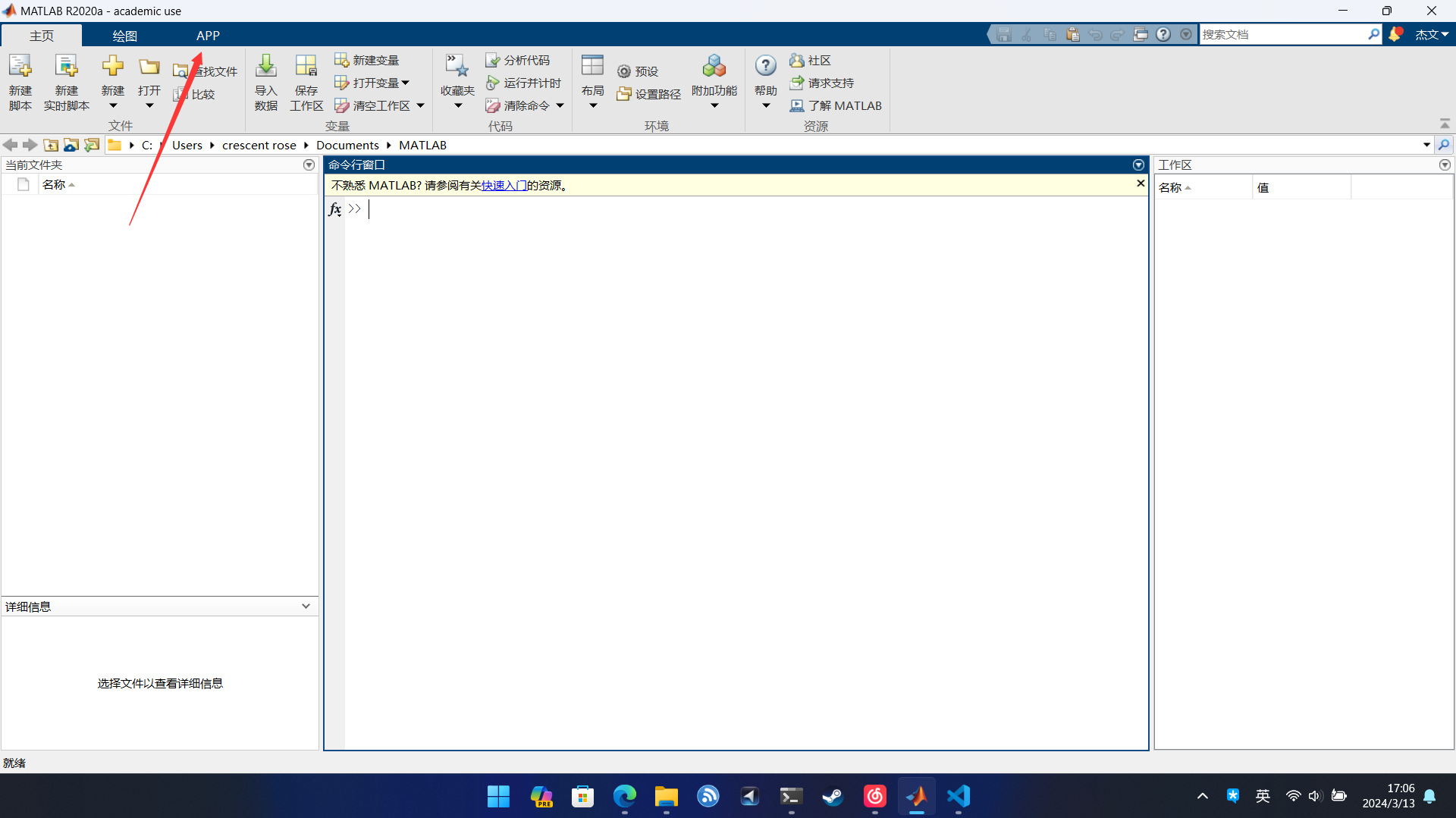
- 打开Matlab找到App界面
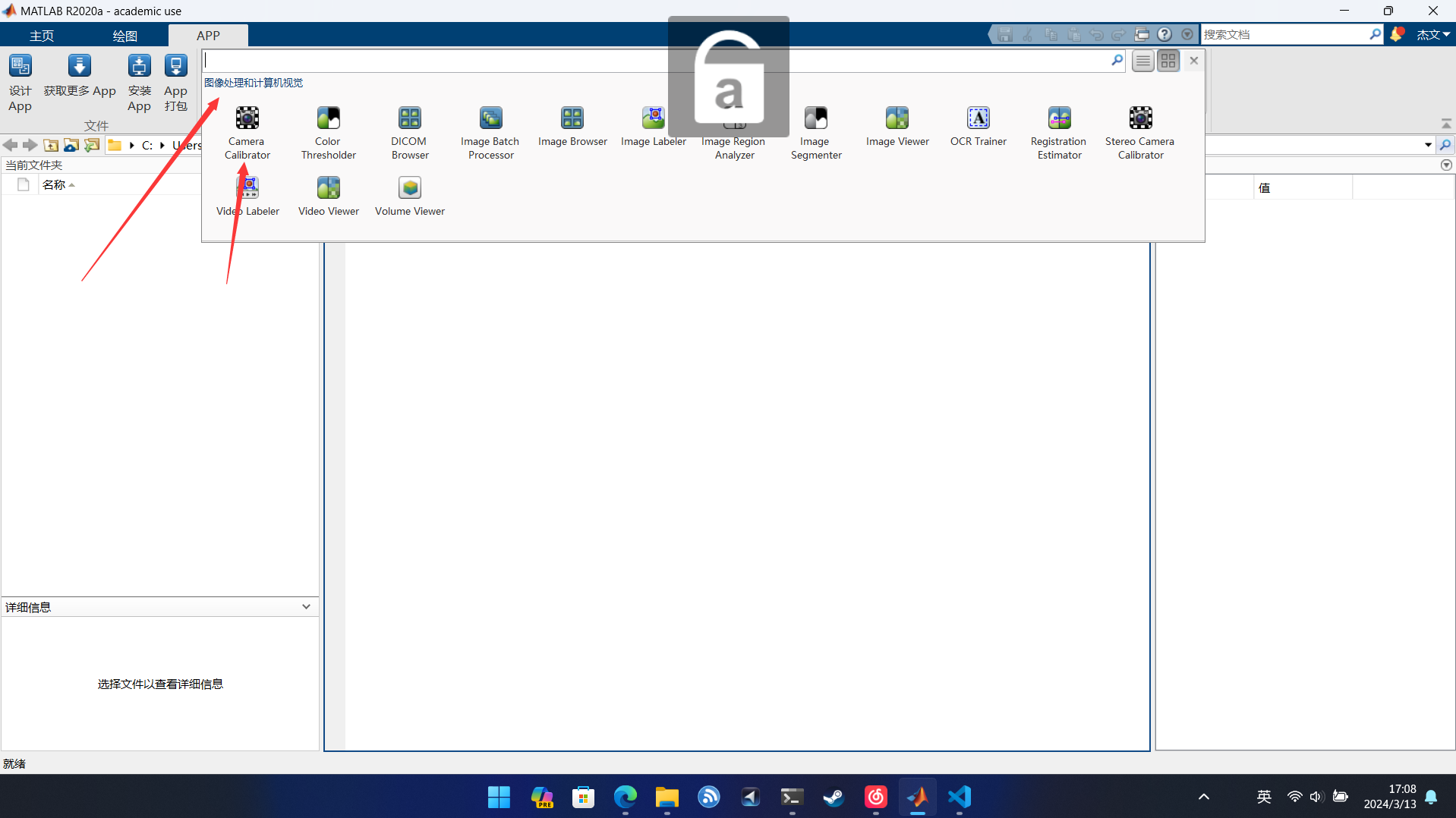
- 找到图像处理与计算机视觉工具箱(Computer Vision ToolBox),找到CameraCalibrator(相机标定)工具，一般就是第一个。打开CameraCalibrator工具。
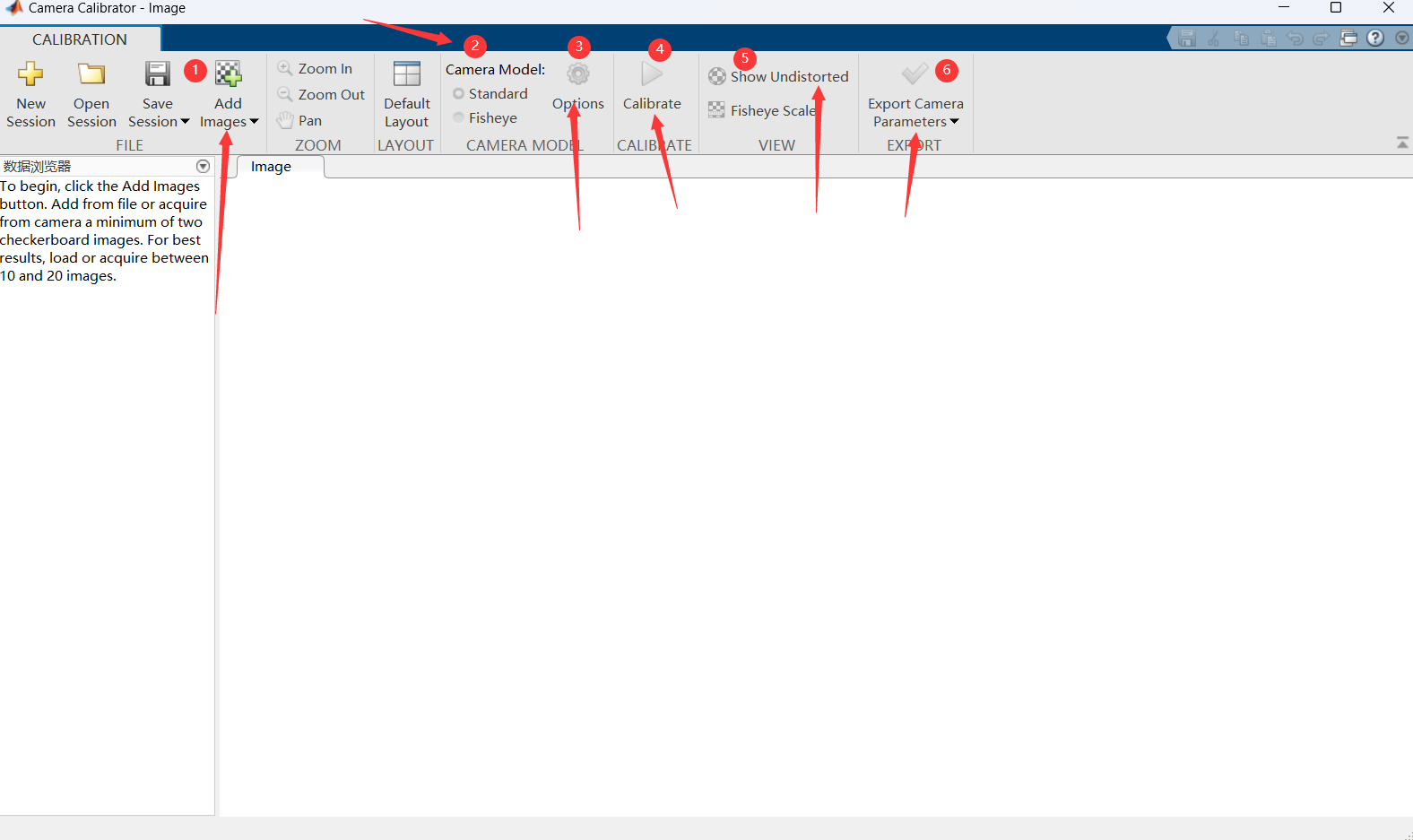
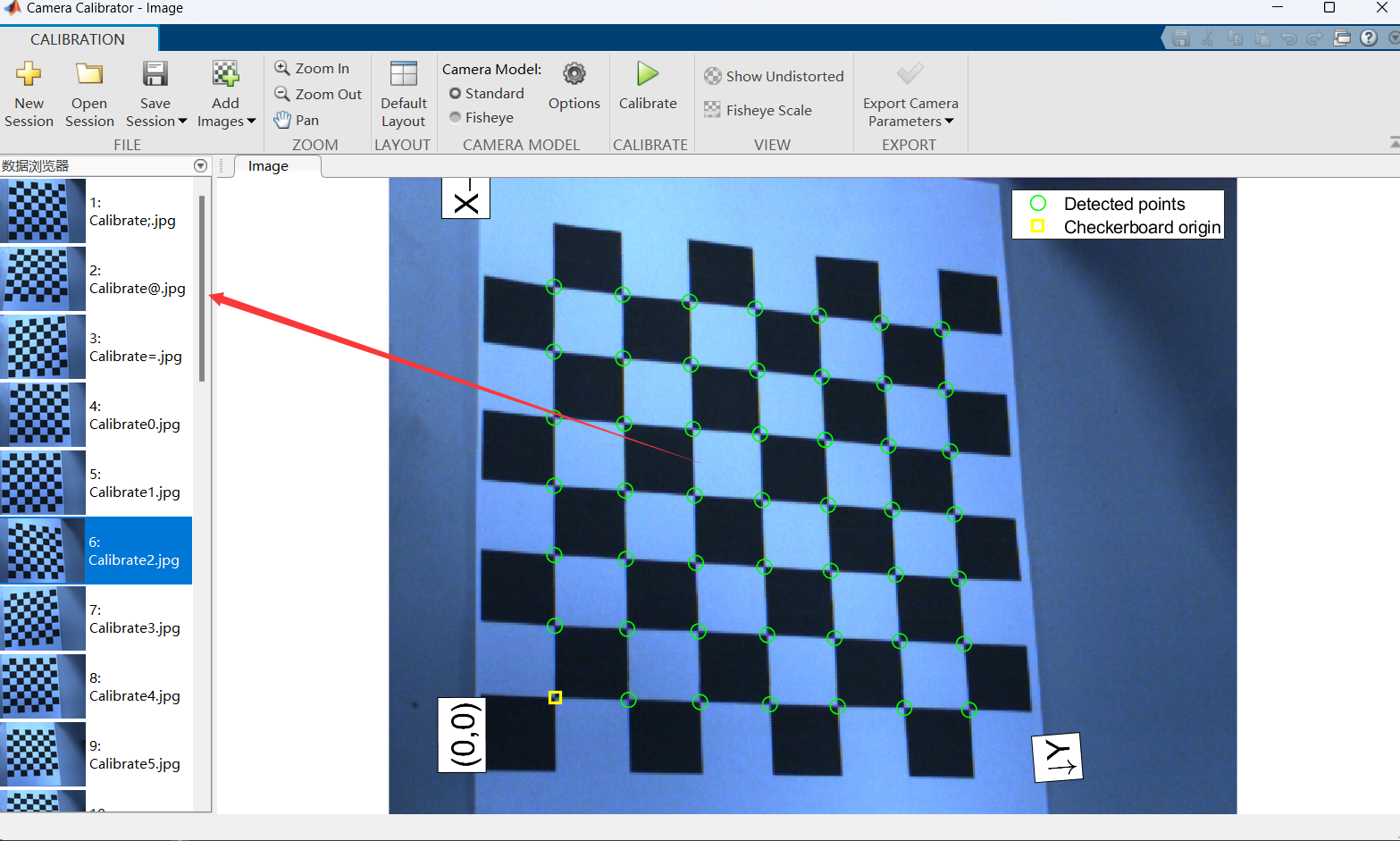
- 下图就是打开后的界面。
其中有几个功能
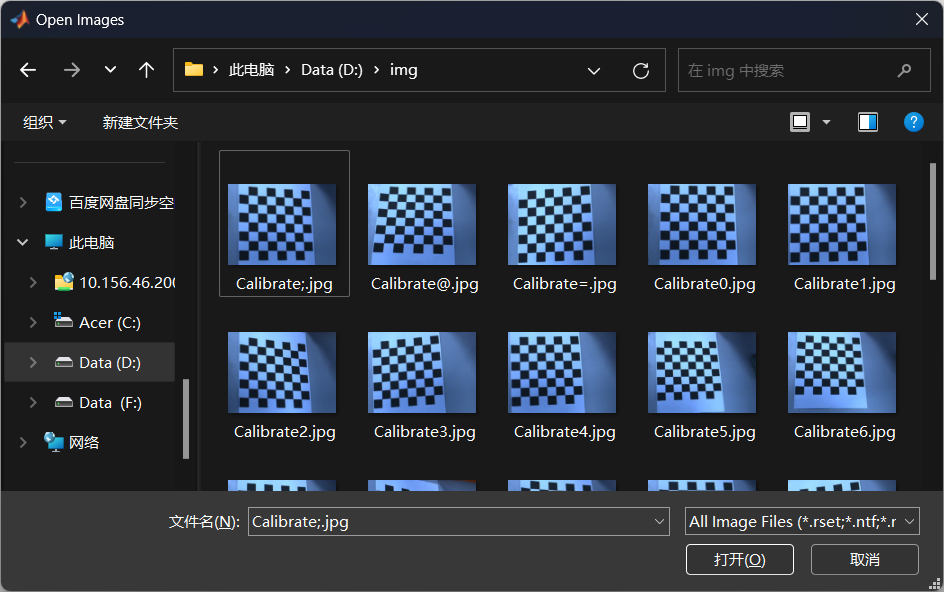
- Add Images，添加用于标定的图像，如棋盘格。打开后让你选择需要标定的图像，只能以单张图象为单位加入，不支持文件夹类型。可以按住Ctrl选择需要的图片，也可以使用Ctrl+A来全部选择。选择完毕后点击打开即可。
打开后会出现
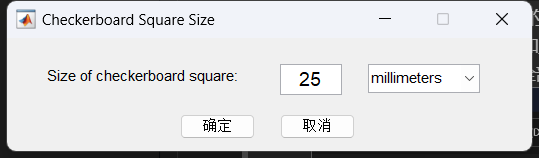
填入拍摄的棋盘格一个格子的边长，右边可以选择单位(mm,cm,英寸)。填完后点击确定。
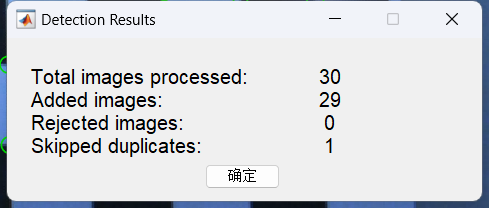
然后Matlab会自动找出棋盘格的内角点，结束后出现如下提示框：
第一行是一共处理了多少图像，第二行是接受了也就是成功处理了多少图像，第三行是拒绝了也就是拍摄模糊或者拍摄错误导致棋盘格内角点无法识别的图像，这样的图像不会用于标定，第四行是重复了多少图像。
左边栏会出现找完角点后的棋盘格，标注了棋盘格内角点的世界坐标系的起点以及坐标轴。
值得注意的是，拍摄的棋盘格的纵横格子数如果都一样(也就是看起来像正方形)，Matlab会爆出一个警告
警告: The checkerboard must be asymmetric: one side should be even, and the other should be odd. Otherwise, the
orientation of the board may be detected incorrectly.
因为通常根据棋盘格长宽格子数的不同来分辨一组图片中各个棋盘格的世界坐标系并正确的标出，若长宽一样可能会导致世界坐标标注错误。因此最好选用长宽不一样的棋盘格。
- Camera Model,选择相机模型，可以选择标准模型(针孔模型)(Standard)或者鱼眼相机模型(fisheye)。一般选择标准模型即可。
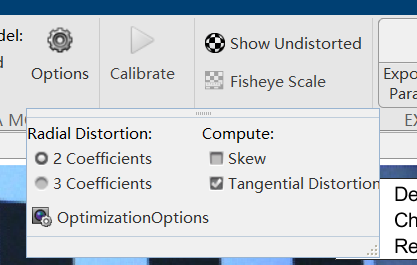
- Options，标定时的一些设置。
第一列选择的是选择标定时想要获取的径向畸变(Radial-径向，Distortion-畸变)的参数个数，第一个是两个参数，即只有径向畸变的\([k_1\quad k_2]\)这两个参数。第二个选择是三个参数，即变成了\([k_1\quad k_2 \quad k_3]\)这三个参数。一般勾选上三个参数径向畸变参数计算。
第二列选择的是否计算切向畸变，一般会勾选上第二个选项，即选择计算切向畸变参数\([p_1\quad p_2]\)
- Calibrate三角形按钮，当设置好前面的一些参数时，点击该按钮进行标定。
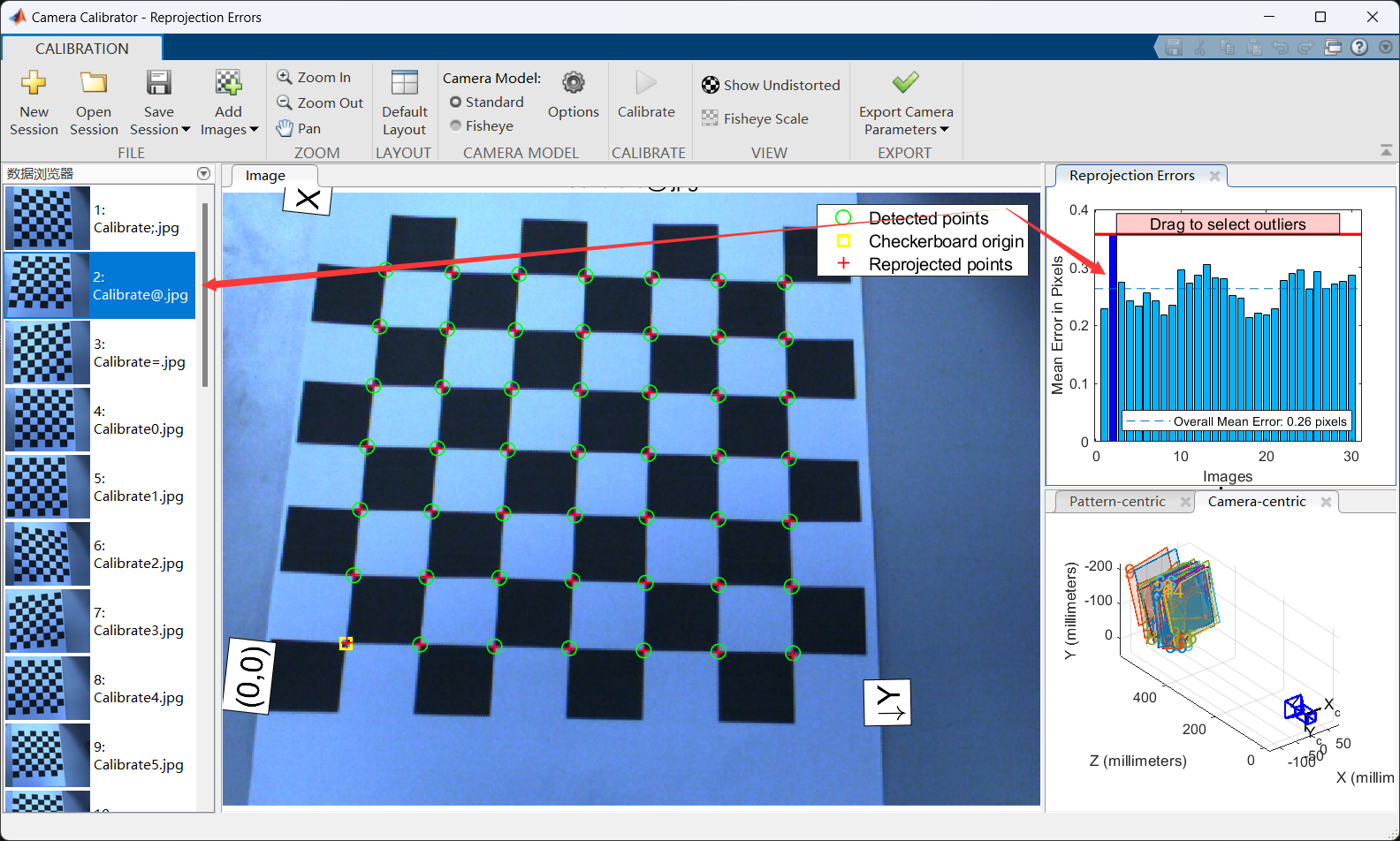
标定结束后，右侧会出现每张图像的重投影误差，重投影误差越大，标定效果越差。当重投影误差小于3pixels时，认为标定效果较好。因此我们可以点击重投影误差较大的柱状图，工具会自动找出对应左边的哪张图片，我们将该张误差较大的图片删除，然后点击Calibrate三角形重新标定即可。
!
- Show Undistorted 展示未畸变的图像，即经过畸变修正过后的图像。当棋盘格为球形时显示原本图像，为方形时显示去畸变后的图像。
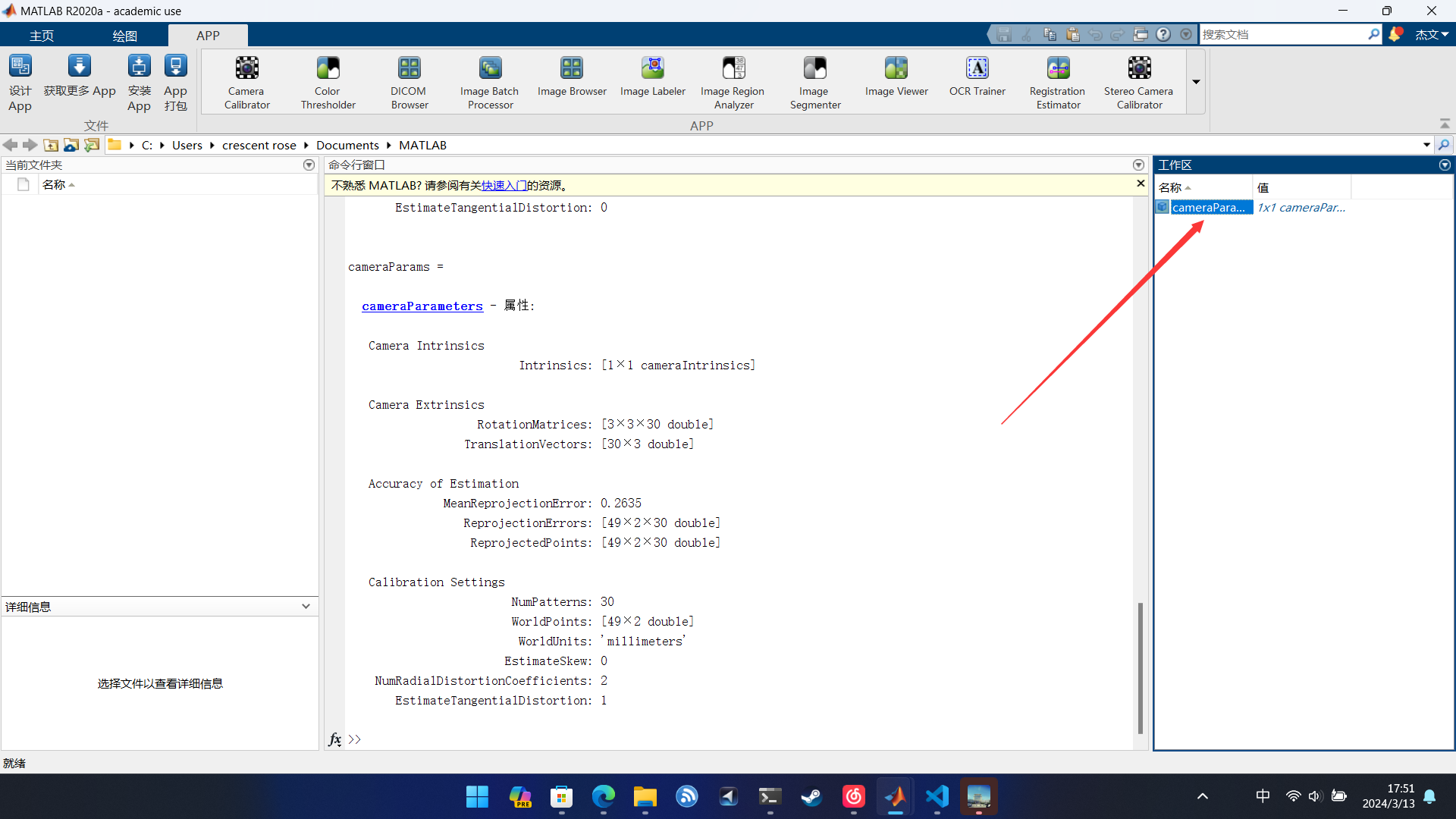
- Export Camera Parameters，导出标定得到的相机参数到Matlab工作区。点击后回到工作区可以看到导出的参数。
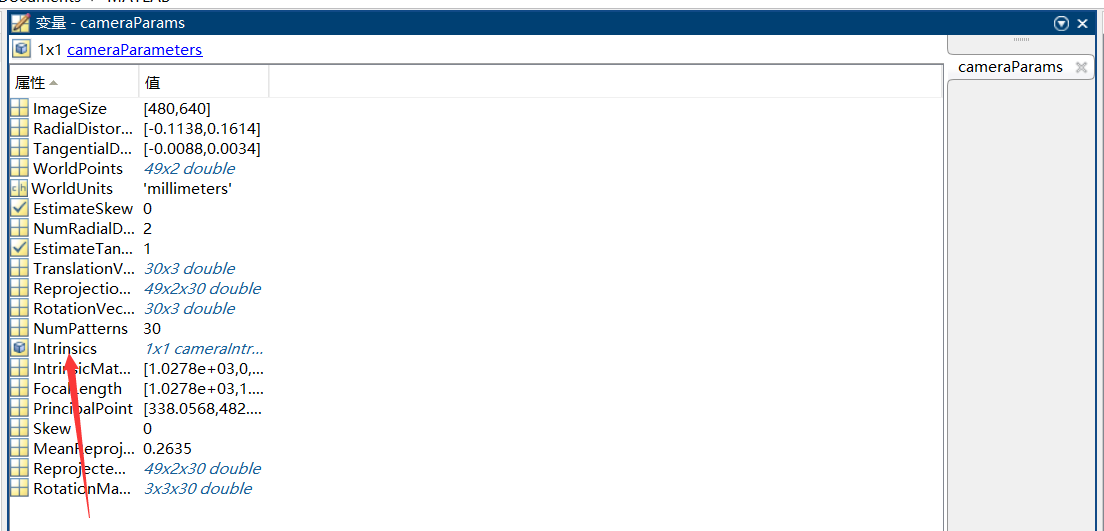
点击后进入详细页面,里面有很多参数，大家可以各取所需，比较关系的时箭头所指的参数，即相机模型的内部参数，包含内参矩阵以及畸变参数。
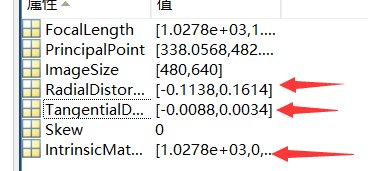
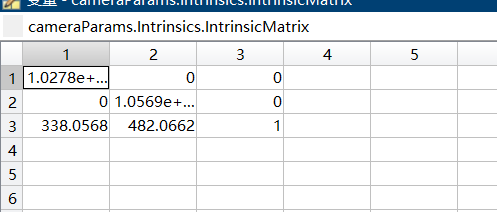
点进去后也会有一些参数。其中比较重要的是RadialDistortion以及TangentialDistortion即径向畸变以及切向畸变的参数\([k_1\quad k_2\quad k_3\quad p_1\quad p_2]\),以及IntrinsicMatrix即内参矩阵。点进去会有其详细的表格参数。
不难看出，Matlab给出的内参矩阵并非标准形式
而是标准形式的转置。
使用时务必注意这一点。且内参矩阵参数的单位都为像素。
最后在提一点，再用OpenCV的
calibrateCamera()函数进行标定时，传出的内参矩阵与标准形式一致，但是畸变矩阵参数向量的排布为下
distCoeffs = [k1 k2 p1 p2 k3]
并非k1 k2 k3 p1 p2,这一点使用时也请注意。
