视觉slam十四讲CH4 ---李群与李代数求导

视觉slam十四讲 ---CH4 李群与李代数求导

李群与李代数相较于CH3是比较的抽象的数学知识，这个工具的提出目的是解决一些旋转位姿描述的优化问题。本讲最终的目的是解决如何描述对旋转求导的问题。

1. 什么是群

群是一种集合加上一种运算的代数结构

记集合为A，运算为\(\cdot\quad\)，则若此结构满足以下几条性质，构成一个群。

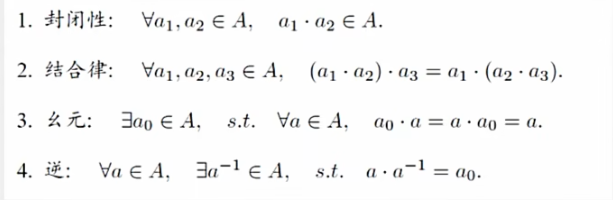
第三讲中的旋转矩阵R以及变换矩阵T加上乘法运算就构成一种群。

特殊正交群

\[SO(3) = \{R\in R^{n\times n}|RR^T = I, det(R) = 1\}\\ \]

特殊欧式群

\[SE(3) = \{ T = \begin{bmatrix} R & t \\ 0^T & 1\\ \end{bmatrix} \in R^{4\times 4} | R \in SO(3),t\in R^3 \} \]

对于SO(3)以及SE(3),它们对于乘法是封闭的，也就是说对于多个旋转矩阵或者变换矩阵相乘，结果仍为旋转矩阵或者变换矩阵。这一点在上一章描述多次旋转时可以看作是多个旋转矩阵相乘是相同的。

本章的章节名是李群与李代数。那么什么是李群呢？

李群是具有连续(光滑)性质的群。类似于二维函数的连续。数学上已经证明SO(3)以及SE(3)都是李群。

在涉及一些优化问题时，我们需要对于旋转这一位姿变换进行求导操作来找出一些类似于"旋转的变化率"的概念帮助我们去优化。(如梯度下降)。但是对于SO(3)以及SE(3),仅满足乘法的封闭性，并不满足加法的封闭性，也就是并不处于线性空间中。如下导数的定义，显然想要求导且导数有意义的话，该代数结构应该在线性空间中才可以实现。

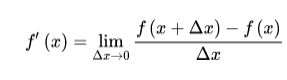
2. 李代数

对于R或者T来说，并不能直接对其求导，那么能否找到一种映射关系将其映射到线性空间中呢？

给出如下推导,假设旋转是随时间变化的函数。

\[\forall R(t)\in SO(3),R(t)R(t)^T = I \\ 两边求导(抽象的求导)得\\ \dot{R(t)}R(t)^T + R(t)\dot{R(t)^T} = 0 \\ 即\\ \dot{R(t)}R(t)^T = -R(t)\dot{R(t)^T} \\ 由 (ab)^T = b^Ta^T \\ \dot{R(t)}R(t)^T = -(\dot{R(t)R(t)^T})^T \\ 对于一个反对称矩阵，有 a = -a^T，显然上式满足，故\dot{R(t)}R(t)^T为反对称矩阵。\\ 假设 \dot{R(t)}R(t)^T = \phi(t)^\wedge \]

需要注意的是，这里的\(\phi(t)^{\wedge}\)中的^代表着一个三维向量\(\phi\)扩充为一个反对称阵。比如

\[a = (1,2,3)^T \\ a^{\wedge} = \begin{bmatrix} 0&1&2 \\ -1&0&3 \\ -2&-3&0 \\ \end{bmatrix} \]

因此\(\phi(t)^{\wedge}\)代表我们假设R由\(\phi\)扩充而来。
接着推理有

\[两边右乘R，有 \dot{R(t)} = \phi(t)^{\wedge}R(t) \\ 假定t = 0时刻 R = I，且认为t = 0附近\phi(t)变化不大，记作\phi_0\quad可认为上式就是一个微分方程。\\ 解得 \ln(R(t)) = \phi_0^{\wedge} \\ 同理有 R(t) = exp(\phi_0^{\wedge}) \]

可以看出，经过一通推导，我们发现旋转矩阵与一个东西有着对数形式上的映射。这里的\(\phi_0\)就是SO(3)对应的李代数。
与李群一样，李代数的构成也要满足一定的性质。如下

可以知道对于\(\phi_0\)来说，满足如上的定义

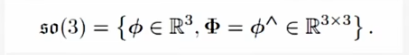
其李括号的定义的运算类型为

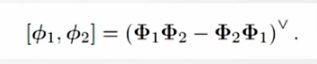
对于SE(3)上的李群，直接给出其李代数对应形式

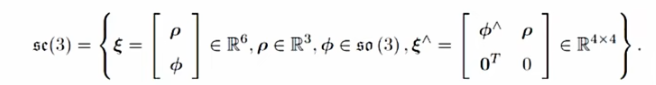
其李括号的定义为

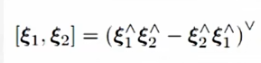
这里的\(\wedge\)操作与so(3)的定义不同，不再表示由三维向量扩充反对称阵，而是表示将\(\xi\)这个六维向量扩充为一个四维矩阵。不难看出\(\xi\)的前三维由平移向量得出，后三维就是se(3)。

数学上已经证明，李代数处于线性空间中，可以进行求导操作

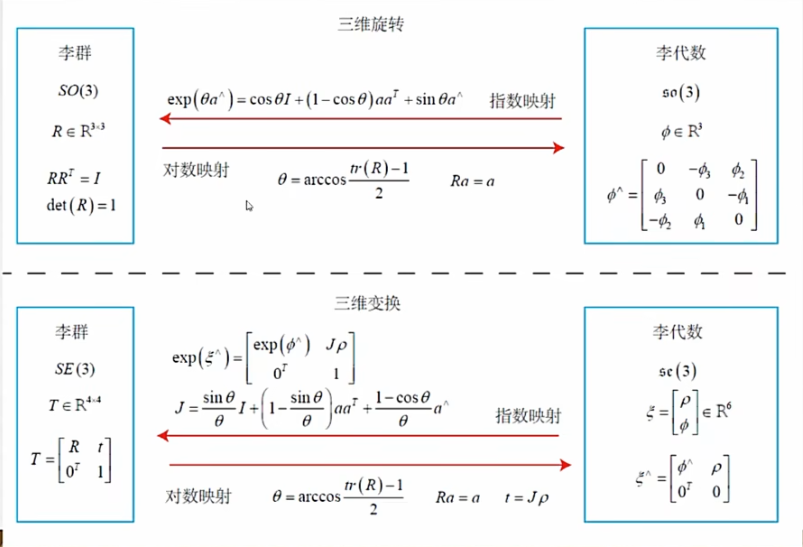
3. 对数映射与指数映射

上面我们给出了李代数与李群的映射关系，即

\[\ln(R(t)) = \phi_0^{\wedge}\\ 即 \ln{R(t)}^{\vee} = \phi_0 \\\ R(t) = exp(\phi_0^\wedge) \]

但是这只是抽象的公式，并没有告诉我们如何将其中的一些具体元素对应转换。但是通过这个我们可以知道对于已知李群求李代数是一种对数映射，已知李代数求李群是一种指数映射。

\[对于exp(\phi^{\wedge})，进行泰勒展开 \\ 因为e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots \\ 又对于一个三维向量可以写成模长乘单位方向向量的模式，不妨假设\phi = \theta\vec{a},\vec{a}为单位向量 \\ \]

具体形式与化简如下图

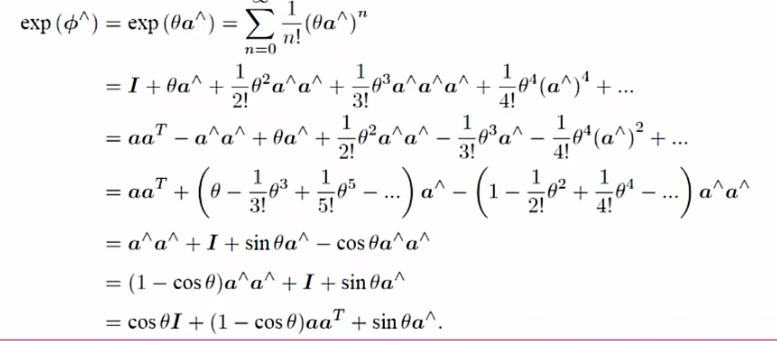
化简应用的性质如下

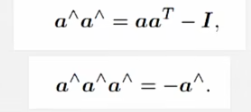
最终我们得出这样的一个式子

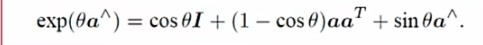
不难看出，这个公式与上一讲旋转矩阵转角轴(旋转向量)的罗德里格斯公式如出一辙。这也揭示了so(3)的物理意义就是旋转向量。

因此由so(3)的李代数指数映射求其对应的李群SO(3)的过程本质上就是旋转向量向旋转矩阵的转换。

对于已知旋转矩阵求其so(3)上的李代数的过程，我们有对数映射形式\(\ln{R(t)} = \phi\),尽然可以使用与求指数映射形式类似的泰勒展开来推导，这样比较麻烦。

但是我们已经知道了so(3)上的李代数实际上就是角轴，因此使用第三章中旋转向量转角轴的公式即可。

\[\text{角度}\\ \theta = arcos(\frac{tr(R)-1}{2})\\ \text{轴向量}\\ R\vec{n} = \vec{n}，求解R特征值为1时的特征向量 \]

关于方向向量的求解，因为使用角轴描述旋转时，旋转前后的单位方向向量是不变的(因为是绕着这个轴转的嘛)。因此对轴乘以旋转矩阵进行旋转操作后的结果仍是其本身，依据这个列出的特征方程。

至于SE(3)与se(3)之间的转换，由下图总结给出

最后总结以下李群与李代数的映射关系以及变换

4. 李群与李代数的近似

既然李代数处于线性空间，而且李群与李代数可以通过指数映射以及对数映射进行转换，那么我们是否可以直接使用李代数表述李群的求导操作呢？

一个朴素的思想

\[对于R_1R_2 = exp(\phi_1^\wedge)exp(\phi_2^\wedge) \\ 在实数域中有exp(x_1)exp(x_2) = exp(x_1 + x_2) \\ 猜想：是否有 R_1R_2 = exp(\phi_1^\wedge)exp(\phi_2^\wedge) = exp(\phi_1^\wedge + \phi_2^\wedge) = exp((\phi_1 + \phi_2)^\wedge) \]

但是根据BCH近似公式

可以知道对于两个矩阵，\(exp(A)exp(B) \neq exp(A+B)而是等于exp(A+B+余项)\)。

不过根据如下公式可以将上式进行线性近似

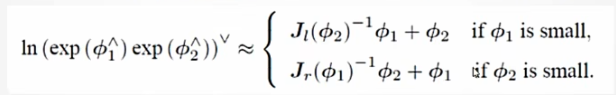
其中\(J_l\)为左乘雅可比矩阵，\(J_r\)为右乘雅可比矩阵。具体表示方法如下

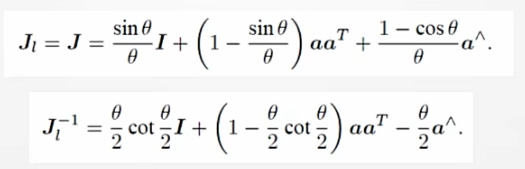
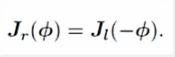
也就是说当两个量中有一个为小量时可以使用BCH近似来实现李群乘法转化为李代数加法。但是还是不够直观，给出如下推导。注意雅可比矩阵视为常系数。

\[exp((J_l(\phi_2)\phi_1)^{\wedge})exp(\phi_2^{\wedge}) = exp(J_l(\phi_2)(\phi_1)^{\wedge})exp(\phi_2^{\wedge}) \\ 根据以上BCH近似将J_l(\phi_2)(\phi_1)^{\wedge}看作小量，有 \\ exp(J_l(\phi_2)(\phi_1)^{\wedge})exp(\phi_2^{\wedge}) = exp(J_l^{-1}(\phi_2)J_l(\phi_2)\phi_1^\wedge+\phi_2^\wedge) = exp(\phi_1^\wedge + \phi_2^\wedge) = exp((\phi_1 + \phi_2)^\wedge) \]

即最后得出了这样一个等式,且将\(J_l(\phi_2)\)简写为\(J_l\)

\[exp((\phi_1+\phi_2)^\wedge) = exp(J_l\phi_1^\wedge)exp(\phi_2^\wedge) \]

依据这个等式，我们就可以将李代数的加法与李群的乘法近似且简洁的联系在一起了。下面贴出SE(3)与se(3)的关系，推导类似。

5. 李代数求导

以上我们就已经具备了实现李代数求导的准备。

求导的方法有两种

• 李代数求导
• 扰动模型求导
  对于旋转矩阵求导的应用场景如下

\[对于一个三维向量\vec{p},对其进行旋转操作R，求旋转后的向量或者点相对于旋转的变化率 \\ 不妨记为\frac{\partial{Rp}}{\partial{R}} \]

李代数求导

李代数求导就是将上式中的旋转矩阵李群直接用对应的李代数来进行替换，然后在李代数中套用导数定义来实现

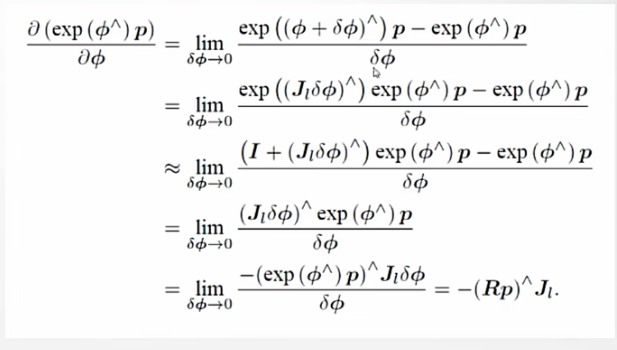
• 第二步使用了上面推导的\(exp((\phi_1+\phi_2)^\wedge) = exp(J_l\phi_1^\wedge)exp(\phi_2^\wedge)\)
• 第三步近似，因为\(J_l\delta\phi^\wedge\)是一个小量，因此由泰勒展开或者说等价无穷小，\(e^x = 1+x\)有\(J_l\delta\phi^\wedge = (I + (J_l)\delta\phi^\wedge)\)
• 第四步展开括号或者提公因式可以得出
• 第五步由反对称阵与向量叉乘的关系\(\vec{a}\times\vec{b} = \vec{a}^\wedge\vec{b} = -\vec{b}\times\vec{a} = -\vec{b}^\wedge\vec{a}\) 即 \(\vec{a}^\wedge\vec{b} = -\vec{b}^\wedge\vec{a}\)
• 第六步上下约掉\(\delta\phi\)

扰动模型求导

扰动模型求导的思路是在原来的旋转矩阵上左乘一个小的扰动旋转。然后对这个扰动求导。
不严谨的表示为

\[\lim_{\Delta R\rightarrow0}\frac{\Delta RRp-Rp}{\Delta R} \]

要做的就是将上述中的李群换成对应的李代数。设\(\Delta R\leftrightarrow \delta\varphi\),推导如下图。

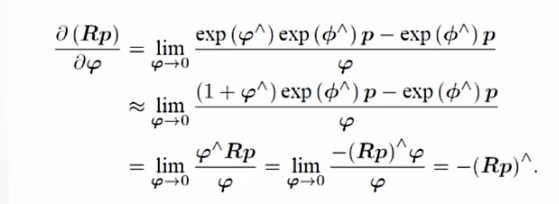
推导所使用的化简方法与李代数求导并无二异。
可以看出，使用扰动求导的方法得出的结果更加简洁，没有最后的左乘雅可比矩阵。

但是使用两种方法求出的结果是有差异的。

• 李代数求导的对象是对旋转矩阵本身，令导数等于0求出的旋转矩阵即为最优的旋转。
• 扰动模型求导的对象是\(\Delta R\),令导数等于0求出的为最优的\(\Delta R\),最终的\(R = \Delta RR\)

最后贴出SE(3)求导的推导。

需要注意的是\((Tp)^\odot\)中的\(\odot\)符号代表着SE(3)求导。

最后想要支持李代数李群相关运算，可以使用Sophus库来实现，Sophus库是Eigen的一个关于李代数李群的一个扩展库。