图(树)的深度优先遍历dfs
图的深度优先遍历
深度优先,即对于一个图或者树来说,在遍历时优先考虑图或者树的单一路径的深度。示意图如下
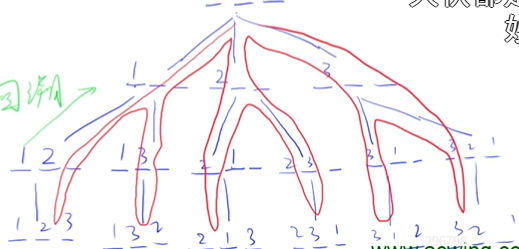
即深度优先搜索的核心就是对一个路径一直向下搜索,当搜索到头时就回溯到前一状态再寻找别的路
深搜问题一般有两种情况,一种是搜索时元素只能用有限次,这需要我们定义一个全局标记数组来对已经使用的数字进行标记。
如该题 排列数字
这道题的解法就是使用dfs枚举各种情况。当dfs时,其实就是在遍历一棵使用递归建成的搜索树。
题解代码如下
#include <iostream>
using namespace std;
const int N = 20;
int ans[N]; //答案存储数组
int n;
int cnt; //答案个数记录,用于写递归出口
bool check[N]; // 标记
void dfs()
{
if(cnt == 3)
{
for(int i = 0 ; i < 3 ; i++)
cout << ans[i] << ' ';
cout << '\n';
return;
}
for(int i = 1 ; i <= n ; i++)
{
if(!check[i])
{
ans[cnt++] = i;
check[i] = true;
dfs();
/*回溯*/
check[i] = false;
cnt --;
}
}
}
int main()
{
cin >> n;
dfs();
return 0;
}
注意!当dfs时一定别忘了写递归出口,递归出口的条件一般就为题目要求的筛选条件
dfs函数中的for循环其实就是枚举每一层的各种情况。
其实本道题还有更为方便的解法,利用algorithm库中的next_permutation函数可以轻松的解决字典序全排列问题。
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 20;
int ans[N]; //答案存储数组
int n;
int main()
{
cin >> n;
for(int i = 0 ; i <= n ; i++ )
ans[i] = i + 1;
do
{
for(int i = 0 ; i < n ; i++)
cout << ans[i] << ' ';
cout << '\n';
}while(next_permutation(ans, ans+n));
return 0;
}
该函数的作用请见next_permutation


 浙公网安备 33010602011771号
浙公网安备 33010602011771号