差分

AcWing笔记 - 差分

前言

求一个数组的差分，实际上是求前缀和的逆运算。
如给定数组A[N]，我们称使得A[i] = B[1] + B[2] + ..... + B[i]的B数组称为A数组的差分
显然A数组即为B数组的前缀和。

关于前缀和，可以看这篇前缀和 - 凪风sama - 博客园 (cnblogs.com)

前缀和主要用来优化的操作如下。对于数组A，要求进行多次如下操作：对于给定区间\([i,j]\)以及常数c，将数组A从 i 到 j 的所有元素都加上c。

• 若遍历 i 到 j ，则n次操作的时间复杂度为O(N²)数量级
• 若采用差分数组，我们仅需要对差分数组进行多次O(1)复杂度的操作，然后通过求前缀和求出原数组A，总的时间复杂度为线性。

\(1.\) 一维差分

还是先考虑一维数组情况下的差分。
这里给出原数组A，并将数组A从 i 到 j 的所有元素都加上c，求一次操作后的数组A

我们先构造假设出数组B为A的差分数组。由于A数组是B的前缀和，则A[ i ] = B[1] + .... +
B[i] ，同理 A[i+1] = B[1] + .... + B[i] +B[i+1]，一直到A[j] = B[1] + ... + B[i] +... +B[j] 。

可以看出，从 i 到 j ，由于A为B的前缀和，故若要将 i - j 的元素都加上c ，则只需要将B[i]加上c即可，这样用B数组求出的前缀和A，从第 i 项开始都会比原来多c。

但是我们要的是 i - j 加 c，所以从 j 往后的元素不应该加c，因此我们让B[j+1]减去c，这样再求前缀和的时候，只有从 i - j 的元素加了c，其他元素不变。

我们将这种对B数组的操作写成一个函数

void Insert(int i,int j,int c)
{
	B[i] += c;
	B[j+1] -= c;
}

现在回到最初的问题，对于给定的原数组A，如何求其差分数组B？

其实，我们可以想象A数组原先是一个所有元素都为0的数组记为A₁，自然其对应的差分数组也都为0。

而由A₁到A，不过是在每个长度为1的区间内执行了插入操作。也就是说对于A₁[i]
到A[i]，在其差分数组层面，执行的是

Insert(i, i, c)

其中c为A[i]的值。
由此，我们遍历A[i]，对空数组B执行n次长度为1的插入操作，就可以得到A数组的差分数组B了。

接着再根据题目要求对相应的区间进行B的插入操作。最后对B求一次前缀和就可以得到操作过后的A数组了。

\(1.\) 二维差分

类比一维差分，二维差分就是给出原数组A，构造出数组B，使得A是B的二维前缀和，即A[i][j] = B[1][1] + ....+ B[i][j]。

同理，这里我们要解决的问题为

给出原二维数组A[N][M]，我们对其进行n次操作，操作为在以(x1 , y1) 以及 (x2 , y2)为对角点的矩形区域内的所有A[i][j]加上常数c。

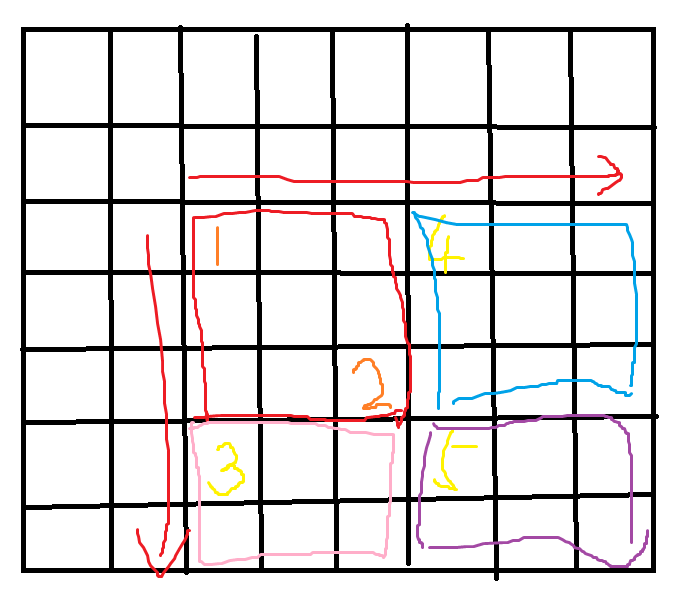
如上图，每个格子代表差分数组B的一个元素。设1为(x1 , y1) ，2为（x2 ，y2）。
可以知道，若想让A[x1][y1]之后的元素全都加上c，那么只需要让B[x1][y1]加上c即可。

但是考虑到我们只要矩形区域的前缀和加上c，因此为了防止矩形外的前缀和也加上c，我们做如下处理。

3位置(x2+1, y1)元素减c
4位置(x1 . y2+1)元素减c
由于计算右下角的前缀和时，1位置加c，3，4位置减c，因此为了不变，要求5位置(x2+1 ,y2+1)加c

综上得出二维差分数组的插入操作即为

void Insert(int x1, int y1, int x2, int y2, int c)
{
	B[x1][y1] += c;
	B[x2+1][y1] -= c;
	B[x1][y2+1] -=c;
	B[x2+1][y2+1] +=c;
}

同理，若仅求原数组A的差分数组B，可以仿照一维差分的单区间插入，仅插入一个格子，例如对于A[i][j]

Insert(i, j, i, j, c)

其中c为A[i][j]的值

求出B后再根据题目进行插入操作即可。别忘了操作过后求出B的前缀和，来得到加c操作后的A数组