洛谷P1102 过河卒

P1102 过河卒

链接在此
过河卒
此题如果直接忽略掉马🐎的影响的话，可以看出很简单的递推规律
即

\[dp[i][j]=dp[i-1][j]+dp[i][]j-1] \]

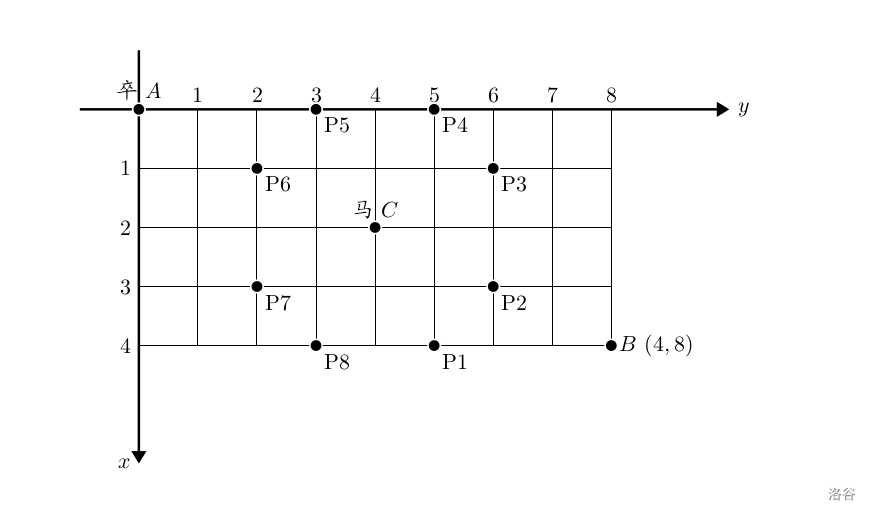
也就是说，由于卒只能走直线且每次只能向下或向右走一步，那么，要到达第（i，j）点，卒只能从（i-1，j）点以及（i，j-1）这两个点来达到。因此，卒走到第（i，j）点的路径条数即为卒走到第（i-1，j）以及（i，j-1）点的路径条数和，以此类推，因此只需要初始化初值条件就可以推出答案

但是这里我们加上了一个限制条件，也就是马能触及到的地方不能走，当然🐎所在的地方更不能走（容易忘）
所以我们在原先的递推上将这些点标记起来(可以用一些特殊值如-1或者开个bool数组来进行标记)，当递推的时候我们直接略过这些点

举个例子

对于点（2，2），\(dp[2][2]=dp[1][2]+dp[2][1]\),但是明显点（1，2）是不可经过的点，因此\(dp[2][1]\)应该恒等于0，因为没有任何一条路径会经过它。所以此时\(dp[2][2]=dp[1][2]\)

AC代码如下

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int offsetx[8] = { +2,+1,-1,-2,-2,-1,+1,+2 };
const int offsety[8] = { +1,+2,+2,+1,-1,-2,-2,-1 };
//马偏移量记录
long long Map[30][30];
//结果记录，不开longlong会爆掉
int main()
{
	int x1, y1, x2, y2;
	cin >> x1 >> y1 >> x2 >> y2;
	for (int i = 0; i < 8; i++)
	{
		int x = x2 + offsetx[i];
		int y = y2 + offsety[i];
		if (x >= 0 && y >= 0 )//保证不出界
			Map[x][y] = -1;
	//这里采取将所有不可经过点标记为-1
	}
	if (x2 >= 0 && y2 >= 0)//马所在的那个点也要标记-1
		Map[x2][y2] = -1;
	for (int i = 0; i <= x1; i++)
		if (Map[i][0] != -1)
			Map[i][0] = 1;
		else
			break;
	for (int i = 0; i <= y1; i++)
		if (Map[0][i] != -1)
			Map[0][i] = 1;
		else
			break;
	//以上两步是将dp数组的边界初始化为1(很容易想到边界的值都为1)
	//但是要注意一旦遇到不可经过点处于边界上时，此后的Map[i][j]一律为0
	//因为对于边界点Map[i][0](Map[0][i])=Map[i-1][0],而如果(i-1,0)这个点为-1，意味着无法经过这个点到达后面的点，因此此时Map[i][0]=0
	for (int i = 1; i <= x1; i++)
		for (int j = 1; j <= y1; j++)
		{
			if (Map[i][j] != -1)//跳过不可经过点
			{
				if (Map[i - 1][j] != -1)//判断是否为-1
					Map[i][j] += Map[i - 1][j];
				if (Map[i][j - 1] != -1)
					Map[i][j] += Map[i][j - 1];
			}
		}
	cout << Map[x1][y1] << endl;
	return 0;
}