记忆化搜索 P1028 数的计算

P1028 [NOIP2001 普及组] 数的计算 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

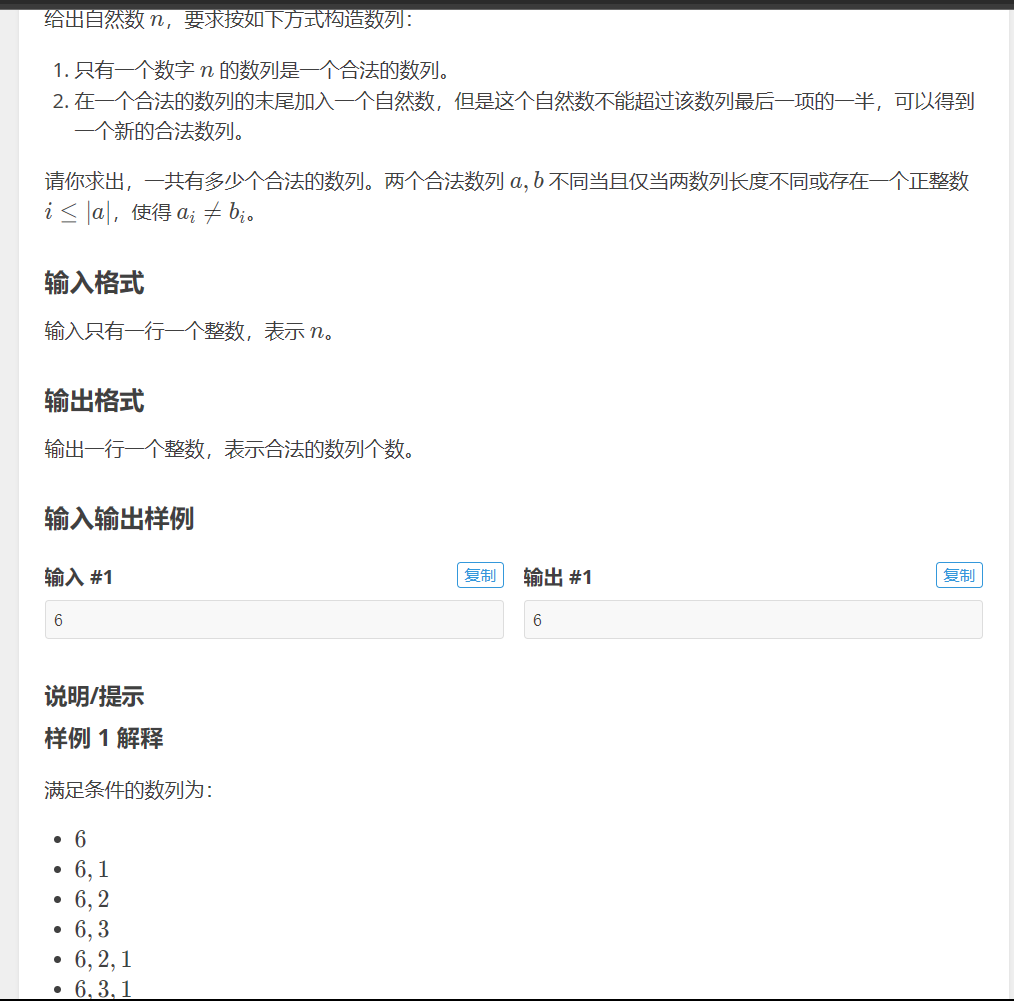
一开始是想暴力搜索的，也就是枚举比n/2小的数，但是只过了5个点，其他点都TLE

然后就开始想有没有优化方法

以6为例子

6/2=3，那么以6为首的长度为2的序列就有61，62，63，也就是所有小于等于3的数的个数

接下来，我们找长度为3的序列的个数，只需要关注第二位的数字即可， 也就是说只需要找到以1，2，3为首的序列的个数相加即可

至此可以知道N[6]=N[3]+N[2]+N[1]+1;同理，N[3]=N[1]+1,N[2]=N[1]+1,N[1]=1;

这里的加1指的是只有首元素的序列，由此我们可以得出N[k]=N[1]+N[2]+......+N[k/2]+1的递推公式，这样递推下去，知道推到初始值N[1]=1就可以得出答案了

同时防止重复计算某个位置的值，采用记忆化搜索策略，否则还是会TLE

AC代码

 

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int cnt = 1;
int dp[1010] = { 0 };
int Solve(int n)
{
    
    if (dp[n] == 0)//当此位置为被计算过才进行计算后返回，否则直接返回
    {
        if (n == 1)
        {
            dp[n] = 1;
            return dp[n];//边界返回
        }
        for (int i = 1; i <= n / 2; i++)
        {
            dp[n] += Solve(i);//累加
        }
        dp[n] += 1;
    }
    return dp[n];
}
int main()
{
    int n;
    cin >> n;
    Solve(n);
   cout << dp[n];
}