快速幂结合取模运算

先贴一个快速幂模板

long long int quik_power(int base, int power)
{
    long long int result = 1;
    while (power > 0)           //指数大于0进行指数折半，底数变其平方的操作
    {
        if (power & 1)            //指数为奇数，power & 1这相当于power % 2 == 1
            result *= base;     //分离出当前项并累乘后保存
        power >>= 1;            //指数折半,power >>= 1这相当于power /= 2;
        base *= base;           //底数变其平方
    }
    return result;              //返回最终结果
}

转载至(24条消息) 快速幂算法 超详细教程_qascetic的博客-CSDN博客

相信你对这个模板已经很熟了，那么我们来使用快速幂加上取模运算来求一些比较大的幂mod一个数的问题

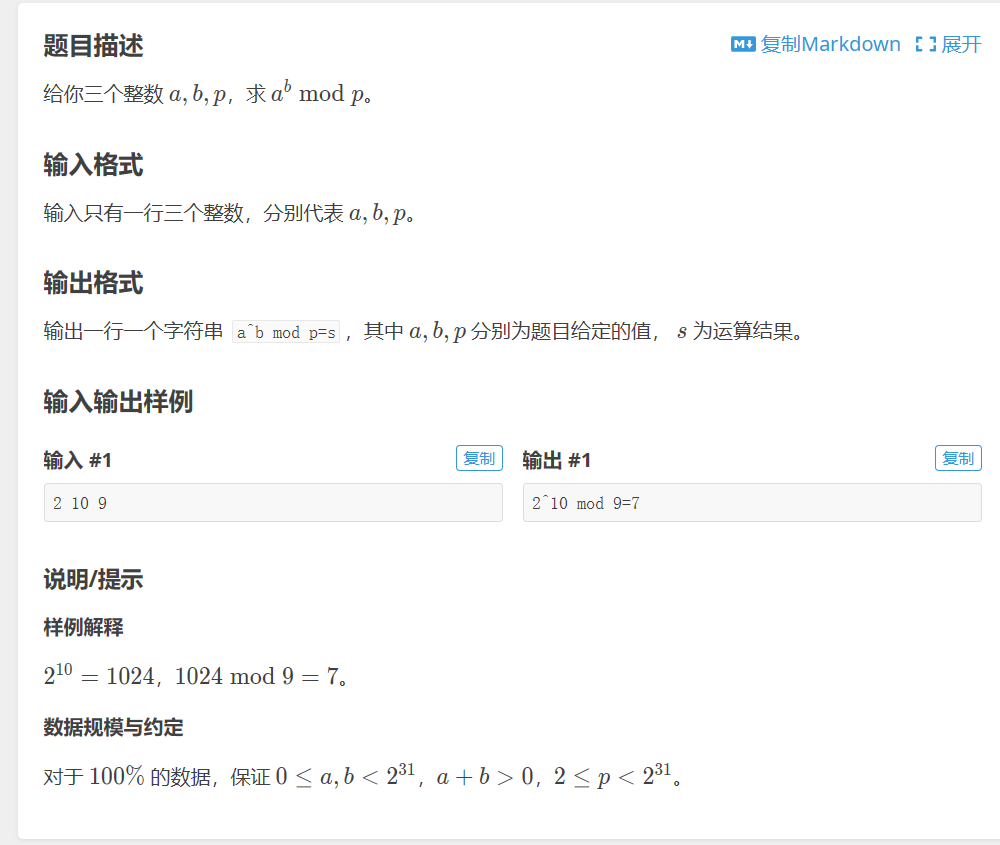
 可以看到a，b，p都是比较大的，为了防止爆int，我们要在快速幂的同时进行取模运算，即每次快速幂都进行取模，防止超出int范围

下面给出几个取模运算的公式

1. (a+b)%p=(a%p+b%p)%p
2. (a-b)%p=(a%p-b%p)%p
3. (a*b)%p=(a%p * b%p)%p

由此，对于每次快速幂都是一个乘法，因此可以借用第三条公式加入我们的快速幂模板中变为如下

int P;
cin>>P;
long long int quik_power(int base, int power)
{
    long long int result = 1;
    while (power > 0)           
    {
        if (power & 1)          
            result =result*base%p;     
        power >>= 1;           
        base =base*base%P;         
    }
    return result%P;            
}

 对于快速幂，借用二进制，可以看为  N^1 * N^2 * N^4 * N^8 * N^16 * ....* N^2*n-1,

在进行取模，采用二分的思想，可以知道总结果就是每个步骤加上最后的返回步骤都要取模