杨辉三角递推公式

 

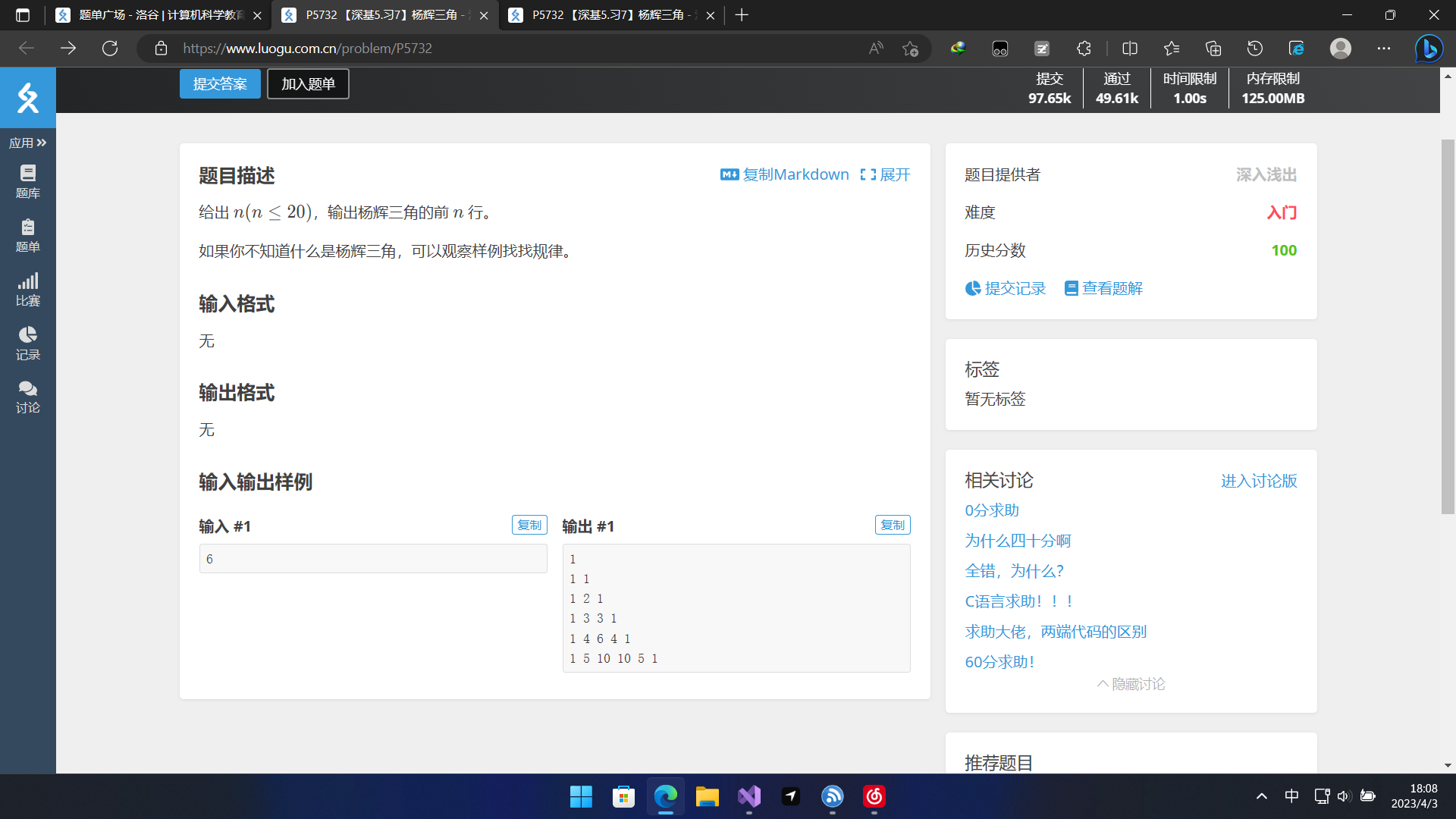
  对于一个二维数组来说，我们用真实下标来表示数组下标，即下标从1开始而非从0开始

那么对于杨辉三角数组的元素a[i][j]=a[i−1][j]+a[i−1][j−1]，其中初值条件为a[i][1]=1（即最前列全置1）,a[i][i]=1（最后列全置1）,

然后通过一个嵌套循环即可计算得出

 

for(int i=3;i<=n;i++)//直接从第三行开始，前两行已经由初值条件决定好了

{

for(int j=2;j<=i-1;j++)//从第二列开始，到倒数第二列结束，对于每一行其列数等于行数

{

a[i][j]=a[i-1][j-1]+a[i-1][j];

}

}//复制过来的，可能不太好看

 

 

 

当然也可以将数组定义为全局变量或者初始化为0，这样初值只需要让a[1][1]=1,即可（下标依旧从1开始）

如下

#include<cstdio>
int n,a[21][21];
int main()
{
    scanf("%d",&n);//输入
    a[1][1]=1;//初始化
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
            a[i][j]=a[i-1][j-1]+a[i-1][j];//进行计算
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++)printf("%d ",a[i][j]);//输出
        printf("\n");//换行
    }
    return 0;
}

 当然这道题也可以用组合数计算来得出，但是组合数的计算涉及阶乘，因此很容易越界，不过这道题只需要到20的阶乘，用long long就可以了（用int确实会超）

如下

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int Get_Cxy(int x, int y)//计算组合数，x是下面的，y是上面的
{
    long long X = 1;
    for ( int i = x; i > x - y; i--)
    {
        X *= i;
    }
    long long Y = 1;
    for (int j = y; j >= 1; j--)
    {
        Y *= j;
    }
    return X / Y;
}
int main()
{
    int n;
    scanf("%d", &n);
    for (int i =0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
            if (j == 0)
                printf("%d", Get_Cxy(i, j));
            else
                printf(" %d", Get_Cxy(i, j));
        printf("\n");
    }
    return 0;
}