最小树形图
好像是一个OI中应用不是很多(不要打脸)的算法
算法
朱刘算法了解一下本文就是讲这个的......
其实主要是我调了很久一道题,然后发现一个智障错误然后过来写博客
算法主要解决有向图最小生成树问题.
定义
在一个有向图中选择一些有向边集构建一颗树,然后使这棵树的边权和最小。
就是根确定的“最小有向生成树”。
前面的东西
Q:如何判断存在性?
A:直接拿着根跑dfs即可。
注意这是一个比较重要的地方无解的情况下会有几个点没有入度,然而这样是非法的,同时我们筛掉这种情况之后可以保证只有一条入边的最小树形图是最优的而且合法的(如果有两条入边要么可以删掉一条要么是无解情况)
Q:复杂度?
A:$O(VE)$
我们认为根$Root$一开始已经给定(后面会将没给定的特殊情况)。
记边权为$w$
以下的证明不一定会严谨......
算法
首先我们需要清除自环,因为存在自环的话会使复杂度增高但又没有意义。
操作一
对于除根以外的所有点选定一条入边,该条入边是所有入边中权值最小的一条。
定理一
上面的操作之后如果没有环的话那么就是最小树形图。
证明:
如果不是最小树形图的话那么一定存在一条边可以替代原有的边,但是由于原图已经是一棵树,所以替换一条边只可能:
- 破坏树的结构
- 换到了一条更大的边
所以并没有可以换的边。
然后如果没有环的话那么就直接跑路输出答案(等下介绍缩了环之后的答案怎么计算),如果有呢?
如果存在一个环的话,那么我们这样做缩环:
操作二
这一操作命名为缩环(自己瞎BB的)。
令环上任意一点$u$,指向它的有向边为$v$点,令$u$和$v$之间的边的边权为$ind[u]$,然后我们新建了一个节点$p$代替这个环,并且与外界有如下联系:
对于点$u$的入边(起点为$s$)连接$s$到$p$,边权为$w-ind[u]$
对于点$u$的出边(起点为$t$)连接$p$到$t$,边权为$w$
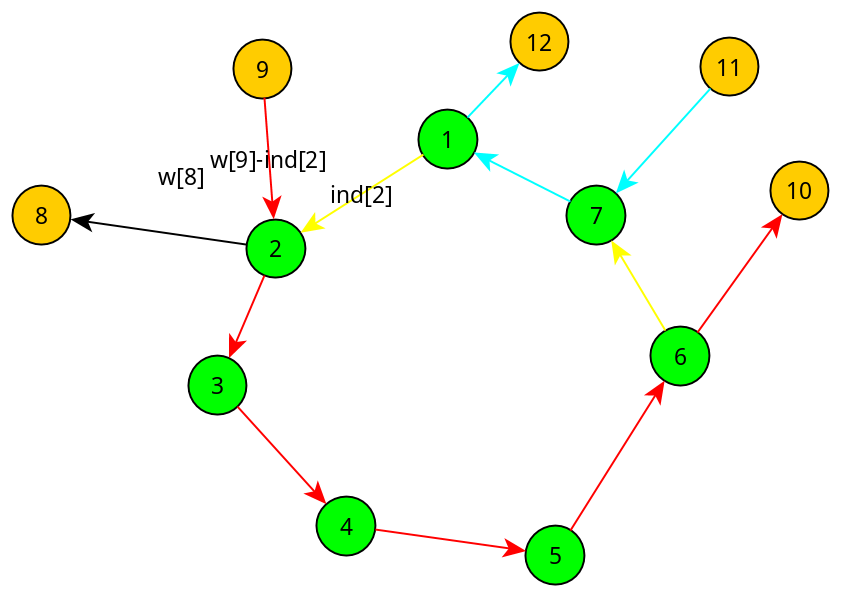
例如下面这幅比较原谅的图,假设所有绿色的点为新点$p$所代表的点。左上角的连边说明了一个实例。
定理二
对于上面的操作,当前这一层的最小树形图=缩环后的最小树形图+环内权值
证明(解释为什么要在缩环的时候换边权):
由于生成树要求每一个点都要走到,包括环内的点,所以最后的答案肯定长成这张图的样子(解释),即对于一个环在最终的答案中会被选到的只会有环的 $边数-1$、$一条入边$ (为什么只有一条边:因为缩了环之后的图和原图的入边一一对应,而根据最小树形图的算法流程,我们每次只会选择缩了环之后的图的缩点的一条入边作为答案,所以对应到原图也只有一条边)而可能有 $几条出边$ 。我们发现环内的1条边肯定是走不到的,也就是图中的黄色边(如果$9->2$是入边则为$1->2$这条边,如果$11->7$是入边则$6->7$选不到),也就是$v$到$u$的边,边权为$ind[u]$。也就是说如果有一条路径从$u$进入了这个环,那么环内$v$到$u$的边就会不在生成树中。
所以我们只需要在入边的$w$上减去$ind[u]$即可保证这条的排名以及在最终对答案产生的贡献正确。
最后我们只需要递归地跑算法即可。
然后为什么这样递归下去最后得到的一定是最小值呢?
定理二的最优性证明
感谢@ Rite的提醒,大概我是只考虑到了自己不熟悉的地方吧,以后写的时候的确要注意一下
(虽然我有点没有看懂评论)
首先定理一讲述了在没有环的情况下为什么是最优的,大致就是一个反证吧。
然后另一部分我们干脆加入一个定理三:
定理三
一张图缩了环之后的最小树形图就是缩环前的最小树形图
首先我们考虑到一个环在最小树形图代表的一个缩掉之后会长什么样子

先不考虑蓝色边
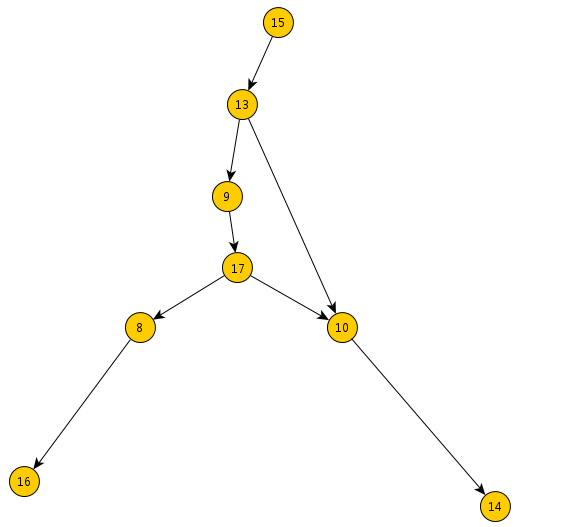
然后由于整个环内的所有点都必须选到,所以这个环在相当于选择了一条入边之后有些边是一种“必选”,也就是无论如何都必须跑完所有点,同时不管缩了环的图有多少入边出边都如此,最后缩了环的图肯定只有只有一条入边,所以其实环的边的选择在选择了入边之后是固定的
例如正上方的原图中我们可以选择走$6->10$的边来走到10或者走$13->10$的边来走到10,但是我走到环内的任何一个点它就只能从某个入口进来,然后沿着环走遍历点,可以选的就只有入口之后的点。例如最上面的图,$6->7$黄色边有可能有选择的机会,然后我们处理了这种边的选择然后再缩点,相当于我得到了一个答案之后然后直接在答案上加一些不影响的答案选择的边,因为这些边必须选择,所以必须加入答案。
我们用一个公式表达一下
定义$e\ in\ loop$表示环内的边,$in$表示入边,$out$表示出边,$pre$表示环内的不要选的边,$Ans'$表示缩了环之后的图除了被缩环的点周围的边的答案
$Ans = Ans' + \Sigma{w_{e\ in\ loop}} + w_{in} - w_{pre} + \Sigma{w_{out}}$
可以发现右边第一项第二项会不受环的影响,必须累加在答案中,然后$\Sigma{w_{out}}$不会受入边的影响,根据自己的边权决定答案
然后$w_{in} - w_{pre}$需要配套选择,所以我们把它集中在了一条边上选择
所以在$Ans'$最优下$w_{in} - w_{pre}$和$\Sigma{w_{out}}$选择最小边即可
然后一种更复杂的情况:环套环
就是加了那种蓝色边的
但是由于你会跑一次这个环去找环的边,所以其实你首先会找到并且缩掉那个小环,这个时候长这样,然后就只剩下一个环了
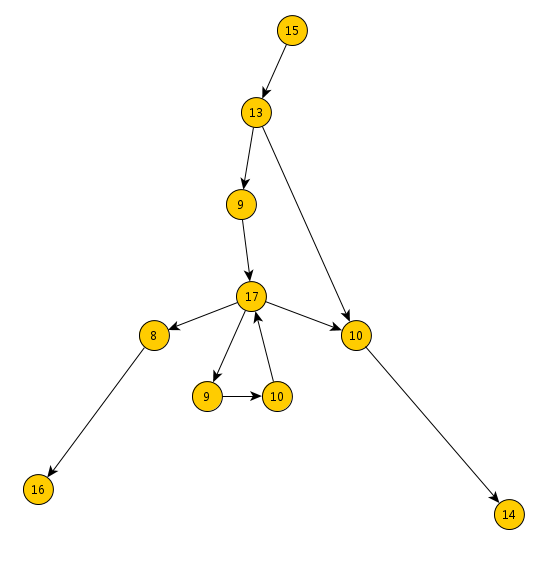
其实问题等价
还原
当你递归下去求得答案之后怎么还原选择的边呢?
除了被缩成点的环缩代表的点之外的点之间相连的边都是最终的答案
首先在上面我们认识到
- 一个环只会有一条入边
- 在这条入边后面(上面有说这条边是什么)的环上的一条边不会被选
所以我们还原完正常的边之后然后还原环内除了“后面”的那条边即可
复杂度组成
每次找最小边$O(E)$,缩点$O(V)$,更新边$O(E)$,由于删掉了自环,所有每次至少删掉一个点,所以递归层数$O(V)$
总复杂度$O(VE)$
后面的东西
如果我这个虾皮出题人没有指定根怎么办?让你去枚举根?
那么我们可以建立虚拟根$root$(小写),然后向每个点连出$S>\Sigma{W_i}$的边,然后再跑,最后答案减去S即可。
但是有一种情况就是发现减了之后答案还是大于$S$,那么这说明原图不连通(因为如果连通的话肯定算法不会智障到去选边权为S边)
然后我们找到的最小边的和$root$相连的点就是最小根。
例题
Luogu P2792 [JSOI2008]小店购物
题意
就是去交易买东西,一些货物有原价,如果你先买$x$货物然后再买$y$货物搞不好就有优惠 (
( )。
)。
你需要为每一种物品不多不少选$k_i$件。
题解
考虑到如果我们选择最优方案,那么只有第一个物品是需要考虑折扣的,后面的物品可以直接选取最便宜的。
首先统计后面优惠价的所有答案。
我们为每一个物品都开一个节点,然后再开一个$root$, 从$root$向物品连边,权值为原价
然后对于每一对优惠$x$对$y$,从$x$向$y$连边,边权为折扣价。
最后跑一边算法然后累加到原来的答案内即可。
一开始我的板子出了一个非常......的错误,然后调了几年,然后又被卡精度......
代码如下:

1 #include <cstdio> 2 #include <cctype> 3 #include <cassert> 4 #include <cstring> 5 6 #include <fcntl.h> 7 #include <unistd.h> 8 #include <sys/mman.h> 9 10 //User's Lib 11 12 using namespace std; 13 14 char *pc; 15 16 inline void Main_Init(){ 17 static bool inited = false; 18 if(inited) fclose(stdin), fclose(stdout); 19 else { 20 #ifndef ONLINE_JUDGE 21 freopen("b.in", "r", stdin); 22 freopen("b.out", "w", stdout); 23 #endif 24 pc = (char *) mmap(NULL, lseek(0, 0, SEEK_END), PROT_READ, MAP_PRIVATE, 0, 0); 25 inited = true; 26 } 27 } 28 29 static inline int read(){ 30 int num = 0; 31 char c, sf = 1; 32 while(isspace(c = *pc++)); 33 if(c == 45) sf = -1, c = *pc ++; 34 while(num = num * 10 + c - 48, isdigit(c = *pc++)); 35 return num * sf; 36 } 37 38 static inline double read_dec(){ 39 double num = 0, decs = 1; 40 char c, sf = 1; 41 while(isspace(c = *pc ++)); 42 if(c == '-') sf = -1, c = *pc ++; 43 while(num = num * 10 + c - 48, isdigit(c = *pc ++)); 44 if(c != '.') return num * sf; 45 c = *pc ++; 46 while(num += (decs *= 0.1) * (c - 48), isdigit(c = *pc ++)); 47 return num * sf; 48 } 49 50 namespace LKF{ 51 template <typename T> 52 extern inline T abs(T tar){ 53 return tar < 0 ? -tar : tar; 54 } 55 template <typename T> 56 extern inline void swap(T &a, T &b){ 57 T t = a; 58 a = b; 59 b = t; 60 } 61 template <typename T> 62 extern inline void upmax(T &x, const T &y){ 63 if(x < y) x = y; 64 } 65 template <typename T> 66 extern inline void upmin(T &x, const T &y){ 67 if(x > y) x = y; 68 } 69 template <typename T> 70 extern inline T max(T a, T b){ 71 return a > b ? a : b; 72 } 73 template <typename T> 74 extern inline T min(T a, T b){ 75 return a < b ? a : b; 76 } 77 } 78 79 //Source Code 80 81 const int MAXN = 111; 82 const int MAXM = 555; 83 const int INF = 0x3f3f3f3f; 84 85 int n, m; 86 int ind[MAXN], pre[MAXN], id[MAXN], vis[MAXN]; 87 struct Edge{ 88 int u, v, w; 89 Edge(){} 90 Edge(int _u, int _v, int _w) : u(_u), v(_v), w(_w){} 91 }edge[MAXM]; 92 93 inline int MA(){ 94 int ret = 0, root = n, num; 95 while(true){ 96 memset(ind, 0x3f, sizeof(ind)); 97 for(int i = 1; i <= m; i++) 98 if(edge[i].u != edge[i].v && ind[edge[i].v] > edge[i].w) 99 ind[edge[i].v] = edge[i].w, pre[edge[i].v] = edge[i].u; 100 for(int i = 1; i <= n; i++) 101 if(i != root && ind[i] == INF) 102 return -1; 103 memset(id, -1, sizeof(id)), memset(vis, -1, sizeof(vis)); 104 num = ind[root] = 0; 105 for(int i = 1; i <= n; i++){ 106 int v = i; 107 ret += ind[i]; 108 while(vis[v] != i && v != root) 109 vis[v] = i, v = pre[v]; 110 if(v != root && id[v] == -1){ 111 id[v] = ++ num; 112 for(int j = pre[v]; j != v; j = pre[j]) 113 id[j] = num; 114 } 115 } 116 if(!num) return ret; 117 for(int i = 1; i <= n; i++) 118 if(id[i] == -1) 119 id[i] = ++ num; 120 for(int i = 1; i <= m; i++){ 121 int ori = edge[i].v;//ori 122 edge[i].u = id[edge[i].u], edge[i].v = id[edge[i].v]; 123 if(edge[i].u != edge[i].v) edge[i].w -= ind[ori]; 124 } 125 n = num, root = id[root]; 126 } 127 } 128 129 int cost[MAXN], ks[MAXN], pos[MAXN]; 130 131 inline void Re(int &tar){ 132 if(tar % 10 != 0){ 133 tar ++; 134 //printf("%d\n", tar); 135 } 136 } 137 138 int main(){ 139 Main_Init(); 140 n = read(); 141 for(int i = 1, j = 1; i <= n; i++, j++){ 142 Re(cost[i] = double(read_dec()) * 100.0), ks[i] = read(); 143 if(!ks[i]) i --, n --; 144 else ks[i] --, pos[j] = i; 145 } 146 n ++; 147 for(int i = 1; i < n; i++) 148 edge[++ m] = Edge(n, i, cost[i]); 149 int t = read(); 150 for(int i = 1; i <= t; i++){ 151 int x = pos[read()], y = pos[read()], w; 152 Re(w = double(read_dec()) * 100.0); 153 if(!(x && y)) continue; 154 LKF::upmin(cost[y], w); 155 edge[++ m] = Edge(x, y, w); 156 } 157 int ans = 0; 158 for(int i = 1; i < n; i++) 159 ans += cost[i] * ks[i]; 160 int ret = MA(); 161 assert(ret != -1); 162 printf("%.2lf", (ret + ans) / 100.0); 163 Main_Init(); 164 return 0; 165 }
参考文献|资料:
我也找不到原论文,算法是由朱永津与刘振宏提出的,对此表示敬意。
图是自己画的......



