浮点数的一点东西
从浮点的原理到表现在C++上的特性分析
主要参考《深入理解计算机系统》
前置声明
很久之前写完的,用Markdown转移过来发布了,有错误或问题请在评论区中指正
IEEE 754大法好
大端法小端法
然后声明一下测试环境
测试环境首先用
#include <cmath> #include <cstdio> #include <iomanip> #include <iostream> using namespace std; union test{ struct{ unsigned long long ulx1; unsigned long long ulx2; }b; long double a; }; void print_bit64(unsigned long long tar){ for(int i = 63; ~i; i--){ putchar(bool((tar >> i) & 1) + 48); } puts(""); } union DDF{ unsigned int a; unsigned long long b; void test(){ a = 0xffffffff; print_bit64(b); } }; int main(){ DDF().test(); test t; t.b.ulx1 = t.b.ulx2 = 0; t.a = INFINITY; cout << sizeof(t.a) << endl; cout << sizeof((&t)) << endl; # ifndef _WIN64 cout << (unsigned)(&t) << endl; cout << (unsigned)(&t.a) << endl; cout << (unsigned)(&t.b.ulx1) << endl; cout << (unsigned)(&t.b.ulx2) << endl; # else cout << (unsigned long long)(&t) << endl; cout << (unsigned long long)(&t.a) << endl; cout << (unsigned long long)(&t.b.ulx1) << endl; cout << (unsigned long long)(&t.b.ulx2) << endl; # endif print_bit64(t.b.ulx1); print_bit64(t.b.ulx2); return 0; }
测试机器用的是大端法还是小端法,并且测试float和double还有long double大小
大端法
小端法
大端法和小端法指的是字节在内存中存储时的排列规则,而不是数据中的位的排列规则。也有以位序排列的机器,但很少见。另外,再次明确一下,大端法或小端法是数据在存储时的表现,而不是在寄存器中参与运算时的表现。
在所有机器上,浮点数在存储时的字节顺序是和整数的字节顺序一样的,所以在进行网络传输时,可以把浮点数当作整数进行字节序转换。但在历史上,曾经有段时间因为 IEEE 并没有规定浮点数在网络上传送的标准,所以浮点数都是以大端法进行存储的。
(引用自Blog_Link)
然后我们测试的原理就是由于C++定义共用体的所有成员存放顺序从低地址开始,也就是这样一张图

那么我对unsigned的操作作用在unsigned long long的字节上的位置是由机器的大小端法决定的
然后我们就可以利用这个方便提取浮点数二进制
如何读这个二进制数?下一节有解释
关于研究对象
float和double还有long double在x86的NOI Linux(Gnu-Gcc-4.8.4, C++98)和x64的Windows10 19H1(MinGW-W64-Gcc-8.1.0, C++11)的表现
统称测试环境:前者为x84,后者为x64
x64下测试结果
0000000000000000000000000000000011111111111111111111111111111111
16
6422016
6422016
6422016
6422024
1000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000111111111111111
x86下测试结果
0000000000000000000000000000000011111111111111111111111111111111
12
18446744072632234784
18446744072632234784
18446744072632234784
18446744072632234792
1000000000000000000000000000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000111111111111111
特别注意long double:
With the GNU C Compiler, long double is 80-bit extended precision on x86 processors regardless of the physical storage used for the type (which can be either 96 or 128 bits)
这句话是什么意思?也就是说x86下的long double的有效位数只有80bit,不管储存的空间是96bit还是128bit,而且实际测试得到发现x64下编译出来的结果也是80bit,即使使用-m128bit-long-double参数
但是由上面的结果可以看出,long double在x86和x64下确实占用的空间不同
但是IEEE定义了所有的类型,并没有80bit,而80bit可以参考Link,对应的Extended_precision其实还有40bit的
下面的表有一些重要的信息在后面会用到
| Name | Common name | Base | Significand Bits[b]/Digits | Decimal digits | Exponent bits | Decimal E max | Exponent bias[10] | E min | E max | Notes |
|---|---|---|---|---|---|---|---|---|---|---|
| binary16 | Half precision | 2 | 11 | 3.31 | 5 | 4.51 | 24−1 = 15 | −14 | +15 | not basic |
| binary32 | Single precision | 2 | 24 | 7.22 | 8 | 38.23 | 27−1 = 127 | −126 | +127 | |
| binary64 | Double precision | 2 | 53 | 15.95 | 11 | 307.95 | 210−1 = 1023 | −1022 | +1023 | |
| binary80 | Extended precision | 2 | 63 | 19.26 | 15 | 4931.77 | 214−1 = 16383 | −16382 | +16383 | |
| binary128 | Quadruple precision | 2 | 113 | 34.02 | 15 | 4931.77 | 214−1 = 16383 | −16382 | +16383 | |
| binary256 | Octuple precision | 2 | 237 | 71.34 | 19 | 78913.2 | 218−1 = 262143 | −262142 | +262143 | not basic |
| decimal32 | 10 | 7 | 7 | 7.58 | 96 | 101 | −95 | +96 | not basic | |
| decimal64 | 10 | 16 | 16 | 9.58 | 384 | 398 | −383 | +384 | ||
| decimal128 | 10 | 34 | 34 | 13.58 | 6144 | 6176 | −6143 | +6144 |
浮点原理
前言废话
有时候会看到浮点数可以储存下比它们对应的整数还大的数值,例如1e10竟然可以存在32bit的float中!
然后就会有一种想法:能不能用它做高精度或者是大数取模呢?
好像在骆可强的《论程序底层优化的一些方法与技巧》提到了这回事
typedef long long ll; #define MOL 123456789012345LL inline ll mul_mod_ll(ll a,ll b){ ll d=(ll)floor(a*(double)b/MOL+0.5); ll ret=a*b-d*MOL; if(ret<0)ret+=MOL; return ret; }
这样也是可以的,但是前提是模数不能太大,因为a * b会出现乘法溢出,但溢出部分误差最多为1,会溢出到符号位上,所以特判符号位即可
正式开始
IEEE浮点标准使用$V = (-1) ^ s * M * 2 ^ E$的形式表达一个浮点数
- 符号(sign) s,记为$s = 0/1$,决定这个数是正数(s = 0)还是负数(s = 1),特别的,0有两种表达(0.00或者-0.00)
- 尾数(significand) M,记为$frac = f_{n-1}...f_{1}f_{0}$,是一个二进制小数,假定它有n位,那么表示的是$frac = \frac{frac}{2 ^ n}$,实际编码的时候会表示成另外的值,范围因为exponent变化,是$1 \sim 2 - \epsilon$或者是$0 \sim 1 - \epsilon$
- 阶码(exponent) E,记为$exp = e_{k-1}...e_{1}e_{0}$,编码的时候会有特判,假定它有k位
然后根据exp的值,浮点数可以分为以下3类(实际存在4类)并且有不同的编码
规格化的
exp != (0...000)_2 && exp != (1...111)_2,其余部分正常表达
最普遍的情况
这种情况下,阶码部分被解释为“偏置”(偏置值记为bias)形式表示的有符号整数,E = e - Bias,其中e是无符号整数,由exp表示,$bias = 2 ^ {k - 1} - 1$,由此可以得到$E$和$2 ^ E$的范围
此时尾数表示为$M = frac + 1$,$frac$在上面有写,写成小数形式就是$0.f_{n-1}...f_{1}f_{0} + 1 = 1.f_{n-1}...f_{1}f_{0}$
这种表达方式叫做“隐含的以1开头的”表示,然后我们总是可以通过调整阶码让尾数在M在范围$1 \leq M < 2$中,这种方法可以获得一个额外的精度为,因为第一位总是为1
非规格化的
exp == (0...000)_2,其余部分正常表达
此种情况下,$E = 1 - Bias$,$M = frac$
这种表示方法提供了两种功能
表达数值0,但是回顾整数用原码表示会产生两种0,由于符号位问题这里也是一样会产生两种0,但是有些时候可以等价看待,有时不能,例如
#include <iostream> using namespace std; int main(){ double a = 1.0 + 2.0; double b = 1.5 + 1.5; double c = 0.00000, d = -0.0000; cout << (a == b) << endl; cout << c << ' ' << d << endl; cout << (c == d) << endl; cout << (c > d) << endl; cout << (c < d) << endl; cout << (c >= d) << endl; cout << (c <= d) << endl; }
结果是
1
1
0
0
1
1
还有一个功能便是为了提供0附近的密集表达以产生一种“渐进下溢”(gradual underflow)的效果,可能出现的数值分布均匀地接近于0.下面会看到这个特性
特殊值
有时候会把特殊值认为特殊的非规格化值
无穷大
exp == (1.111)_2 && frac == (0...000)_2
在cmath中定义为#define INFINITY __builtin_inf()
没有包含cmath会导致无法使用,同时有些库如果间接include了这玩意然后代码中define了的话可能导致报错
返回INFINITY的情况就是浮点算数溢出
NaN
exp == (1.111)_2 && frac != (0...000)_2
在cmath中定义为#define NAN __builtin_nan("")
没有包含cmath会导致无法使用,同时有些库如果间接include了这玩意然后代码中define了的话可能导致报错
返回NAN的运算有以下三种
- 至少有一个参数是NaN的运算
- 不定式
- 下列除法运算:0/0、INFINITY/INFINITY、INFINITY/−INFINITY、−INFINITY/INFINITY、−INFINITY/−INFINITY
- 下列乘法运算:0×INFINITY、0×−INFINITY
- 下列加法运算:INFINITY + (−INFINITY)、(−INFINITY) + INFINITY
- 下列减法运算:INFINITY - INFINITY、(−INFINITY) - (−INFINITY)
- 产生复数结果的实数运算。例如:
- 对负数进行开偶次方的运算
- 对负数进行对数运算
- 对正弦或余弦到达域以外的数进行反正弦或反余弦运算
IEEE - 754 和 C++ 定义的一些具体的浮点数类型
注意以下针对的是IEEE的标准,但是并不是所有的C++编译器都会这么弄,但是至少OI中用的Gnu-Gcc和MinGW-Gcc是这样的
在C++ 98标准中,long double只要保证不比double精度少即可
在msvc中,long double定义为和double一样的精度
“半精度”浮点数
QAQ
float
double
long double
__float128
其实这个C++是有的,可以通过#include <quadmath.h>和在编译命令加上-lquadmath得到,有些版本不需要额外链接,有些版本不需要include
有一些题卡这个的精度那也就没办法,例如有一个51NOD 1836就要求精度1e-6 QWQ
在NOI Linux上好像可以直接食用
x86
0000000000000000000000000000000011111111111111111111111111111111
16
4
3218654224
3218654224
3218654224
3218654232
0000000000000000000000000000000000000000000000000000000000000000
0111111111111111000000000000000000000000000000000000000000000000
x64
0000000000000000000000000000000011111111111111111111111111111111
16
8
6487552
6487552
6487552
6487560
0000000000000000000000000000000000000000000000000000000000000000
0111111111111111000000000000000000000000000000000000000000000000
__float256

好像C++没有.jpg
总结和示例
假设现在有一个5为的浮点数,s = 0/1, k = 3, n = 2, bias = 3,那么可以观察到可以表达的数值分布


我们总结一下该图的特性
- 数值的绝对值从小到大分布为
0 -> 非规格化的值 -> 规格化的值 -> INF,然后还有NaN不计入内 - 规格化的值是不均匀的,越靠近原点越稠密,绝对值越大越稀疏
- 非规格化的值是均匀的
(第2点解释了上面废话中为什么模数不能太大
接着我们还可以看二进制上的分布

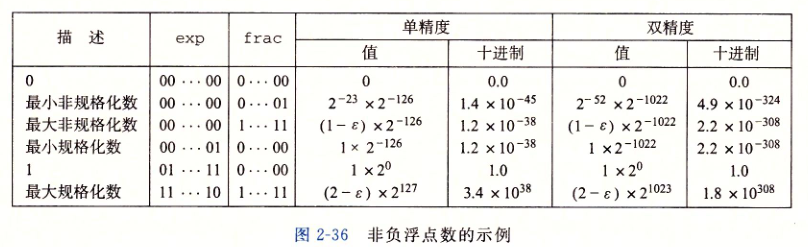


我们依然可以总结有一些特性
1. 最大非规格化的数和最小规格化的数平滑转换,界限分明,而且有确定的上界和下届
2. 如果把浮点数解释为无符号整数的二进制并且忽略正负值,那么二进制整数值越大,浮点数越大,所以排序的时候除了特判符号位其余的可以直接调用无符号整数排序
3. 0总是有一个所有位都是0的表示
4. 最小正非规格化的值$M = 2 ^ {-n}, E = - 2 ^ {k - 1} + 2,V = 2 ^ {- n - 2 ^ {k - 1} + 2}$
5. 最大非规格化的值$M = 1 - 2 ^ {-n}, E = E = - 2 ^ {k - 1} + 2, V = (1 - 2 ^ {-n}) * 2 ^ {- 2 ^ {k - 1} + 2}$
6. 最小的正规格化值$M = 1, E = - 2 ^ {k - 1} + 2, V = 2 ^ {- 2 ^ {k - 1} + 2}$
7. 1.0表示为$M = 1, E = 0$
8. 最大的规格化值$M = 2 - 2 ^ {-n}, E = 2 ^ {n - 1} - 1, V = (2 - 2 ^ {-n}) * 2 ^ {2 ^ {k - 1} - 1} = (1 - 2 ^ {- n - 1}) * 2 ^ {2 ^ {k - 1}}$
同时,一个整数转换为浮点数的时候有一下特性:
例如,这是数字233的转换:
#include <cmath> #include <iostream> using namespace std; union test{ struct{ unsigned long long ulx1; unsigned long long ulx2; }b; __float128 a; }; void print_bit64(unsigned long long tar){ for(int i = 63; ~i; i--){ putchar(bool((tar >> i) & 1) + 48); } puts(""); } int main(){ test t; t.a = 233; print_bit64(t.b.ulx2); t.b.ulx1 = 233; print_bit64(t.b.ulx1); return 0; }
0100000000000110110100100000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000011101001
稍微位移一下
iakioiak
0100000000000110110100100000000000000000000000000000000000000000
0000000000000000000000000000000000000000000000000000000011101001
发现整数的位数除了最高位的1在浮点数被隐藏了之外其余的相同,表现在尾码中
$M = \frac{4259306016766850789028922770063360}{2 ^ {112}} + 1 = 1.8203125, E = 2 ^ {16390 - 16384 + 1}, V = (2 ^ 7) * 1.8203125 = 233.0$
在浮点运算中,阶码可以衡量浮点数的最大值(除了INFINITY),尾数可以衡量浮点数的有效精度
关于精度的计算后面再说
浮点运算
舍入
IEEE有一些很奇怪的东西
| Mode / Example Value | +11.5 | +12.5 | −11.5 | −12.5 |
|---|---|---|---|---|
| to nearest, ties to even | +12.0 | +12.0 | −12.0 | −12.0 |
| to nearest, ties away from zero | +12.0 | +13.0 | −12.0 | −13.0 |
| toward 0 | +11.0 | +12.0 | −11.0 | −12.0 |
| toward +INFINITY | +12.0 | +13.0 | −11.0 | −12.0 |
| toward −INFINITY | +11.0 | +12.0 | −12.0 | −13.0 |
实际运算的时候,我们会有这种情况
有一个[11.0, 12.0]之间的数字,然后现在要求保留整数位
例如11.4,然后四舍五入到11,11.6四舍五入到12,但是关于11.5呢
根据浮点数的标准,应该对其“向偶舍入”,即取到12
为什么向偶舍入?考虑一个需要进行很多次的重复计算,如果每次对于所有的x.5都向上或向下的话,那么计算的值总是会偏上或偏下,而向偶舍入使得最终的期望值和整数值尽可能接近
以上说的是十进制下,十进制下看舍入结果看最后的一位,然后二进制下以1作为奇数位,0作为偶数位,需要做向偶舍入当且仅当有一个二进制小数abcd...efg.hijklm...opqr 100...000,其中r位于目标被舍入的位置,然后后面接着1000000...000,这种情况下,会倾向于是r = 0的舍入
我们对几个样例进行观察:
#include <cmath> #include <iostream> using namespace std; template <typename T> union test{ struct{ unsigned long long ulx1; unsigned long long ulx2; }b; T a; }; void print_bit64(unsigned long long tar){ for(int i = 63; ~i; i--){ putchar(bool((tar >> i) & 1) + 48); } puts(""); } int main(){ test<float> t1; test<double> t2; t2.a = 123.123123; print_bit64(t2.b.ulx1); t1.a = t2.a; print_bit64(t1.b.ulx1); return 0; }
得到的结果经过位数的处理对齐之后
0100000001011110110001111110000100111111010010101001100010101011
00001000010111101100011111100001010
iak
我们发现double转float之后按照向上舍入并且产生了进位
同样测试另外一个样本
把对t.a的操作换成t2.b.ulx1 = 4638364436225064960llu;
得到
0100000001011110110001111110000100110000000000000000000000000000
00001000010111101100011111100001010
iak
所以稍作总结得到如下结论:
假设目标位是r,二进制值位v,r后面的所有二进制串表示为w。那么
- 当w > 10000...000时v ++,并且有可能产生进位
- 当w = 10000...000时会变成0,即如果原来v = 1,那么产生进位,如果v = 0,保持为0
- 当w < 10000...000时不变
比较
关于比较——永远不要相信浮点数
例子数不胜数QAQ
float a(1.0 / 3); double b(1.0 / 3); if(a == b) cout << 1 << endl; else cout << 0 << endl;
会返回0
以下提供几个可用的建议
- 浮点数比较存在的主要问题就是丢失的精度,所以计算的时候尽量统一精度,比较的时候需要把某一边例如1 / 3.0这样的值强行转换为double,因为默认运算用的是float
- 储存的时候避免过多的类型转换,特别是浮点类型压缩,声明的时候可以使用1.0D来声明一个double
- 写一个comp函数比较浮点,一般提供1e5或者1e6的误差
- 避免在运算中出现特别小的值或者特别大的值,因为他们可能会被吃掉
- 大忌就是浮点类型和int类型的转换,精度丢失不止一点点
The IA32, x86-64, and Itanium processors support an 80-bit "double extended" extended precision format with a 64-bit significand. The Intel 8087 math coprocessor was the first x86 device which supported floating point arithmetic in hardware. It was designed to support a 32-bit "single precision" format and a 64-bit "double precision" format for encoding and interchanging floating point numbers. The temporary real (extended) format was designed not to store data at higher precision as such, but rather primarily to allow for the computation of double results more reliably and accurately by minimising overflow and roundoff-errors in intermediate calculations: for example, many floating point algorithms (e.g. exponentiation) suffer from significant precision loss when computed using the most direct implementations. To mitigate such issues the internal registers in the 8087 were designed to hold intermediate results in an 80-bit "extended precision" format. The 8087 automatically converts numbers to this format when loading floating point registers from memory and also converts results back to the more conventional formats when storing the registers back into memory. To enable intermediate subexpression results to be saved in extended precision scratch variables and continued across programming language statements, and otherwise interrupted calculations to resume where they were interrupted, it provides instructions which transfer values between these internal registers and memory without performing any conversion, which therefore enables access to the extended format for calculations – also reviving the issue of the accuracy of functions of such numbers, but at a higher precision.
因为在运算过程中会将内存(或高速缓存)中的值加载到CPU浮点寄存器(80 bit扩展精度)中,然后再进入CPU浮点计算单元进行计算,计算结果写回浮点寄存器,然后写回内存(或高速缓存)。从内存到浮点寄存器,浮点数的精度会扩展,从浮点寄存器到内存,浮点数的精度会降低(精度扩展通常没问题,但如果精度降低了,很可能值会发生变化,出现截断),而浮点运算的结果由于下面还要使用所以暂时保存在浮点寄存器中留待下次使用(没有及时写回内存,这是一种优化策略),从而导致数据并不是内存中和内存中的数据比较而是浮点寄存器中的值和内存中的值进行比较,而无论内存中是float类型还是double类型,其精度和浮点寄存器精度都不相同,从而导致比较结果是不相等。
同时考虑如下程序
float a = 0.1; float b = 0.1; b = b + 1 - 1; if(a == b) cout << 1 << endl; else cout << 0 << endl;
最后gdb给的值:

就算使用double


就算运算过程的1使用double也是如此,原因很简单,因为0.1是无法准确表示的,而换成0.25就不会发生这种事情,解决方案就是使用comp比较
还有一个更神的例子就是NOIP 2017 普及组 T1 成绩 一开始的数据设计成后面4或者7个点卡精度,卡的方法C++默认的浮点表示的是float,然后此题的运算涉及到了0.1之类的,然后后面还要扩大数值,然后就会产生整数1的误差
找到他谷上@ Douglas 的帖子:
题目:Ans = A * 20% + B * 30% + C * 50%
Hack数据
Input = 60 90 80
std-Output = 79
bad-Output = 78
30 pts
#include<bits/stdc++.h> using namespace std; int main() { int a,b,c; int s; scanf("%d%d%d",&a,&b,&c); s=(int)(a*0.2+b*0.3+c*0.5);//第一次强制转化 printf("%.lf",(double)s);//第二、三次强制转化 }
60 pts
#include<bits/stdc++.h> using namespace std; int main() { int a,b,c; scanf("%d%d%d",&a,&b,&c); int x=a*0.2+b*0.3+c*0.5;//第一次强制转化 printf("%d",x); }
100 pts - 1
#include<bits/stdc++.h> using namespace std; int main() { double a,b,c; double s; scanf("%lf%lf%lf",&a,&b,&c); s=a*0.2+b*0.3+c*0.5; printf("%.lf",s);//double型精度满足要求 }
#include<bits/stdc++.h> using namespace std; int main() { int a,b,c; int s; scanf("%d%d%d",&a,&b,&c); s=a*20/100+b*30/100+c*50/100;//不涉及强制转化 printf("%d",s); }
关于NaN和INFINITY的比较
记得发生的一个惨案就是HNOI 2017 队长快跑 精度要求1e-8,原题对于比较器的设计是这样的:
输出文件仅包含一行一个小数,表示最短道路的长度。当你的答案和标准答案的相对误差不超过10^−8时( 即|a-o|/a≤10-8时, 其中 a 是标准答案, o 是输出)认为你的答案正确。
我们发现如果o = NAN的话,对于所有测试点都可以过,因为SPJ使用了差不多如下代码:
if(fabs(a - o) / a > 1e-8) puts("fake"); else puts("ojbk");
然后NAN和其他数除了$!=$以外的运算返回0
所以当时的高分代码
- 暴力中间对于负数开了根号,然后最后输出NAN
- 直接输出NAN
差不多总结就是:
- NAN和其他值的<,>,≤,≥,==<, >, \leq, \geq, ==<,>,≤,≥,==比较返回0,特例是直接用
NAN == NAN判断返回1 - 非特殊值和INFINITY的比较总是INFINITY大
- INFINITY被认为是相同的值
四则运算
加减法
如果不考虑舍入,那么实数的加法是满足阿贝尔群的,但是考虑浮点这种类型的舍入之后这个性质不再满足
浮点数加法满足交换律但不满足结合律,例如考虑
((float)3.14 + 1e10) - 1e10
和
(float)3.14 + (1e10 - 1e10)
前者答案为0,后者答案为3.14,因为前者的舍入把3.14吃掉了
因此,编译器对浮点加法运算一般都采取保守的态度,避免产生对结果的影响,例如
x = a + b + c
y = b + c + d
不会被优化成
t = a + b
x = t + c
y = t + d
大多数值在浮点加法下都有逆元,除了NAN和INFINITY比较特殊,可以参考上面写了的运算
浮点加法满足单调性,即如果$a \geq b$,则$x + a \geq x + b$,即使考虑溢出依然满足,但是无符号或者是补码加法不满足这个性质,因为溢出可能导致结果不单调
乘除法
满足交换律
不满足结合律,因为INFINITY问题
不满足分配律,因为INFINITY和NAN问题
满足单调性
这些结果体现在OI中就是会发现浮点运算特别慢,即使CPU计算浮点数有一个理论的时钟周期,但是实际上看到的结果会慢的多,因为对浮点不会做优化,这些优化一般需要手动做
数值转换
- int转float不会溢出但是可能会出现舍入
- int或者float转double由于double的数值范围和精度更大,所以一定能保留精确值(相对于double,例如0.1本身就无法精确表示)
- double转float可能会出现溢出或者舍入
- float或double转int,值向0舍入,而且可能会溢出,而且这个溢出结果C语言标准没有定义,例如以Inter兼容的微处理器指定位模式[10...00]为整数不确定值,即TMinwTMin_wTMinw(当前类型最小值)。那么当一个浮点到整数的转换当找不到一个合适的近似值的时候就会产生这样一个值。例如部分电脑上(int)+1e10返回-21483648,本机x64下返回2147483647,x86返回2147483647
示例
运算的示例
假设f和d是float和double,且不是特殊值,假设x是int
- x == (int)(double)x -> 1
- x == (int)(float)x -> 0, 当x = Tmax(int)右式等于-2147483648,因为右式转float之后的值为


- d == (double)(float)d -> 0,当d = 1e40时右式得到INFINITY
- f == (float)(double)f -> 1,因为这样不会出现精度损失
- f == -(-f) -> 1,因为运算只对s产生影响
- 1.0 / 2 == 1 / 2.0 -> 1,因为执行浮点除法之前两边都会完成类型转换
- d * d >= 0.0 -> 1,即使溢出表达式成立
- (f + d) - f == d -> 0,会产生舍入问题
其他的东西
有效精度
其他的其他
如果你认真读了上面的话,那么就没有什么东西了
当然还有一个有意思的事情就是使用无符号整数+特殊处理的排序可以排出一个非常优美的序:
-inf -inf -234.000000 -234.000000 -123.000000 -123.000000 -0.100000 -0.100000 -0.000000 -0.000000 nan nan 0.000000 0.000000 0.100000 0.100000 123.000000 123.000000 234.000000 234.000000 inf inf
也就是nan和inf都有其安排
如果用sort或者stable_sort这种辣鸡玩意就是这种不优美的东西
nan -inf -234.000000 -123.000000 -0.100000 0.000000
-0.000000 0.100000 123.000000 234.000000 inf nan -inf -234.000000 -123.000000 -0.100000 0.000000 -0.000000 0.100000 123.000000 234.000000 inf
浮点数基数排序
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; // Source Code /* * 食用说明 * 前面针对bit的排序除了80Bit的其他的返回的都是a为sorted数组 * 后面long double的排序也是交换了一次数组,还有一个不交换的版本 * 传进去的参数都是1. 排序范围, 2. 待排序数组, 3. 中间值数组,待排序数组要求数据下标从1开始 * 建议把那个通用的Radix_Sort_Bit函数内变换循环顺序后进行循环展开 * Radix_Sort_Bit排序只适合于小端法机器 */ template <typename T> inline void Radix_Sort_32Bit(register const int n, T *a, T *b){ unsigned r1[0x100], r2[0x100], r3[0x100], r4[0x100]; memset(r1, 0, sizeof(r1)), memset(r2, 0, sizeof(r2)); memset(r3, 0, sizeof(r3)), memset(r4, 0, sizeof(r4)); register int i; register unsigned int tmp_int; register T * j, *tar; for(j = a + 1, tar = a + 1 + n; j != tar; ++j){ tmp_int = * (unsigned int *) j; ++r1[tmp_int & 0xff]; ++r2[(tmp_int >> 0x8) & 0xff]; ++r3[(tmp_int >> 0x10) & 0xff]; ++r4[tmp_int >> 0x18]; } for(i = 1; i <= 0xff; ++i){ r1[i] += r1[i - 1]; r2[i] += r2[i - 1]; r3[i] += r3[i - 1]; r4[i] += r4[i - 1]; } for(j = a + n; j != a; --j){ tmp_int = * (unsigned int *) j; b[r1[tmp_int & 0xff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (unsigned int *) j; a[r2[(tmp_int >> 0x8) & 0xff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (unsigned int *) j; b[r3[(tmp_int >> 0x10) & 0xff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (unsigned int *) j; a[r4[tmp_int >> 0x18]--] = *j; } } template <typename T> inline void Radix_Sort_64Bit(register const int n, T *a, T *b){ unsigned r1[0x10000], r2[0x10000], r3[0x10000], r4[0x10000]; memset(r1, 0, sizeof(r1)), memset(r2, 0, sizeof(r2)); memset(r3, 0, sizeof(r3)), memset(r4, 0, sizeof(r4)); register int i; register unsigned long long tmp_int; register T * j, *tar; for(j = a + 1, tar = a + 1 + n; j != tar; ++j){ tmp_int = * (unsigned long long *) j; ++r1[tmp_int & 0xffff]; ++r2[(tmp_int >> 0x10) & 0xffff]; ++r3[(tmp_int >> 0x20) & 0xffff]; ++r4[tmp_int >> 0x30]; } for(i = 1; i <= 0xffff; ++i){ r1[i] += r1[i - 1]; r2[i] += r2[i - 1]; r3[i] += r3[i - 1]; r4[i] += r4[i - 1]; } for(j = a + n; j != a; --j){ tmp_int = * (unsigned long long *) j; b[r1[tmp_int & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (unsigned long long *) j; a[r2[(tmp_int >> 0x10) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (unsigned long long *) j; b[r3[(tmp_int >> 0x20) & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (unsigned long long *) j; a[r4[tmp_int >> 0x30]--] = *j; } } template <typename T> inline void Radix_Sort_128Bit(register const int n, T *a, T *b){ unsigned r1[0x10000], r2[0x10000], r3[0x10000], r4[0x10000]; unsigned r5[0x10000], r6[0x10000], r7[0x10000], r8[0x10000]; memset(r1, 0, sizeof(r1)), memset(r2, 0, sizeof(r2)); memset(r3, 0, sizeof(r3)), memset(r4, 0, sizeof(r4)); memset(r5, 0, sizeof(r5)), memset(r6, 0, sizeof(r6)); memset(r7, 0, sizeof(r7)), memset(r8, 0, sizeof(r8)); register int i; register __uint128_t tmp_int; register T * j, *tar; for(j = a + 1, tar = a + 1 + n; j != tar; ++j){ tmp_int = * (__uint128_t *) j; ++r1[tmp_int & 0xffff]; ++r2[(tmp_int >> 0x10) & 0xffff]; ++r3[(tmp_int >> 0x20) & 0xffff]; ++r4[(tmp_int >> 0x30) & 0xffff]; ++r5[(tmp_int >> 0x40) & 0xffff]; ++r6[(tmp_int >> 0x50) & 0xffff]; ++r7[(tmp_int >> 0x60) & 0xffff]; ++r8[tmp_int >> 0x70]; } for(i = 1; i <= 0xffff; ++i){ r1[i] += r1[i - 1]; r2[i] += r2[i - 1]; r3[i] += r3[i - 1]; r4[i] += r4[i - 1]; r5[i] += r5[i - 1]; r6[i] += r6[i - 1]; r7[i] += r7[i - 1]; r8[i] += r8[i - 1]; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r1[tmp_int & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r2[(tmp_int >> 0x10) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r3[(tmp_int >> 0x20) & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r4[(tmp_int >> 0x30) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r5[(tmp_int >> 0x40) & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r6[(tmp_int >> 0x50) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r7[(tmp_int >> 0x60) & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r8[tmp_int >> 0x70]--] = *j; } } template <typename T> inline void Radix_Sort_80Bit(register const int n, T *a, T *b){ unsigned r1[0x10000], r2[0x10000], r3[0x10000], r4[0x10000], r5[0x10000]; memset(r1, 0, sizeof(r1)), memset(r2, 0, sizeof(r2)); memset(r3, 0, sizeof(r3)), memset(r4, 0, sizeof(r4)); memset(r5, 0, sizeof(r5)); register int i; register __uint128_t tmp_int; register T * j, *tar; for(j = a + 1, tar = a + 1 + n; j != tar; ++j){ tmp_int = * (__uint128_t *) j; ++r1[tmp_int & 0xffff]; ++r2[(tmp_int >> 0x10) & 0xffff]; ++r3[(tmp_int >> 0x20) & 0xffff]; ++r4[(tmp_int >> 0x30) & 0xffff]; ++r5[tmp_int >> 0x40]; } for(i = 1; i <= 0xffff; ++i){ r1[i] += r1[i - 1]; r2[i] += r2[i - 1]; r3[i] += r3[i - 1]; r4[i] += r4[i - 1]; r5[i] += r5[i - 1]; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r1[tmp_int & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r2[(tmp_int >> 0x10) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r3[(tmp_int >> 0x20) & 0xffff]--] = *j; } for(j = b + n; j != b; --j){ tmp_int = * (__uint128_t *) j; a[r4[(tmp_int >> 0x30) & 0xffff]--] = *j; } for(j = a + n; j != a; --j){ tmp_int = * (__uint128_t *) j; b[r5[(tmp_int >> 0x40) & 0xffff]--] = *j; } } template <typename T> inline void Radix_Sort_Bit(register const int n, T *a, T *b){ size_t size_of_type = sizeof(a); size_t num_of_buc = ((size_of_type >> 1) + 1) >> 1; unsigned r[num_of_buc][0x10000]; memset(r, 0, sizeof(r)); register int i, k; register unsigned short tmp_us; register T * j, *tar; for(k = 0; k < num_of_buc; ++k){ for(j = a + 1, tar = a + 1 + n; j != tar; ++ j){ tmp_us = * (((unsigned short *)j) + k); ++ r[k][tmp_us]; } } for(k = 0; k < num_of_buc; k++) for(i = 1; i <= 0xffff; i++) r[k][i] += r[k][i - 1]; for(k = 0; k < num_of_buc; k += 0x2){ i = k; for(j = a + n; j != a; --j){ tmp_us = * (((unsigned short *)j) + i); b[r[i][tmp_us]--] = *j; } i |= 1; for(j = b + n; j != b; --j){ tmp_us = * (((unsigned short *)j) + i); a[r[i][tmp_us]--] = *j; } } } inline void Radix_Sort_Float(register const int n, float *a, float *b){ Radix_Sort_32Bit(n, a, b); reverse(a + 1, a + 1 + n); reverse(upper_bound(a + 1, a + 1 + n, float(-0.0)), a + 1 + n); } inline void Radix_Sort_Double(register const int n, double *a, double *b){ Radix_Sort_64Bit(n, a, b); reverse(a + 1, a + 1 + n); reverse(upper_bound(a + 1, a + 1 + n, double(-0.0)), a + 1 + n); } inline void Radix_Sort_LDouble(register const int n, long double *a, long double *b){ Radix_Sort_80Bit(n, a, b); reverse(b + 1, b + 1 + n); reverse(upper_bound(b + 1, b + 1 + n, (long double)(-0.0)), b + 1 + n); swap(a, b); } inline void Radix_Sort_LDouble_B(register const int n, long double *a, long double *b){ Radix_Sort_80Bit(n, a, b); reverse(b + 1, b + 1 + n); reverse(upper_bound(b + 1, b + 1 + n, (long double)(-0.0)), b + 1 + n); } double a[100], b[100]; int main(){ int n; scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%lf", a + i); Radix_Sort_Double(n, a, b); for(int i = 1; i <= n; i++) printf("%lf ", a[i]); return 0; }


