容斥原理学习笔记
基本容斥
记住这两个定理即可
二项式反演
首先得晓得两个很基本的式子
\[\begin{align*}
若g_n&=\sum_{i=0}^n C(n,i)*f_i
\\
则f_n&=\sum_{i=0}^n (-1)^{n-i}*C(n,i)*g_i
\end{align*}
\]
\[\begin{align*}
若g_n&=\sum_{i\ge n} C(i,n)*f_i
\\
则f_n&=\sum_{i\ge n} (-1)^{i-n}*C(i,n)*g_i
\end{align*}
\]
然后有些题经常会让你求\(N\)个物品，恰好有\(k\)个物品特殊的方案数\(f_k\),且对于\(k=0...n\)都输出答案。
这种时候我们考虑去求至少有\(k\)个物品特殊的方案数\(g_k\)，或者至多有\(k\)个位置特殊的方案数\(h_k\)。
如果求了\(g_k\)
那么则有
\[\begin{align*}
&f_n=g_n-\sum_{i\ge n+1} C(i,n)*f_i
\\
即 &g_n=\sum_{i\ge n} C(i,n)*f_i
\\
所以 &f_n=\sum_{i\ge n} (-1)^{i-n}*C(i,n)*g_i
\end{align*}
\]
减法卷积即可
如果求了\(h_k\)
那么则有
\[\begin{align*}
&h_n=\sum_{i=0}^n C(n,i)*f_i
\\
所以 &f_n=\sum_{i=0}^n (-1)^{n-i}*C(n,i)*h_i
\end{align*}
\]
卷积即可
斯特林容斥
反演的本质是：我们想计算\(f_n\)，但不会算。
但我们可以轻松的计算出\(\sum_{i\ge n}w[i][n]*f_i\)
然后我们可以根据\(w\)函数的一些性质来计算\(f\)
如果我们取\(w\)函数为第二类斯特利林数
那么
考虑以下定理
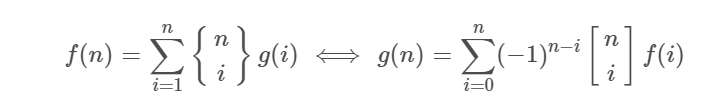
直接应用该式即可。
