生成函数学习笔记
一般生成函数 OGF
A是一类组合对象构成的集合
其中大小为i的物品数量为A_i
\[A(x)=\sum_{n>=0}A_n*x^n
\]
组成序列
组合元素可以理解为一种由基本元素构成的集合
\[\\
\\
\\
\]


\[\\
\\
\\
\]
这里所说的SEQ(A)是一个以OGF为自变量的函数
表示的是有A中元素有序排列,大小相加构成的所有元素 所组成的集合
结合上文的两个例子理解
\(f(x)\)存在逆元的充要条件是\(f(x)\)的常数项存在逆元
指数生成函数 EGF
A是一类组合对象构成的集合
其中大小为i的物品数量为A_i
\[A(x)=\sum_{n>=0}\frac{A_n}{n!}*x^n
\]
EGF的乘法定义
\[\begin{align*}
&设C(x)=A(X)*B(X)
\\
&则系数C_n=\sum_{i+j=n}A_i*B_j*\frac{(i+j)!}{i!*j!}
\\
&等价于\frac{C_n}{n!}=\sum_{i+j=n}\frac{A_i}{i!}*\frac{B_j}{j!}
\\
\end{align*}
\]
实际做题中
对于EGF,我们通常把它变成OGF
按照OFG的运算准则进行运算
然后最后再重新变换为EGF
OGF转EGF 系数除以\(n!\)
EGF转OGF 系数乘以\(n!\)
组成序列/集合
\[\\
\\
\\
\]
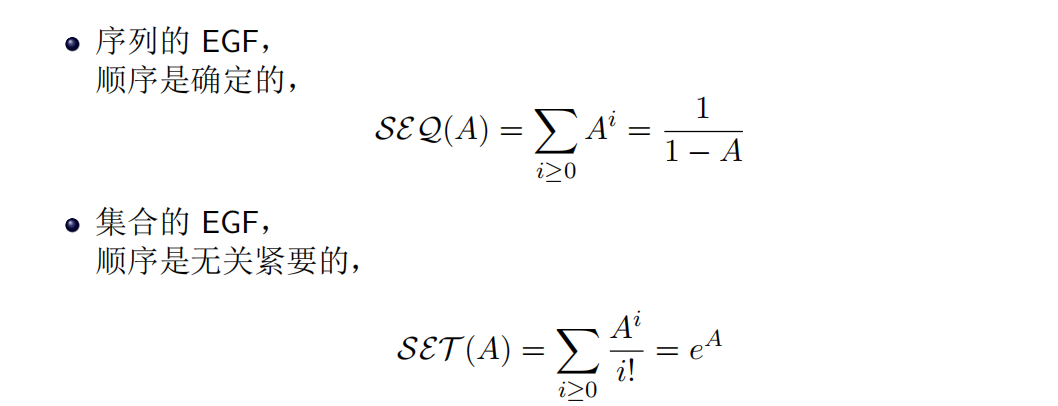


 浙公网安备 33010602011771号
浙公网安备 33010602011771号