P3911 最小公倍数之和
终于找到了一个只会用[gcd(i,j)==1] = sigema d|gcd(i,j) mu(d) 做不了的题。
考虑枚举gcd后。
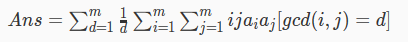
此时,ans可以表示为一个 sigema x f(x)的形式。
考虑对反演f(x)。

然后发现f(x)也很容易在nlogn的复杂度内算出来,就做完了。
#include<bits/stdc++.h>
#define N 110000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline ll read()
{
char ch=0;
ll x=0,flag=1;
while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
return x*flag;
}
bool is_prime[N];
ll a[N],f[N],mu[N],prime[N];
void solve(ll n)
{
memset(is_prime,true,sizeof(is_prime));
is_prime[0]=is_prime[1]=false;mu[0]=mu[1]=1;
for(ll i=2,cnt=0;i<=n;i++)
{
if(is_prime[i])prime[++cnt]=i,mu[i]=-1;
for(ll j=1;j<=cnt;j++)
{
if(i*prime[j]>n)break;
is_prime[i*prime[j]]=false;
if(i%prime[j])mu[i*prime[j]]=-mu[i];
else{mu[i*prime[j]]=0;break;}
}
}
}
int main()
{
ll n=read(),len=5e4;solve(len);
for(ll i=1;i<=n;i++)a[read()]++;
for(ll i=1;i<=len;i++)
{
for(ll j=i;j<=len;j+=i)f[i]+=a[j]*j;
f[i]*=f[i];
}
ll ans=0;
for(ll i=1;i<=len;i++)
{
ll tot=0;
for(ll j=i;j<=len;j+=i)tot+=mu[j/i]*f[j];
ans+=tot/i;
}
printf("%lld",ans);
return 0;
}


