P3312 [SDOI2014]数表

https://www.luogu.org/problemnew/show/P3312

比较nb的一个题。

首先考虑没有a的限制怎么搞。

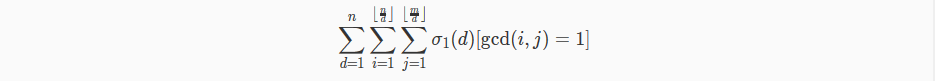
把d提到前面

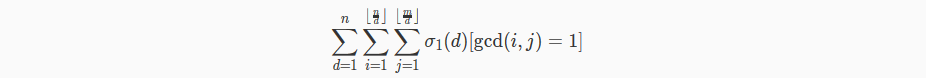
mobius反演一下

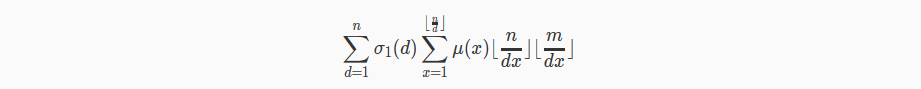
令T=dx,把T挪到前面（没想到这一步！）

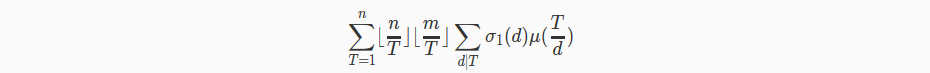
设F(x)=d(x)和mu(x)的狄利克雷卷积。

然后考虑怎么带上a的限制，只要能动态维护F(x)即可sqrt(n)*O(维护复杂度)解决本题。

考虑把询问离线，并把d(x)按照权值排序，逐一加入，加入第i项后，它会对F(x)中为i的倍数的项产生一个d(i)✖mu(x/i)的贡献。

有发现除法分块求答案时，需要用到F(x)的区间和。

因此用树状数组维护一下即可。

#include<bits/stdc++.h>
#define N 220000
#define L 200000
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline int read()
{
	char ch=0;
	int x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
bool is_prime[N];
int c[N],p[N],d[N],mu[N],prime[N];
void solve(int n)
{
	memset(is_prime,true,sizeof(is_prime));
	is_prime[0]=is_prime[1]=false;
	c[0]=c[1]=p[0]=p[1]=d[0]=d[1]=mu[0]=mu[1]=1;
	for(int i=2,cnt=0;i<=n;i++)
	{
		if(is_prime[i])c[i]=p[i]=i,prime[++cnt]=i;
		for(int j=1;j<=i;j++)
		{
			int t=i*prime[j];
			if(t>n)break;
			is_prime[t]=false;
			if(i%prime[j])c[t]=p[t]=prime[j];
			else c[t]=prime[j],p[t]=p[i]*prime[j];
			if(i%prime[j]==0)break;
		}
	}
	for(int i=2;i<=n;i++)
	if(i==p[i])
	{
		if(is_prime[i])d[i]=1+i,mu[i]=-1;
		else d[i]=d[i/c[i]]+i,mu[i]=0;
	}
	else
	{
		int j=p[i];
		d[i]=d[j]*d[i/j];
		mu[i]=mu[j]*mu[i/j];
	}
}
struct node{int x,id;}f[N];
bool cmp_node(node a,node b){return a.x<b.x;}
struct query{int n,m,k,id;}q[N];
bool cmp_query(query a,query b){return a.k<b.k;}
int t,cnt,len,s[N],ans[N];
void add(int x,int k){for(;x<=len;x+=((+x)&(-x)))s[x]+=k;}
int get(int l,int r)
{
	int x,ans=0;
	for(x=l-1;x;x-=((+x)&(-x)))ans-=s[x];
	for(x=r+0;x;x-=((+x)&(-x)))ans+=s[x];
	return ans;
}
int main()
{
	t=read();len=1e5;solve(len);
	for(int i=1;i<=len;i++)f[i]={d[i],i};sort(f+1,f+len+1,cmp_node);
	for(int i=1;i<=t;i++)
	{
		int n=read(),m=read(),x=read();
		if(x>=0)q[++cnt]={n,m,x,i};
	}
	sort(q+1,q+t+1,cmp_query);
	for(int i=1,j=0;i<=cnt;i++)
	{
		while(j!=len&&f[j+1].x<=q[i].k)
		{
			j++;
			for(int k=f[j].id;k<=len;k+=f[j].id)add(k,f[j].x*mu[k/f[j].id]);
		}
		int n=q[i].n,m=q[i].m; 
		for(int l=1,r;l<=min(n,m);l=r+1)
		{
			r=min(n/(n/l),m/(m/l));			
			ans[q[i].id]+=(n/l)*(m/l)*get(l,r);
		}		
	}
	
	for(int i=1;i<=t;i++)
	{
		ll x=ans[i],p=1ll<<31;
		printf("%lld\n",(x%p+p)%p);
	}
	return 0;
}