凸集的开、闭、紧

更新于20181220.01:13之前的定义有疏漏，特别是对开凸集的定义是错误的臆想，举出的一个例子半开半闭。

对于开集，开集，是拓扑学里最基本的概念之一。设A是度量空间X的一个子集。如果A中的每一个点都有一个以该点为球心的小球包含于A，则称A是度量空间X中的一个开集。

在拓扑空间中，闭集是指其补集为开集的集合。 由此可以引申在度量空间中，如果一个集合所有的极限点都是这个集合中的点，那么这个集合是闭集。不要混淆于闭流形。

?题目

有理数集在R上的欧氏拓扑下既不是开集也不是闭集？

优质解答

开集的定义是集合A中的每一个点都是内点,对于有理数集Q,任取Q中一点r,由于有理数和无理数在R上都是稠密的,所以不可能找到r的一个邻域(a,b),使得在(a,b)内的任意点都属于Q（就是说一个有理数的任何邻域内都存在无理数）,r不是内点,所以Q不是开集.对于闭集,通常有不同的定义,一个等价的定义是,集合A满足条件A‘包含于A,这里A’表示A的所有极限点构成的集合,称为A的导集,来看有理数集Q,从Q中取一系列数r1,r2...rn,这个有理数序列{rn}的极限不一定是有理数（事实上我们就是借助有理数序列来定义无理数的）,例如有理数序列1,1,4,1.41,1.414...的极限是无理数√2,因此Q‘是不可能包含于Q的.所以Q也不是闭集.有不明白的地方欢迎追问.

分割线

～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～～

凸集类型  |  比较条件	条件A 任何的“存在极限的”“C包含的元素的序列“的”极限点”属于C	条件B C是否有完全包围的边界（就是无限的）
开	不满足任何	可能有部分边界，可能没有边界
闭	满足任何	一定有部分边界，不一定完全边界
紧	满足任何	一定有完全边界

 

开凸集分为：

1. 部分满足A,   完全不满足A

2.部分满足B，完全不满足B

组合有4种

类似的，闭，紧；

举例：

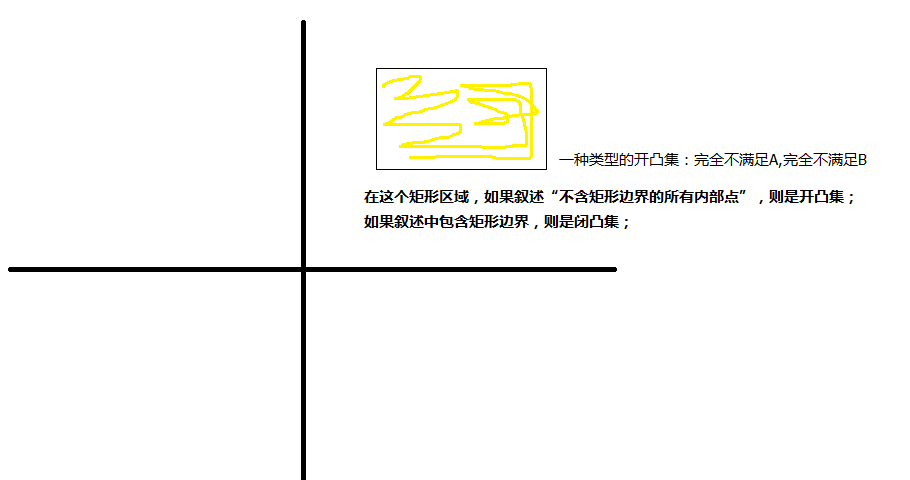
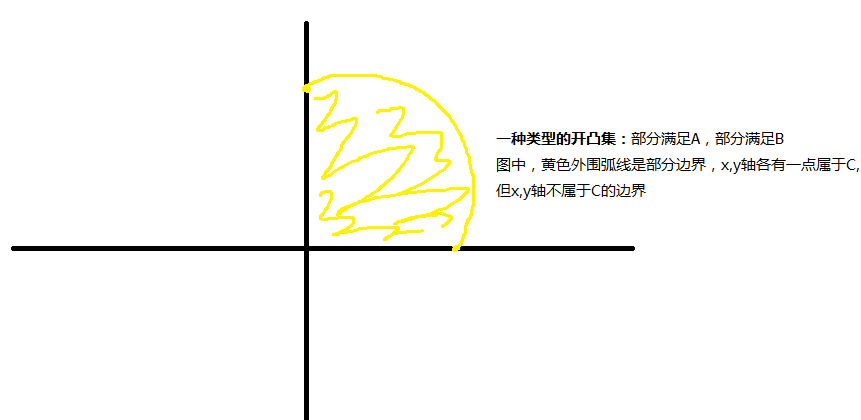
参考：stackexchange

 

 

 

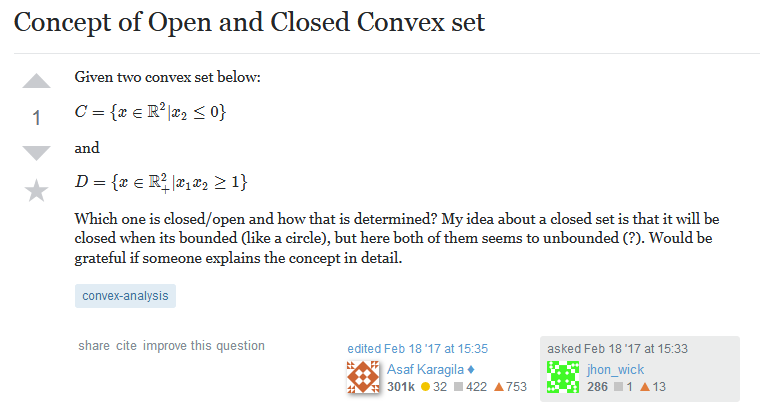
举例：