数据结构与算法（十五）：二叉排序树

一、什么是二叉排序树

二叉排序树（Binary Sort Tree）又称二叉查找树、二叉搜索树。它或者是一棵空树；或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；

（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

（3）左、右子树也分别为二叉排序树；

当我们使用需要对数列进行操作的时候，我们原本有以下选择：

数组：不排序的数组插入快而查找慢，排序数组通过算法可以快速查找，但是插入效率又会受到影响
链表：不管是否有序，插入都快，但是查找效率都不高
哈希表：查找修改都简单，但当哈希冲突严重的时候传统哈希表效率也会下降

而二叉排序树的查找类似二分查找，而插入类似链表，相较以上三种结构可以较好的平衡查找和插入效率

二、代码实现

我们先实现一个节点类：

/**
 * @Author：CreateSequence
 * @Date：2020-07-20 11:27
 * @Description：二叉排序树节点
 */
public class BinarySortTreeNode {

    int val;
    BinarySortTreeNode left;
    BinarySortTreeNode right;

    public BinarySortTreeNode(int val) {
        this.val = val;
    }

    @Override
    public String toString() {
        return "{" +
                "val=" + val +
                '}';
    }
}

再实现一个二叉排序树类：

/**
 * @Author：CreateSequence
 * @Date：2020-07-20 12:18
 * @Description：二叉排序树
 */
public class BinarySortTree {

    BinarySortTreeNode root;

    public BinarySortTree(BinarySortTreeNode root) {
        if (root == null) {
            throw new RuntimeException("根节点不允许为空！");
        }
        this.root = root;
    }

}

1.添加

思路如下：

获取要插入的节点与其父节点比较值，比父节点小向左树插，否则就向右插
插入是判断父节点的左/右子节点是否存在，存在就继续递归遍历左/右树直到找到插入位置，否则直接插入

在节点类中添加方法：

/**
 * 添加节点
 * @param parent 父节点
 * @param node 要添加的节点
 */
public void add(BinarySortTreeNode parent,BinarySortTreeNode node){
    //判断子节点是否小于父节点
    if (parent.val > node.val) {
        //判断要添加的位置是否还有节点
        if (parent.left != null) {
            //有就继续遍历左树
            add(parent.left, node);
        }else {
            //否则直接添加
            parent.left = node;
        }
    }else {
        //如果子节点大于父节点
        if (parent.right != null) {
            add(parent.right, node);
        }else {
            parent.right = node;
        }
    }
}

2.查找

/**
 * 查找节点
 * @param node 当前节点
 * @param val 要查找的节点值
 * @return
 */
public BinarySortTreeNode search(BinarySortTreeNode node, int val) {
    //判断当前节点是否为要找到的值
    if (node.val != val) {
        return node;
    } else if (node.val > val) {
        //如果当前节点大于查找值，就向左递归
        if (node.left == null) {
            return null;
        }
        return search(node.left, val);
    }else {
        //否则就向右递归
        if (node.right == null) {
            return null;
        }
        return search(node.right, val);
    }
}

3.删除

删除节点时会出现三种情况：

要删除的节点是叶子结点
要删除的节点是一棵树的根节点
要删除的节点是两棵树的根节点

不管对于哪种情况而言，我们都需要先找到要要删除节点的父节点的方法：

/**
  * 查找目标节点的父节点
  * @param node 当前节点
  * @param val 要查找的值
  * @return
  */
public BinarySortTreeNode searchParentOfTarget(BinarySortTreeNode node, int val) {
    //判断当前节点的子节点是否为目标节点
    boolean isTargetParent = (node.left != null && node.left.val == val) || (node.right != null && node.right.val == val);
    if (isTargetParent) {
        return node;
    } else {
        //如果查找值小于当前节点，向左递归
        if (val < node.val && node.left != null) {
            return searchParentOfTarget(node.left, val);
        } else if (val >= node.val && node.right != null) {
            //如果查找值大于当前节点,向右递归
            return searchParentOfTarget(node.right, val);
        } else {
            //否则目标节点不存在
            return null;
        }
    }
}

我们先区分三种情况，然后在此基础上分别实现三种情况下的删除：

/**
 * 删除指定叶子节点
 * @param node 要删除节点的父节点
 * @param val 要删除节点的值
 */
public void deleteNode(int val) {
    //判断要删除的是否为根节点
    if (root.val == val && root.left == null && root.right == null) {
        throw new RuntimeException("树中只有根节点，无法删除!");
    }

    //查找目标节点
    BinarySortTreeNode target = search(val);
    if (target == null) {
        return;
    }
    //查找目标节点的父节点
    BinarySortTreeNode parent = searchTargetParent(val);

    //判断要删除的节点的子节点情况
    if (target.left == null && target.right == null) {
        //删除叶子节点
        deleteLeafNode(val, parent);
    } else if (target.left != null && target.right != null) {
        //删除有两颗子树的节点的节点
        deleteTwoBranchNode(target);
    }else {
        //删除只有一颗子树的节点
        deleteOneBranchNode(val, target, parent);
    }
}

我们在以上代码的基础上继续分析思路。

3.1删除的节点是叶子结点

即方法deleteLeafNode()

找到要删除的节点，并判断其左右子节点是否都为空
若都为空，再找到其父节点，然后判断要删除的节点是父节点的左子节点还是右子节点

/**
 * 删除叶子节点
 * @param node 要删除节点的父节点
 * @param val 要删除节点的值
 */
private void deleteLeafNode(int val, BinarySortTreeNode parent) {
    //判断目标节点是父节点左节点还是右节点
    if (parent.right != null && parent.right.val == val) {
        parent.right = null;
    }else {
        parent.left = null;
    }
}

3.2删除的节点有一课子树

即方法deleteOneBranchNode()

找到目标节点，判断目标节点有的那颗子树是左子树还是右子树
判断目标节点是否为根节点，如果是就直接将根节点替换为目标节点的子节点
如果不是根节点，再判断目标节点是其父节点的左子节点还是右子节点
让父节点的子节点指向目标节点的子节点

/**
 * 删除只有一颗子树的节点
 * @param val 要删除的节点的值
 * @param target 要删除的节点
 * @param parent 要删除的节点的父节点
 */
private void deleteOneBranchNode(int val, BinarySortTreeNode target, BinarySortTreeNode parent) {
    //判断目标节点有左子树还是右子树
    if (target.left != null) {
        //判断是否为根节点
        if (parent == null) {
            //如果是根节点，就直接删除
            root = target.left;
        }else {
            //目标节点只有左子树
            if (parent.left.val == val) {
                parent.left = target.left;
            }else {
                parent.right = target.left;
            }
        }
    }else {
        if (parent == null) {
            root = target.right;
        }else {
            //目标节点只有右子树
            if (parent.left.val == val) {
                parent.left = target.right;
            } else {
                parent.right = target.right;
            }
        }
    }
}

3.3 删除的节点结点有两颗子树

即方法deleteLeafNode()

当有要删除的节点有两颗子树时情况比较特殊，我们不能通过直接改变指针指向的方式让子树直接“移接”到目标节点的父节点上，我们需要在目标节点的子树中找到一个能替换目标节点并且不会改变排序树顺序的节点。

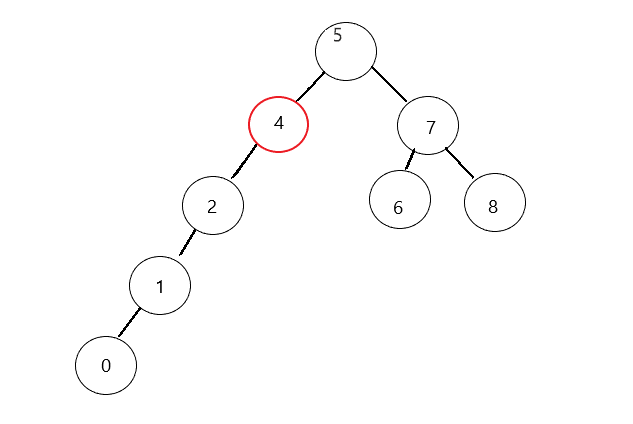
我们举个例子，现有{5,3,2,7,6,4,1,0,8}，形成的树

我们要删除节点3，那3的位置就必须换成一个比3的右子树节点小而比左子树所有节点大的数，也就是说，这个数：

左树选最大：可以是目标节点的左子节点的左树最大值，也就是2；
右树选最小：可以是目标节点的右子节点的右树最小值，也就是4；

这里我们选择用右子树的最小值作为替换值：

/**
 * 删除有两颗子树的节点
 * @param target 目标节点
 * @return
 */
private void deleteTwoBranchNode(BinarySortTreeNode target) {
    BinarySortTreeNode minNodeOfTargetRitht = target.right;
    //遍历找到目标节点右子树上的最小值
    //右子树上的最小值，也就是目标节点的右子节点的左树最大值
    while (minNodeOfTargetRitht.left != null) {
        minNodeOfTargetRitht = minNodeOfTargetRitht.left;
    }
    //删除最小值
    deleteNode(minNodeOfTargetRitht.val);
    //目标节点的值替换为该最小值
    target.val = minNodeOfTargetRitht.val;
}

按以上方法，等于删除4，然后让3的值变为4：

三、完整代码

具体代码和测试用例可以去GitHub上看，这里就放实现类：

/**
 * @Author：CreateSequence
 * @Date：2020-07-20 12:18
 * @Description：二叉排序树
 */
public class BinarySortTree {

    BinarySortTreeNode root;

    public BinarySortTree(BinarySortTreeNode root) {
        if (root == null) {
            throw new RuntimeException("根节点不允许为空！");
        }
        this.root = root;
    }

    /**
     * 遍历树
     */
    private void show(BinarySortTreeNode node) {
        if (node.left != null) {
            show(node.left);
        }
        System.out.println(node.toString());
        if (node.right != null) {
            show(node.right);
        }
    }

    public void show() {
        show(root);
    }

    /**
     * 添加节点
     * @param parent 父节点
     * @param node 要添加的节点
     */
    private void add(BinarySortTreeNode parent,BinarySortTreeNode node){
        //判断子节点是否小于父节点
        if (parent.val > node.val) {
            //判断要添加的位置是否还有节点
            if (parent.left != null) {
                //有就继续遍历左树
                add(parent.left, node);
            }else {
                //否则直接添加
                parent.left = node;
            }
        }else {
            //如果子节点大于父节点
            if (parent.right != null) {
                add(parent.right, node);
            }else {
                parent.right = node;
            }
        }
    }

    public void add(BinarySortTreeNode node){
        add(root, node);
    }

    /**
     * 查找节点
     * @param node 当前节点
     * @param val 要查找的节点值
     * @return
     */
    public BinarySortTreeNode search(BinarySortTreeNode node, int val) {
        //判断当前节点是否为要找到的值
        if (node.val == val) {
            return node;
        } else if (node.val > val) {
            //如果当前节点大于查找值，就向左递归
            if (node.left == null) {
                return null;
            }
            return search(node.left, val);
        }else {
            //否则就向右递归
            if (node.right == null) {
                return null;
            }
            return search(node.right, val);
        }
    }

    public BinarySortTreeNode search(int val) {
        return search(root, val);
    }

    /**
     * 查找目标节点的父节点
     * @param node 当前节点
     * @param val 要查找的值
     * @return
     */
    private BinarySortTreeNode searchTargetParent(BinarySortTreeNode node, int val) {
        //判断当前节点的子节点是否为目标节点
        boolean isTargetParent = (node.left != null && node.left.val == val) || (node.right != null && node.right.val == val);
        if (isTargetParent) {
            return node;
        } else {
            //如果查找值小于当前节点，向左递归
            if (val < node.val && node.left != null) {
                return searchTargetParent(node.left, val);
            } else if (val >= node.val && node.right != null) {
                //如果查找值大于当前节点,向右递归
                return searchTargetParent(node.right, val);
            } else {
                //否则目标节点不存在
                return null;
            }
        }
    }

    public BinarySortTreeNode searchTargetParent(int val) {
        return searchTargetParent(root, val);
    }

    /**
     * 删除指定节点
     * @param val 要删除节点的值
     */
    public void deleteNode(int val) {
        //判断要删除的是否为根节点
        if (root.val == val && root.left == null && root.right == null) {
            throw new RuntimeException("树中只有根节点，无法删除!");
        }

        //查找目标节点
        BinarySortTreeNode target = search(val);
        if (target == null) {
            return;
        }
        //查找目标节点的父节点
        BinarySortTreeNode parent = searchTargetParent(val);

        //判断要删除的节点的子节点情况
        if (target.left == null && target.right == null) {
            //删除叶子节点
            deleteLeafNode(val, parent);
        } else if (target.left != null && target.right != null) {
            //删除有两颗子树的节点的节点
            deleteTwoBranchNode(target);
        }else {
            //删除只有一颗子树的节点
            deleteOneBranchNode(val, target, parent);
        }
    }

    /**
     * 删除有两颗子树的节点
     * @param target 目标节点
     * @return
     */
    public void deleteTwoBranchNode(BinarySortTreeNode target) {
        BinarySortTreeNode minNodeOfTargetRitht = target.right;
        //遍历找到目标节点右子树上的最小值
        //右子树上的最小值，也就是目标节点的右子节点的左树最大值
        while (minNodeOfTargetRitht.left != null) {
            minNodeOfTargetRitht = minNodeOfTargetRitht.left;
        }
        //删除最小值
        deleteNode(minNodeOfTargetRitht.val);
        //目标节点的值替换为该最小值
        target.val = minNodeOfTargetRitht.val;
    }

    /**
     * 删除只有一颗子树的节点
     * @param val 要删除的节点的值
     * @param target 要删除的节点
     * @param parent 要删除的节点的父节点
     */
    private void deleteOneBranchNode(int val, BinarySortTreeNode target, BinarySortTreeNode parent) {
        //判断要目标节点有左子树还是右子树
        if (target.left != null) {
            //判断是否为根节点
            if (parent == null) {
                //如果是根节点，就直接删除
                root = target.left;
            }else {
                //目标节点只有左子树
                if (parent.left.val == val) {
                    parent.left = target.left;
                }else {
                    parent.right = target.left;
                }
            }
        }else {
            if (parent == null) {
                root = target.right;
            }else {
                //目标节点只有右子树
                if (parent.left.val == val) {
                    parent.left = target.right;
                } else {
                    parent.right = target.right;
                }
            }
        }
    }

    /**
     * 删除叶子节点
     * @param val 要删除的节点的值
     * @param parent 要删除的节点的父节点
     */
    private void deleteLeafNode(int val, BinarySortTreeNode parent) {
        //判断目标节点是父节点左节点还是右节点
        if (parent.right != null && parent.right.val == val) {
            parent.right = null;
        }else {
            parent.left = null;
        }
    }
}

posted @ 2020-07-20 17:13 Createsequence 阅读(332) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

Createsequence