红黑树详解

目录

• 1. Linux 红黑树简介
  • 1.1 Linux 红黑树实现
• 2.《数据结构与算法分析》红黑树
  • 2.1 自底向上插入
  • 2.2 自顶向下的红黑树
  • 2.3 自顶向下的删除
• 参考文献

---

1. Linux 红黑树简介

红黑树是一种自平衡二进制搜索树，用于存储可排序的键/值数据对。这不同于基数树（基数树用于有效存储稀疏数组，因此使用长整数索引插入/访问/删除节点）和哈希表（不保留排序到容易按顺序遍历，并且必须针对特定大小进行调整，rbtrees适当扩展存储任意键的哈希函数）。红黑树类似于AVL树，但提供更快的实时边界插入和删除的最坏情况性能（最多两次旋转和分别旋转三圈以平衡树），虽然为了平衡速度稍慢（但仍为O（log n））

1.1 Linux 红黑树实现

Linux rbtree实现针对速度进行了优化，因此有一个比传统方式更少的间接树实现。而不是使用指针来分隔rb_node和数据。在结构中，rb_node的每个实例都嵌入在其组织的数据结构中。而不是使用比较回调函数指针，用户应该编写自己的树搜索和插入功能，调用提供的rbtree函数。

2.《数据结构与算法分析》红黑树

AVL树流行的另一变种是红黑树。对红黑树的操作最坏情形下花费O(logN)时间。（对于插入操作）一种慎重的非递归实现可以相对容易的完成（与AVL树相比）。红黑树是具有下列着色性质的二叉查找树：

1. 每一个节点或者是着成红色，或者是着成黑色
2. 根是黑色的
3. 如果一个节点是红色的，那么它的子节点必须是黑色的
4. 从一个节点到一个NULL指针的每一条路径必须包含相同数目的黑色节点

着色法则的一个推论是，红黑树的高度最多是2log(N+1).因此查找保证是一种对数的操作。困难在于将一个新项插入到树中。通常把新项作为树叶放到树中，如果我们把它涂成黑色，就违反了条件4.因为会建立一条更长的黑节点的路径。所以这一项必须涂成红色，如果它的父节点是黑的，我们插入完成。如果它的父节点已经是红色的，那么就违反了条件3.这时我们必须调整该数以确保条件3满足（又不引起条件4被破坏）。完成这项任务的基本操作是颜色的改变和树的旋转。

2.1 自底向上插入

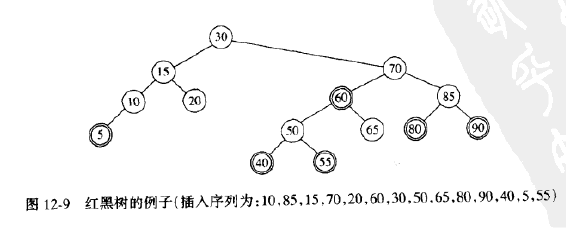
如果向如下图所示，插入25，则非常简单，因为父节点是黑色节点

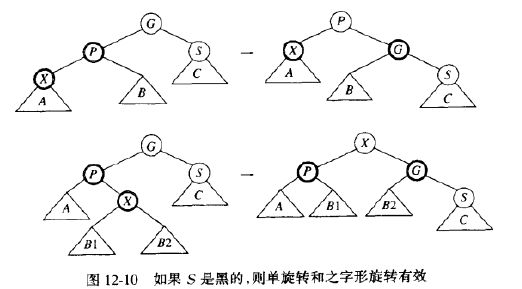
如果父节点是红色的，那么有几种情形（每种都有一个镜像对称）需要考虑。首先，假设这个父节点的兄弟是黑的（约定：NULL节点都是黑色的）。这对于插入3或8是适用的，但对插入99不适用。令X是新加的树叶，P是它的父节点，S是该节点的兄弟（若存在）,G是祖父节点。这种情形只有X和P是红的，G是黑的，因为否则就会在插入前有两个相连的红色节点，违反了红黑树的法则。X,P,G可以形成一个一字形链或之字形链（两个方向中的任一个方向）

12-10展示了当P是左儿子时（还有一个对称情况），该如何旋转和更改着色该树。第一种情形对应P和G之间的单旋转，第二种情形对应双旋转，双旋转首先在X和P之间进行，然后在X和G之间进行。当编写程序的时候，我们必须记录父节点、祖父节点，以及为了重新连接还要记录曾祖父节点。两种情形下，子树的新根均被涂成黑色，因此即使原来的曾祖是红色的，我们也排除了两个相邻红节点的可能性。同样重要的是，这些旋转的结果是通向A,B和C诸路径上的黑节点个数保持不变。如果我们企图将79插入到图12-9中，如果S是红色的，初始时从子树的根到C的路径上有一个黑色节点，在旋转之后，一定仍然还是只有一个黑色节点。两种情况下，在通向C的路径上都有三个节点（新的根，G和S）。由于只有一个可能是黑的，且我们不能有连续的红色节点，我们必须把S和子数的新根都涂成红色，而把G（以及第四个节点）都涂成黑色。但是如果曾祖父也是红色的，那么我们可以将这个过程朝着根的方向上滤，就像对B树和二叉堆所做的那样，直到我们不再有两个相连的红色节点或者到达根（它将被重新涂成黑色）处为止

2.2 自顶向下的红黑树

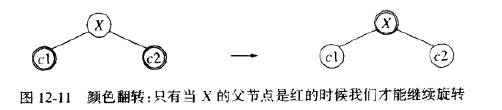
上滤的实现需要用一个栈或用一些父指针保存路径。如果使用一个自顶向下的过程，实际上是对红黑树应用从顶向下保证S不会是红的过程，则伸展树会更有效。在向下的过程中，当我们看到一个节点X有两个红儿子的时候，我们让X成为红的而让它的两个儿子成为黑的。只有当X的父节点P也是红的时候这种翻转将破坏红黑的法则，此时我们可以进行12-10中那样适当的旋转。如果X的父节点的兄弟是红的会如何，这种可能已经被从顶向下过程中的行动所排除。因此X的父节点的兄弟不可能是红的。如果在沿树向下的过程中我们看到一个节点Y有两个红儿子，那我们知道Y的孙子必然是黑的。由于Y的儿子也要变成黑的，甚至在可能发生的旋转之后，因此我们将不会看到两层上另外的红节点。这样，当我们看到X，若X的父节点是红的，则X的父节点的兄弟不可能也是红的。

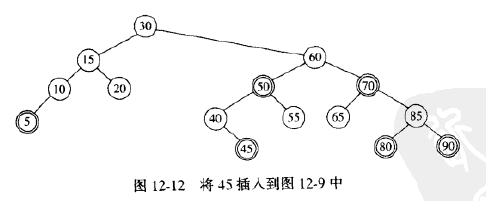
我们假设要将45插入到图12-9中的树上，在沿树向下的过程中，我们看到50有两个红儿子。因此，我们执行一次颜色翻转，使50为红的，40和55是黑的。现在50和60都是红的，我们在60和70之间执行单旋转，使得60是30的右子树的黑根，而70和50都是红的，如果我们看到在含有两个红儿子的路径上有另外一些节点，那么我们继续，执行同样的操作。当我们到达树叶时，把45作为红节点插入，由于父节点是黑的，因此插入完成。

红黑树常常平衡的很好，平均红黑树大约和平均AVL树一样深，从而查找时间一般接近最优。红黑树的优点是执行插入所需要的开销相对较低，实践中发生的旋转相对较少。红黑树的具体实现是复杂的，不仅因为有大量可能地旋转，而且还因为一些子树可能是空的，以及处理根的特殊的情况（尤其是根没有父亲）。因此我们使用两个标记节点：一个是根，一个是NullNode。它的作用像在伸展树中那样是指示一个NULL指针。根标记将存储关键字负无穷和一个指向真正的根的右指针。为此，查找和打印过程需要调整，递归的历程都很巧妙。我们使用一个隐藏的递归过程，而并不强迫用户传递T->Right。因此用户不必关心头节点。

使用两个标记对树的中序遍历
打印树，关注NULLNode，跳过头部

static void
DoPrint(RedBlackTree T)
{
    if (T != NullNode)
    {
        DoPrint(T->Left);
        Output(T->Element);
        DoPrint(T->Right);
    }
}

void
PrintTree(RedBlackTree T)
{
    DoPrint(T->Right);
}

我们还需要使用户调用历程Initialize来指定头节点。如果构造的是第一棵树，那么Initialize应该再为NullNode分配内存（其后的树可以分享NullNode）

typedef enum ColorType{Red, Blck} ColorType;

struct RedBlackNode
{
    ElementType Element;
    RedBlackTree Left;
    RedBlackTree Right;
    ColorType Color;
};

Position NullNode = NULL; /* Needs initialization */

/* Initialization procedure */
RedBlackTree
Initialize(void)
{
    RedBlackTree T;
    
    if (NullNode == NULL)
    {
        NullNode = malloc (sizeof(struct RedBlackNode));
        if (NullNode == NULL)
            FatalError("Out of space!");
        NullNode->Left = NullNode->Right = NullNode;
        NullNode->Color = Black;
        NullNode->Element = Infinity;
    }
    
    /* Create the header node */
    T = malloc(sizeof(struct RedBlackNode));
    if (T == NULL)
        FatalError("Out of space!");
    T->Element = NegInfinity;
    T->Left = T->Right = NullNode;
    T->Color = Balck;
    
    return T;
}

旋转过程

在X节点处执行旋转，

static Position
Rotate(ElementType Item, Position Parent)
{
    if (Item < Parent->Element)
        return Parent->Left = Item < Parent->Left->Element? SingleRotateWithLeft(Parent->Left) : SingleRotateWithRight(Parent->Left);
    else
        return Parent->Right = Item < Parent->Right->Element?
        SingleRotateWithLeft(Parent->Right) :
        SingleRotateWithRight(Parent->Right);
}

插入过程

static Position X, P, GP, GGP;

static
void HandleReorient(ElementType Item, RedBlackTree T)
{
    X->Color = Red; /* Do the color flip */
    X->Left->Color = Black;
    X->Right->Color = Black;
    
    if (P->Color == Red) /* 必须进行旋转 */
    {
        GP->Color = Red;
        if ((Item < GP->Element) != (Item < P->Element))
            P = Rotate(Item, GP); /* 开始双旋转 */
        X = Rotate(Item, GGP);
        X->Color = Black;
    }
    T->Right->Color = Black; /* Make root black */
}

RedBlackTree
Insert(ElementType Item, RedBlackTree T)
{
    X = P = GP = T;
    NullNode->Element = Item;
    while (X->Element != Item)
    {
        GGP = GP;
        GP = P;
        P = X;
        
        if (Item < X->Element)
            X = X->Left;
        else
            X = X->Right;
        if (X->Left->Color == Red && X->Right->Color == Red)
            HandleReorient(Item, T);
    }
    
    if (X != NullNode)
        return NullNode; /* Duplicate */
    X = malloc(sizeof(struct RedBlackNode));
    if (X == NULL)
        FatalError("Out of space!");
    X->Element = Item;
    X->Left = X->Right = NullNode;
    
    if (Item < P->Element) /* Attach to its parent */
        P->Left = X;
    else
        P->Right = X;
    
    HandleReorient(Item, T); / * Color red: 可能需要旋转 */
    
    return T;
}

2.3 自顶向下的删除

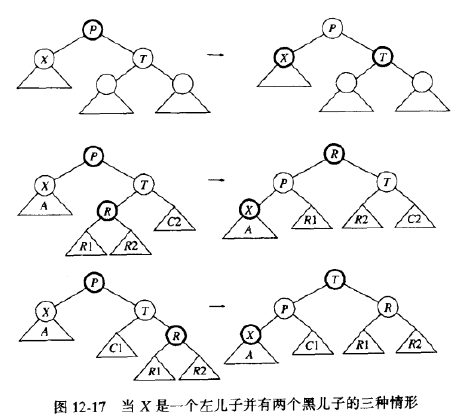
红黑树中的删除也可以自顶向下进行，每一件工作都归结于能够删除一片树叶。因为要删除一个带有两个儿子的节点，我们用右子树上的最小节点代替他。该节点必然最多只有一个儿子，然后将该节点删除。只有一个右儿子的节点可以用相同的方式删除，而只有一个左儿子的节点通过用其左子树上最大节点替换，然后可将该节点删除。对于红黑树，我们使用的方法绕过带有一个儿子的节点的情形，因为这可能在树的中部连接两个红色节点，为红黑条件的实现增加困难。
红色树叶的删除很简单，如果一片树叶是黑的，删除会变复杂，因为黑色节点的删除将破坏条件4.解决办法是保证从上到下删除期间树叶是红的。令X为当前节点，T是它的兄弟，而P是他们的父亲。开始时我们把树的根部涂成红色。当沿树向下遍历时，我们设法保证X是红色的，当我们到达一个新的节点时，我们要去确信P是红的。并且X和T是黑的（因为我们不能有两个相连的红色节点）。存在两种主要的情形：
首先，设X有两个黑儿子，此时有三种子情况，如果T也有两个黑儿子，那么我们可以翻转X，T和P的颜色来保持这种不变性，否则，T的儿子之一是红的，根据这个儿子节点是哪一个，可以应用下图第二和第三种情形表示的旋转。注意这种情形对于树叶将是适用的，因为NullNode被认为是黑的。设X的儿子之一是红的，在这种情形下，我们落到下一层上，得到新的X，T和P。如果X落在红儿子上，我们可以继续向前进行。如果不是这样，我们知道T将是红的，而X和P将是黑的。我们可以旋转T和P，使得X的新父亲是红的，X和他的祖父将是黑的，此时可以回到第一种主情况。

参考文献

1. Mark Allen Weiss.数据结构与算法分析[M].America, 2007
2. Linux红黑树说明文档-linux/Documentation/rbtree.txt
3. 红黑树解析与移植-https://blog.csdn.net/npy_lp/article/details/7420689
4. 红黑树与AVL树优劣-https://www.zhihu.com/question/19856999
5. 红黑树平衡原理解析-https://my.oschina.net/u/4543837/blog/4406384

---

本文作者: CrazyCatJack

本文链接: https://www.cnblogs.com/CrazyCatJack/p/14408192.html

版权声明:本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！

关注博主:如果您觉得该文章对您有帮助，可以点击文章右下角推荐一下，您的支持将成为我最大的动力！

---