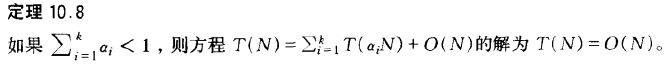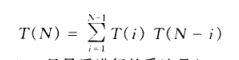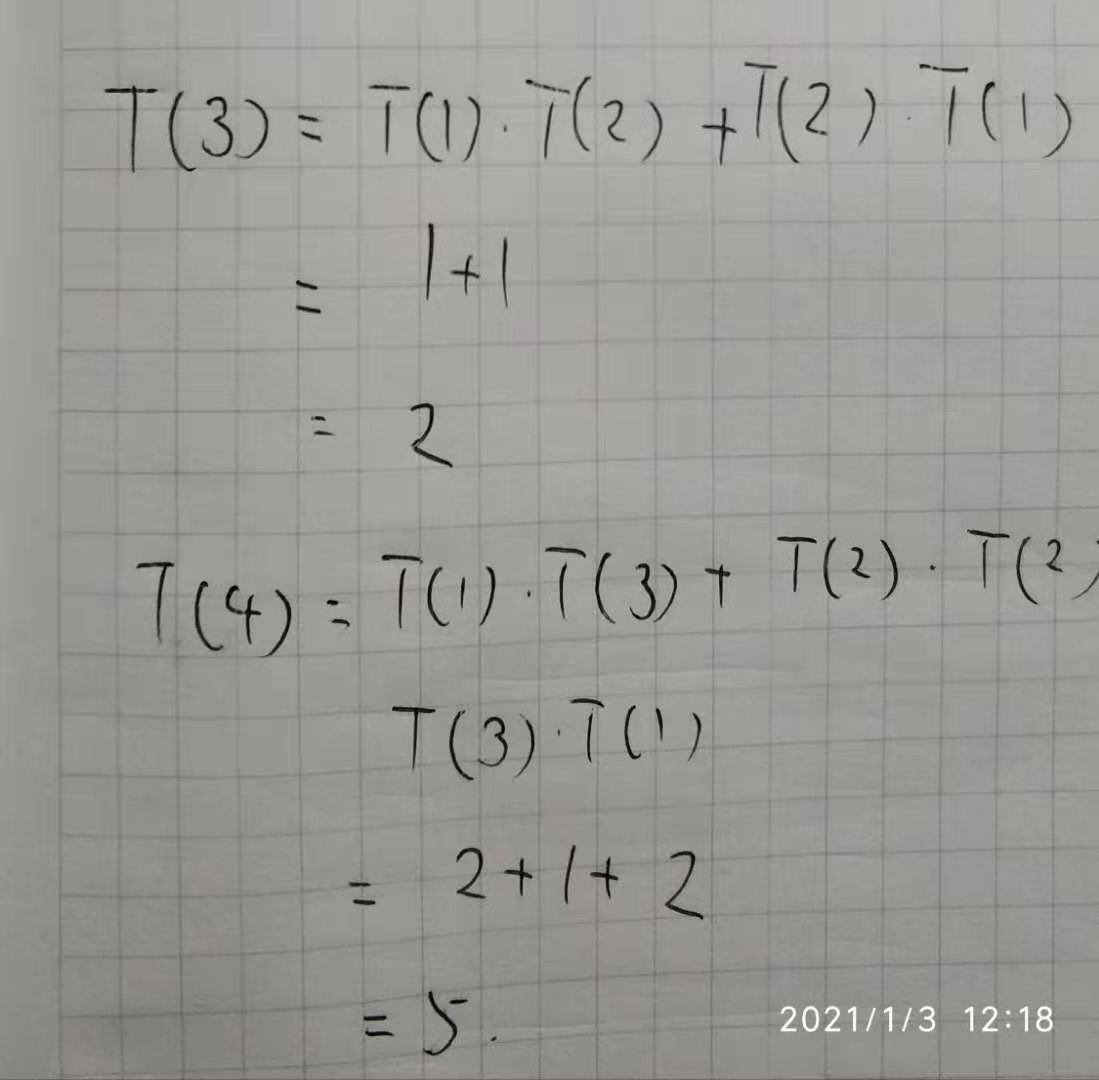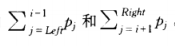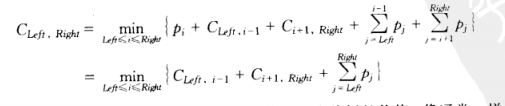《数据结构与算法分析》学习笔记-第十章-算法设计技巧

10.1 贪婪算法

贪婪算法分阶段的工作，在每个阶段，可以认为所做决定是最好的，而不考虑将来的后果。一般来说，这意味着选择的是某个局部的最优。当算法终止时，我们希望局部最优就是全局最优。如果是这样的话，那么算法就是正确的，否则，算法得到的是一个次最优解。如果不要求绝对最佳答案，那么有时用简单的贪婪算法生成近似答案，而不是使用一般来说产生准确答案所需要的复杂算法。

10.1.1 调度问题

10.1.1.1 单处理器

设有作业j1,j2,j3,j4，其对应的运行时间分别为t1,t2,t3,t4.而处理器只有一个。为了把作业的平均完成的时间最小化，调度这些作业最优的顺序是什么。如果按照顺序调度，那么调度作业的平均时间为：

t1
t1+t2
t1+t2+t3
t1+t2+t3+t4
求和：4t1+3t2+2t3+t4
求平均调度时间：4t1+3t2+2t3+t4/4

显而易见，如果希望平均调度时间最优，那么就要优先做耗时较短的工作，因此操作系统调度程序一般把优先权赋予那些更短的作业。

10.1.1.2 多处理器

让最短的作业先运行，按照作业运行时间从短到长的顺序，依次轮流让不同的处理器进行处理

CPU1 j1 j4 j7
CPU2 j2 j5 j8
CPU3 j3 j6 j9

之前的操作都是将平均调度时间最小化，如果想将最后完成时间最小化就不是很容易，即让整个序列完成的时间更早。

10.1.2 Huffman编码

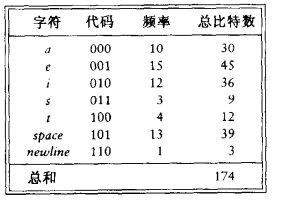
文件压缩中常见。ASCII码中有100个左右可打印字符。那么可以用log100个bit来表示。对于压缩文件中只使用了某些字符，那么可以通过更少的Bit来表示。例如图中向左分支是0，向右分支是1，那么a为000，c为001,以此类推。

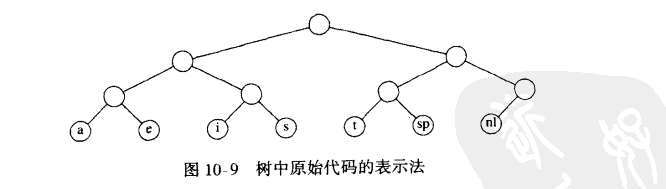
由于newline没有右兄弟，因此上移，将树变成满树

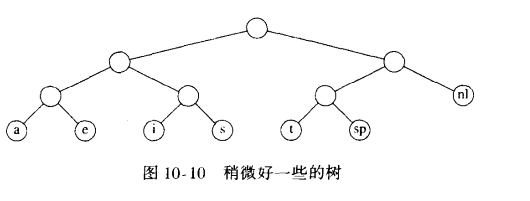
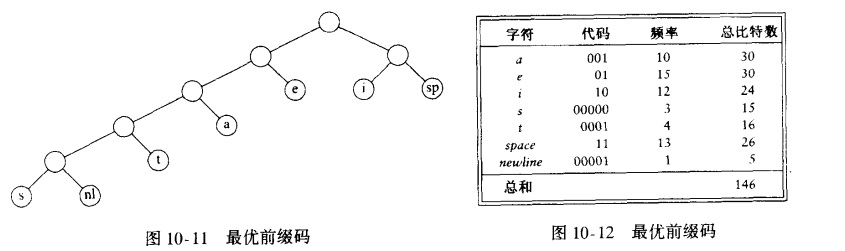
满树：所有的节点，要么是树叶，要么有两个儿子。一种最优的编码将总具有这个性质，否则就像上面，具有一个儿子的节点可以向上移动一层。如果字符都只放在树叶上，那么任何比特序列总能够被毫无歧义的译码。并且，这些字符代码的长度是否不同并不要紧，只要没有字符代码是别的字符代码的前缀即可。这种编码叫做前缀码。反之，如果一个字符放在非树叶节点上，那就不能够保证译码没有二义性。可以想见，如果想要以最小的空间表示最多的字符，那么就要将出现频率高的字符，放到尽可能浅的深度，而出现频率低的字符，可以放到深的深度。

哈夫曼算法

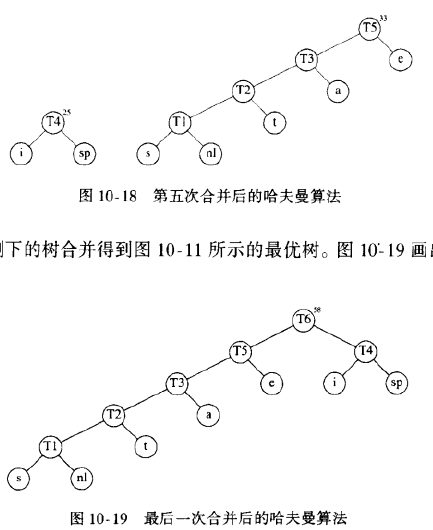
假设字符的个数为C，哈夫曼算法可以描述如下：算法对一个由树组成的森林进行。一棵树的权等于它的树叶的频率的和。任意选取最小权的两棵树T1和T2，并任意形成以T1和T2为子树的新树，将这样的过程进行C-1次。在算法的开始，存在C棵单节点数。每个字符一棵。在算法结束时得到一棵树，这棵树就是最优哈弗曼编码树。

初始阶段，每个元素看成一棵单节点树。每个节点有自己的value和权重。
将当前森林中，权值最低的两棵树进行合并，合并后新树的权值是老树权值的和
继续进行第二步，不断将当前森林中权值最低的两棵树进行合并，合并时，左右分支任意，可以互换
可以看出，权值（出现频率）越低，其深度越深；权值越高，其深度越浅。这样就能保证总开销最小。

该算法是贪婪算法的原因在于，在每一阶段我们都进行一次合并而没有进行全局的考虑，我们只是选择两棵权值最小的树进行合并。我们可以依权排序将这些树保存在一个优先队列中。那么对于元素个数不超过C的优先队列将进行一次BuildHeap, 2C-2次DeleteMin和C-2次Insert，因此运行时间伟O(ClogC)。如果不使用优先队列，而是链表的话，将给出一个O(C^2)的算法。优先队列实现方法的选择取决于C有多大。

10.1.3 近似装箱问题

联机：必须解决当前问题，流程才能继续
脱机：必须了解完所有的问题，流程才能开始

10.1.3.1 联机算法

对于联机装箱问题不存在最优算法。联机算法从不知道输入何时会结束，因此它提供的性能保证必须在整个算法的每一时刻成立。

定理：存在使得任意联机装箱算法至少使用4/3最优箱子数的输入

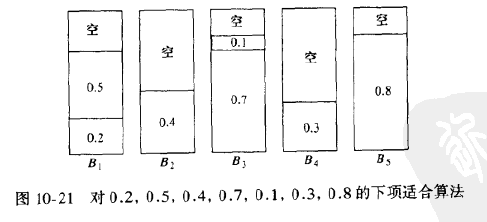
1. 下项适合算法

当处理任何一项物品时，我们检查看它是否能装进刚刚装进物品的同一个箱子中去。如果能够装进去，那么就把它放入该箱中。否则就开辟一个新箱子。该算法能够以线性时间运行。

令M是将一列物品I装箱所需的最优装箱数，则下项适合算法所用箱数绝不超过2M个箱子。存在一些顺序使得下项适合算法用箱2M-2个

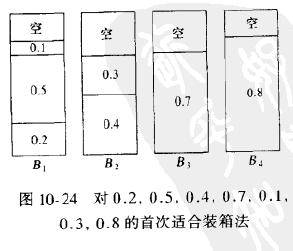
2. 首次适合算法

虽然下项适合算法有一个合理的性能保证。但是它的实践效果却很差，因为在不需要开辟新箱子的时候，它却开辟了新的箱子。首次适合算法的策略是依序扫描这些箱子，但把新的一项物品放入足够盛下它的第一个箱子中。因此，只有当先前放置物品的结果已经没有再容下当前物品余地的时候，我们才开辟一个新的箱子。首次适合算法保证其解最多包含最优装箱数的二倍。当首次适合算法对大量其大小均匀分布在0和1之间的物品进行运算时，经验结果指出，首次适合算法用到大约比最优装箱方法多2%的箱子，这是完全可以接受的

3. 最佳适合算法

该法不是把一项新物品放入所发现的第一个能容纳它的箱子，而是放到所有箱子中能容纳它的最满的箱子中。最佳适合算法比起最优算法，绝不会坏过1.7倍左右

10.1.3.2 脱机算法

如果能够观察全部物品之后再算出答案，那么应该会做的更好。所有联机算法的主要问题在于将大项物品装箱困难，特别是当他们在输入的晚期出现的时候。因此解决该问题的方法时将各项物品排序，将最大的物品放在最先。此时可以应用首次适合算法或最佳适合算法，分别得到首次适合递减算法和最佳适合递减算法。最佳适合递减算法和首次适合递减算法的效果差不多。

令N项物品的输入大小（以递减顺序排序）分别为s1, s2, ... , sN。并设最优装箱方法使用M个箱子。那么，首次适合递减算法放到外加的箱子中的所有物品的大小最多为1/3
放入外加的箱子中的物品的个数最多是M-1
令M时物品集I装箱所需的最优箱子数，则首次适合递减算法所用箱子数绝不超过(4M+1)/3
令M是将物品集I装箱所需要的最优箱子数，则首次适合递减算法所用箱子数绝不超过11/9 * M + 4。存在使得首次适合递减算法用到11/9 * M个箱子的序列

10.2 分治算法

分：递归解决较小的问题（基本情况除外）
治：从子问题的解，构建原问题的解

10.2.1 分治算法的运行时间

所有有效的分治算法都是把问题分成一些子问题，每个子问题都是原问题的一部分。然后进行某些附加的工作以算出最后的答案。

方程T(N)=aT(N/b)+Θ(N^k)的解为
T(N)=
O(N^(log(b)a)), 若a>b^k
O(N^k * logN), 若a=b^k
O(N^k), 若a<b^k
其中a>=1, b>1

方程T(N)=aT(N/b)+Θ(N^k * (logN)^p)的解为
T(N)=
O(N^(log(b)a)), 若a>b^k
O(N^k * (logN)^(p+1)), 若a=b^k
O(N^k * (logN)^p), 若a<b^k
a >=1, b> 1 且p >=0

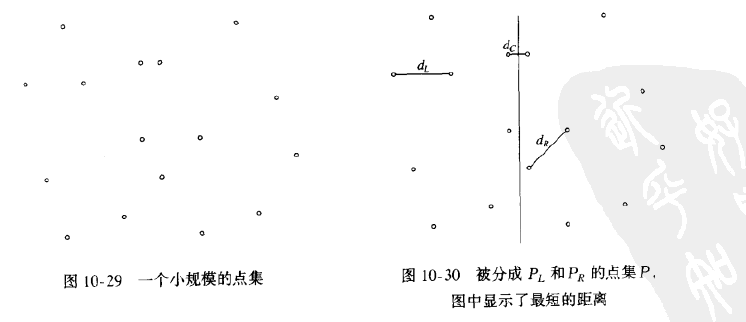
10.2.2 最近点问题

平面上有点列P，如果p1=(x1,y1), p2=(x2,y2)，那么p1和p2间欧几里得距离为[(x1-x2)^2 + (y1-y2)^2](1/2)。我们需要找出一对距离最近的点。将这些点按照x的坐标排序，画一条垂线，将点集分为两半：PL和PR，最近的一对点或者都在PL中，或者都在PR中，或者一个在PL而另一个在PR中。这三个距离分别叫做dL、dR和dC

蛮力计算

for(i = 0; i<NumPointsInStrip; i++)
    for(j=i+1; j<NumPointsInStrip; j++)
        if(Distance(Pi, Pj) < x)
            x = Distance(Pi,Pj);

精炼计算

for(i = 0; i<NumPointsInStrip; i++)
    for(j=i+1; j<NumPointsInStrip; j++)
        if (Pi和Pj的y坐标相差大于x)
            break;
        else
            if(Distance(Pi, Pj) < x)
                x = Distance(Pi,Pj);

10.2.3 选择问题

要求找出含N个元素的表S中的第k个小的元素。基本的算法是简单递归策略。设N大于截止点，在截止点后元素将进行简单的排序。v是选出的一个元素，叫做枢纽元。其余的元素被放在两个集合S1和S2中。S1含有那些不大于v的元素，而S2则包含那些不小于v的元素。如果k <= |S1|，那么S中的第k个最小的元素，可以通过递归的计算S1中第k个最小的元素而找到。如果k=|S1|+1，则枢纽元就是第k个最小的元素。否则，在S中第k个最小的元素是S2中的第（k-|S1|-1）个最小元素。这个算法和快速排序之间的主要区别在于，这里要求解的只有一个子问题而不是两个子问题。为了保证快速的选择出好枢纽元，关键想法是再用一个间接层。我们不是从随即元素的样本中找出中项，而是从中项的样本中找出中项。

把N个元素分成[N/5]组，5个元素一组，忽略（最多4个）剩余的元素
找出每组的中项，得到[N/5]个中项的表M
求出M的中项，将其作为枢纽元V返回

使用五分化中项的中项的快速选择算法的运行时间为O(N)。分治算法还可以用来降低选择算法预计所需要的比较次数

10.2.4 一些运算问题的理论改进

10.2.4.1 整数相乘

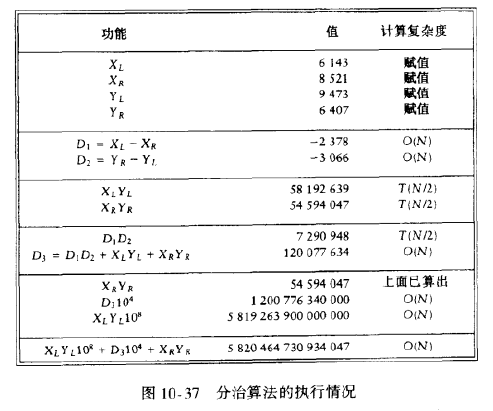
假设想要将两个N位数X和Y相乘。如果X和Y恰好有一个是负的，那么结果就是负的，否则结果为正数。因此可以进行这种检查然后假设X, Y >= 0。设X=61438521，Y=94736407。我们将X和Y拆成两半。分别由最高几位和最低几位数字组成。XL=6143，XR=8521，YL=9473，YR=6407.我们还有X=XL10^{4+XR和Y=YL10}4+YR。由此得到：XY=XLYL10^{8+（XLYR+XRYL）10}4+XRYR。该方程由四次乘法组成。即XLYL、XLYR、XRYL、XRYR。它们每一个都是原问题大小的一般（N/2数字）。用10^8和104做乘法实际就是添加一些0，这及其后的几次加法只是添加了O(N)附加的工作。如果我们递归地使用该算法进行这四项乘法，在一个适当的基本情形下停止，我们得到递归：T(N)=4T(N/2)+O(N)。根据定理，可以看到T(N)=O(N^2)。为了得到一个亚二次的算法，我们必须使用少于四次的递归调用.关键在于XLYR+XRYL=(XL-XR)(YR-YL)+XLYL+XRYR。这样通过三次递归调用即可得出结果。

现在的递归方程满足：T(N)=3T(N/2)+O(N)，根据定理，得到T(N)=O(N^(log(2)3)) = O(N^1.59)。未完成这个算法，我们必须要有一个基准情况，该情况可以无需递归而解决。当两个数都是一位数字时，可以通过查表进行乘法，若有一个乘数为0，则我们返回0.假如我们在实践中要用这种算法，我们将选择对机器最方便的情况作为基本情况。

10.2.4.2 矩阵乘法

当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。
矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。
乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

简单的O(N^3)矩阵乘法

void
MatrixMultiply(Matrix A, Matrix B, Matrix C, int N)
{
    int i, j, k;
    
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            C[i][j] = 0;
    
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
            for (k = 0; k < N; k++)
                C[i][j] += A[i][k] * B[k][j];
}

10.3 动态规划

一个可以被数学上递归表示的问题也可以表示成一个递归算法，在许多情形下对朴素的穷举搜索得到显著的性能改进。任何数学递归公式都可以直接翻译成递归算法，但是基本现实是编译器常常不能正确对待递归算法，结果导致低效的算法。当我们怀疑很可能是这种情况时，必须再给编译器提供一些帮助，将递归算法重新写成非递归算法，让编译器把那些子问题的答案系统的记录在一个表内，利用这种方法的一种技巧叫做动态规划。

10.3.1 用一个表代替递归

斐波那契数的低效算法

int
Fib(int N)
{
    if (N <= 1)
        return 1;
    else
        return Fib(N - 1) + Fib(N - 2);
}

该算法慢的原因在于冗余计算，且荣誉计算的增长是爆炸性的，如果编译器的递归模拟算法要是能够保留一个预先算出的值的表而对已经解过的子问题不再进行递归调用。那么这种指数式的爆炸增长就可以避免。

斐波那契数的线性算法

int
Fibonacci(int N)
{
    int i, Last, NextToLast, Answer;
    
    if (N <= 1)
        return 1;
    
    Last = NextToLast = 1;
    for (i = 2; i <= N; i++)
    {
        Answer = Last + NextToLast;
        NextToLast = Last;
        Last = Answer;
    }
    
    return Answer;
}

10.3.2 矩阵乘法的顺序安排

设有四个矩阵ABC和D。不同的相乘顺序导致计算次数完全不同，导致效率完全不同。最好的排列顺序方法大约只用了最坏的排列顺序方法的九分之一的惩罚次数。我们定义T(N)是顺序的个数，此时T(1)=T(2)=1, T(3)=2,而T(4)=5.

设mLeft, Right是进行矩阵乘法ALeftALeft+1 ... ARight-1ARight所需要的乘法次数，为方便起见，mLeft,Left=0.设最后的乘法是(ALeft...Ai)(Ai+1...ARight)，其中Left<=i<Right。此时所用的乘法次数为mLeft,i+mi+1,Right+cLeft-1cicRight。这三项分别代表计算（Aleft...Ai）、(Ai+1...ARight)以及它们的乘积所需要的乘法。如果我们定义MLeft,Right为在最优排列顺序下所需要的乘法次数，那么，若Left<Right，则：

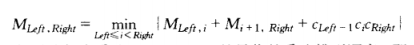
这个方程意味着，如果我们有乘法ALeft...ARight的最优的乘法排列顺序，那么子问题ALeft...Ai和Ai+1...ARight就不能次最优的执行。否则我们可以通过用最优的计算代替次最优计算而改进整个结果。
这个公式可以直接翻译成递归程序，这样的程序将是明显低效的，由于大约只有MLeft,Right的N^2/2个值需要计算，因此显然可以用一个表来存放这些值。进一步的考察表明，如果Right-Left=k，那么只有在MLeft,Right的计算中所需要的那些值Mx,y满足y-x<k。这告诉我们计算这个表所需要使用的顺序。如果除最后答案M1,N外我们还想要显示实际的乘法顺序，那么我们可以使用第九章中的最短路径算法的思路，无论何时改变MLeft,Right，我们都要记录i的值，这个值是重要的。

找出矩阵乘法最优顺序的程序
void
OptMatrix(const long C[], int N, TwoDimArray M, TwoDimArray LastChange)
{
    int i, k, Left, Right;
    long ThisM;
    
    for (Left = 1; Left <=N; Left++)
        M[Left][Left] = 0;
    for (k = 1; k < N; k++)
        for (Left = 1; Left <= N-k; Left++)
        {
            /* for each position */
            Right = Left + k;
            M[Left][Right] = Infinity;
            for (i = Left; i < Right; i++)
            {
                ThisM = M[Left][i] + M[i+1][Right] + C[Left - 1]*C[i]*C[Right];
                if (ThisM < M[Left][Right])
                {
                    M[Left][Right] = ThisM;
                    LastChange[Left][Right] = i;
                }
            }
        }
}

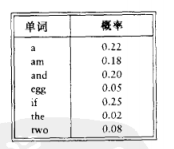
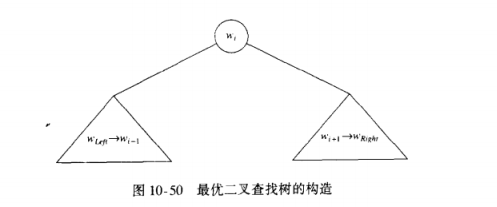
10.3.3 最优二叉查找树

给定一列单词w1, w2, ... wN和他们出现的固定的概率p1, p2, ... pN。问题是要以一种方法在一棵二叉查找树中安放这些单词使得总的期望存取时间最小。在一棵二叉查找树中，访问深度d处的一个元素所需要的比较次数是d+1，因此如果wi被放在深度di上，那么我们就要将

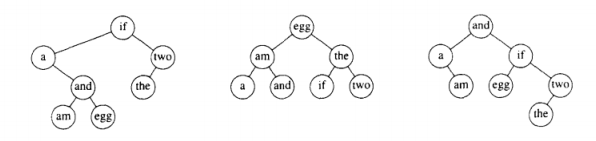
假设样本输入如下：

第一棵树是是用贪婪方法形成的，存取概率最高的单词被放在根节点处。然后左右子树递归形成。第二棵树是理想平衡查找树。这两棵树都不是最优的，由第三棵树的存在可以证实。

最优二叉树的构造：

如果Left > Right，那么树的开销是0，这就是NULL情形，对于二叉查找树我们总有这种情形，否则，根花费pi，左子树的代价相对于它的根为Cleft,i-1，右子树相对于它的根的代价为Ci+1,Right,这两棵树的每个节点从wi开始都比从它们对应的根开始深一层。因此我们必须加

由此得到公式：

10.3.4 所有点对最短路径

计算有向图G=(V,E)中每一点时间赋权最短路径的一个算法。在第九章我们看到单发点最短路径问题的一个算法，该算法找出从任意一点s到所有其他顶点的最短路径。该算法（Dijkstra）对稠密的图以O(|V|^{2)时间运行，实际上对稀疏的图更快。这里将给出一个较小的算法解决对稠密图的所有点对的问题，该算法的运行时间为O(|V|}3),他不是对Dijkstra算法|V|次迭代的一种渐进改进，但对非常稠密的图可能更快，原因是它的循环更紧凑。如果存在一些负的边值但没有负值圈，那么这个算法也能正确运行，而Dijkstra算法此时是失败的。Dijkstra算法在顶点s开始并分阶段工作。图中的每个顶点最终都要被选作中间结点。如果当前所选的顶点是v，那么对于每个w属于V，置dw=min(dw, dv+cv,w)，这个公式是说，从s到w的最佳举例或者是从前面知道的从s到w的举例，或者是从s（最优的）到v然后在直接从v到w的结果。Dijkstra算法提供了动态规划算法的想法。我们依序选择这些顶点。我们将Dk,i,j定义为从vi到vj只使用v1,v2,...vk作为中间顶点的最短路径的权。根据这个定义，D0,i,j=ci,j。其中若（vi, vj）不是该图的边则ci,j是无穷。再有，根据定义，D|V|,i,j是图中从vi到vj的最短路径。当k>0时，我们可以给Dk,i,j写出一个简单公式。从vi到vj只使用v1,v2,...vk作为中间顶点的最短路径或者根本不使用vk作为中间顶点的最短路径，或者是由两条路景vi->vk和vk->vj合并而成的最短路径。其中每条路径只使用前k-1个顶点作为中间顶点。得出公式：Dk,i,j=min{Dk-1,i,j, Dk-1,i,k+Dk-1,k,j}。实践需求还是O(|V|^3),跟前面的两个动态规划例子不同，这个时间界实际上尚未用另外的方法降低。因为第k阶段只依赖于第k-1阶段，所以看来只有两个|V|*|V|矩阵需要保存，然而，在用k开始或结束的路径上以k作为中间顶点对结果没有改进，除非存在一个负的圈。因此只有一个矩阵是必须的，因为Dk-1,i,k=Dk,i,k和Dk-1,k,j=Dk,k,j。这意味着右边的项都不改变值且都不需要存储。这个观察结果导致图中的简单程序。在一个完全图中，每一对顶点（两个方向上）都是联通的，该算法几乎肯定要比Dijkstra算法的|V|次迭代快，因为这里的循环非常紧凑并适合并行计算。

void
AllPairs(TwoDimArray A, TwoDimArrayD, TwoDimArray Path, int N)
{
    int i, j, k;
    
    /* Initialize D and Path */
    for (i = 0; i < N; i++)
        for (j = 0; j < N; j++)
        {
            D[i][j] = A[i][j];
            Path[i][j] = NotAVertex;
        }
    
    for (k = 0; k < N; k++)
        /* Consider each vertex as an intermediate */
        for (i = 0; i < N; i++)
            for (j = 0; j < N; j++)
                if (D[i][k] + D[k][j] < D[i][j])
                {
                    /* Update shortest path */
                    D[i][j] = D[i][k] + D[k][j];
                    Path[i][k] = k;
                }
}

动态规划是强大的算法设计技巧，它给解提供一个起点，它基本上是首先求解一些更简单问题的分治算法的范例，重要的区别在于这些更简单的问题不是原问题的明确的分割。因为子问题反复被求解，所以重要的是将它们的解记录在一个表中而不是重新计算它们。在某些情况下，解可以被改进（这确实不总是明显鹅，而且常常是困难的）。在另一些情况下，动态规划方法则是所知道的最好的处理方法。在某种意义上，如果你看出一个动态规划问题，那么你就看出所有的问题。

10.4 随机化算法

在算法期间，随机数至少有一次用于决策。该算法的运行时间不只依赖于特定的输入，而且依赖于所发生的随机数。一个随机化算法的最坏运行时间几乎总是和非随机化算法的最坏情形运行时间相同，区别在于，好的随机化算法没有不好的输入，而只有坏的随机数（相对于特定的输入）。例如快速排序中枢纽元的选择，方法A选第一个元素，方法B随机选出一个元素。两种最坏情形之间的区别在于，存在特定的输入总能够出现在A中并产生不好的运行时间。当每一次给定已排序数据时，方法A总是会以最坏运行时间运行（O(N^2)）。如果方法B以相同的输入运行两次，它将有两个不同的运行时间。在运行时间的计算中，我们假设所有的输入都是等可能的，实际上这并不成立。例如排序的输入常常要比统计上期望的出现的多得多。这会产生一些问题，特别是对于快速排序和二叉查找树。通过使用随机化算法，特定的输入不再是重要的。重要的是随机数，我们可以得到一个期望的运行时间，此时我们是对所有可能的随机数取平均而不是对所有可能的输入取平均。使用随机枢纽元的快速排序算法是一个O(NlogN)期望时间算法，这就是说，对任意的输入，包括已经排序的输入，运行时间的期望值为O(NlogN)。期望运行时间界要多少强于平均时间界，比对应的最坏情形界弱。得到最坏情形时间界的那些解决方案常常不如他们的平均情形那样在实际中常见、但是随机化算法却通常是一致的。

参考文献

Mark Allen Weiss.数据结构与算法分析[M].America, 2007

本文作者: CrazyCatJack

本文链接: https://www.cnblogs.com/CrazyCatJack/p/14408191.html

关注博主:如果您觉得该文章对您有帮助，可以点击文章右下角推荐一下，您的支持将成为我最大的动力！

posted @ 2021-02-20 23:29 CrazyCatJack 阅读(641) 评论(0) 编辑收藏举报

刷新页面返回顶部

CrazyCatJack

我是程序员家的一只猫。每次趁主人出门，我都会冲杯咖啡，打开电脑，猫也来编程！