学习老算法，争做老东西

目录

• 带撤销并查集
• Tarjan
  • SCC
• 线性筛积性函数
• 数论分块
• 莫比乌斯反演
• 欧拉反演
• 常用结论
• 杜教筛
  • 整除集合
  • 块筛
  • Dirichlet 双曲线法
  • 杜教筛
• Dancing Links

---

带撤销并查集

只是来贴个板子，没什么好讲的。

带撤销并查集

struct DSU
{
	int n=0,tot=0,fa[MAXN],siz[MAXN],s[MAXN];

	void ins() { n++,fa[n]=n,siz[n]=1; }

	int get(int x) { return fa[x]==x?x:get(fa[x]); }

	void merge(int x,int y)
	{
		x=get(x),y=get(y);
		if (x==y) return;
		if (siz[x]<siz[y]) swap(x,y);
		s[++tot]=y,fa[y]=x,siz[x]+=siz[y];
	}

	void undo()
	{
		if (!tot) return;
		int y=s[tot--];
		siz[fa[y]]-=siz[y];
		fa[y]=y;
	}

	void back(int t=0) { while (tot>t) undo(); }
};

虚假的1800，真正的板子题

---

Tarjan

SCC

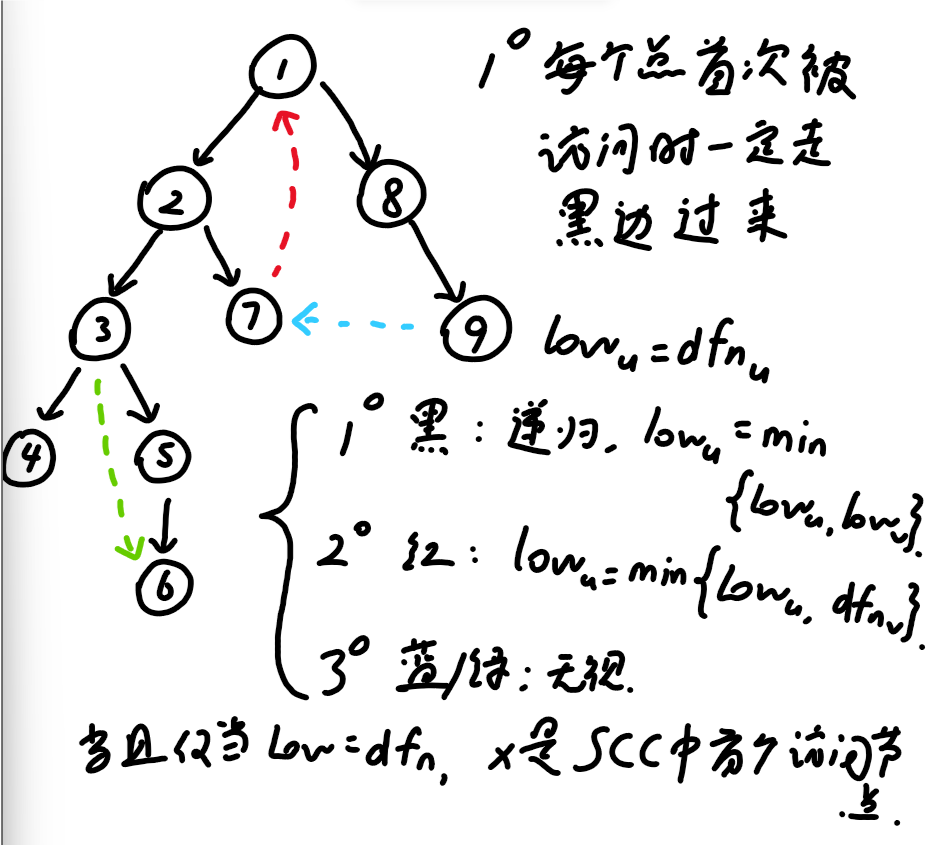
SCC

struct SCC
{
	int n,cur,cnt;
	vector<vector<int>> adj;
	vector<int> stk,dfn,low,bel;

	SCC() {}
	SCC(int n) { init(n); }

	void init(int n)
	{
		this->n=n;
		adj.assign(n,{});
		stk.clear();
		dfn.assign(n,-1);
		low.resize(n);
		bel.assign(n,-1);
		cur=cnt=0;
	}

	void add(int u,int v) { adj[u].push_back(v); }

	void dfs(int x)
	{
		dfn[x]=low[x]=cur++;
		stk.push_back(x);
		for (auto y:adj[x])
		{
			if (dfn[y]==-1)
			{
				dfs(y);
				low[x]=min(low[x],low[y]);
			}
			else if (bel[y]==-1) low[x]=min(low[x],dfn[y]);
		}
		if (dfn[x]==low[x])
		{
			int y;
			do
			{
				y=stk.back();
				bel[y]=cnt;
				stk.pop_back();
			} while (y!=x);
			cnt++;
		}
	}

	vector<int> work()
	{
		for (int i=0;i<n;i++)
			if (dfn[i]==-1) dfs(i);
		return bel;
	}
};

---

线性筛积性函数

这一做法仅限于能在 \(\mathcal{O}(\ln n)\) 时间内计算任意一个 \(f(p^m)\) 的数论函数。

维护这样一个函数 \(g\)，欧筛中筛去 i*pri[j] 时：

1. 若 i%pri[j]==0 则 g[i*pri[j]]=g[i]*pri[j]。

2. 否则，g[i*pri[j]]=p。

那么当且仅当 \(n\) 为某质数的幂时，\(n=g_n\)，这些位置的 \(f\) 我们在 \(\mathcal{O}(\ln{n})\) 时间内计算，其余位置根据积性函数性质计算，即可在 \(\mathcal{O}(n)\) 时间内得到 \(f\) 的前 \(n\) 项。

---

数论分块

考虑这样一个问题：求 \(\sum_{i=1}^nf(i)\lfloor\frac{n}{i}\rfloor\)，我们默认此处的 \(f(i)\) 已知。

暴力做是 \(\mathcal{O}(n)\) 的，但题目中往往需要一个 \(\mathcal{O}(\sqrt{n})\) 的做法。

当 \(1 \leq i \leq \sqrt{n}\) 时，这部分我们暴力解决即可。

当 \(i \geq \sqrt{n}\) 时，有 \(1 \leq \lfloor\frac{n}{i}\rfloor \leq \sqrt{n}\)，如果我们对 \(f(i)\) 先做前缀和，便可以对 \(\lfloor\frac{n}{i}\rfloor\) 相同的 \(i\) 打包整块求和。

现在问题是，怎样 \(\mathcal{O}(1)\) 地找到当前块的终点/下一块的起始点。

幸运地，我们有下面的发现：

1. \(\lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor}\rfloor \geq \lfloor\frac{n}{\frac{n}{\lfloor\frac{n}{i}\rfloor}}\rfloor = \lfloor\frac{n}{i}\rfloor \geq \lfloor\frac{n}{\lfloor\frac{n}{\frac{n}{i}}\rfloor}\rfloor \geq \lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor}\rfloor \to \lfloor\frac{n}{\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor}\rfloor = \lfloor\frac{n}{i}\rfloor\)

2. \(i = \lfloor\frac{n}{\frac{n}{i}}\rfloor \leq \lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\)

所以 \(i\) 与 \(\lfloor\frac{n}{\lfloor\frac{n}{i}\rfloor}\rfloor\) 同块，且后者是块的右端点。

$f(i)=1$ 的模板

int H(int n)
{
	int ret=0;
	for (int l=1,r;l<=n;l=r+1)
	{
		r=n/(n/l);
		ret+=(r-l+1)*(n/l);
	}
	return ret;
}

数论分块问题往往要注意：是否需要开 long long。

做多维复杂度不变，但要注意 l 上界只能取到 min(n,m)，偷懒写 n 在 \(n \leq m\) 时会 RE。

实际上对上述问题一个更加自然的想法是：根号两边的值会相等，我们只算根号内的那部分，翻倍后减去重合的部分（即容斥处理）。

考虑更一般的情况，比如计算一个平凡的 \(\text{Dirichlet}\) 卷积。

我们只需各取两维在 \(\mathcal{\sqrt{n}}\) 内的贡献，再减去重复部分。这种做法也叫 \(\text{Dirichlet}\) 双曲线法，后面在杜教筛中会提到，它与数论分块仅仅相差一个分部求和。

多维数论分块

int H(int n)
{
	int ret=0;
	for (int l=1,r;l<=min(n,m);l=r+1)
	{
		r=min(n/(n/l),m/(m/l));
		ret+=(r-l+1)*(n/l)*(m/l);
	}
	return ret;
}

---

莫比乌斯反演

狄利克雷说：$ \mu \ast 1 = \varepsilon $，然后便有了莫比乌斯反演。

若 \(f(n)=\sum_{d|n}g(d)\)，称 \(f(n)\) 是 \(g(n)\) 的莫比乌斯变换。

由 \(g=g \ast \varepsilon=g \ast 1 \ast \mu=f \ast \mu\) 知，\(g(n)=\sum_{d|n}\mu(d)f(\frac{n}{d})\)，称 \(g(n)\) 是 \(f(n)\) 的莫比乌斯反演。

通常还是直接使用 \(\mu \ast 1 = \varepsilon\) 将 \([n=1]\) 转为 \(\sum_{d|n}\mu(d)\)，下面是一个例子。

\[\begin{aligned} \sum_{i=1}^n\sum_{j=1}^m[(i,j)=k]&=\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}[(i,j)=1]\\ &=\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}\sum_{d|(i,j)}\mu(d)\\ &=\sum_{d=1}^{\min(\lfloor\frac{n}{k}\rfloor,\lfloor\frac{m}{k}\rfloor)}\mu(d)\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}[d|i][d|j]\\ &=\sum_{d=1}^{\min(\lfloor\frac{n}{k}\rfloor,\lfloor\frac{m}{k}\rfloor)}\mu(d)\lfloor\frac{\lfloor\frac{n}{k}\rfloor}{d}\rfloor\lfloor\frac{\lfloor\frac{m}{k}\rfloor}{d}\rfloor \end{aligned} \]

预处理后便可 \(\mathcal{O}(\sqrt{n})\) 应答上式。

---

欧拉反演

狄利克雷又说：\(\mu \ast \text{id} = \varphi\)，便有了欧拉反演。

\[\mu \ast \text{id}=\varphi \\ \mu \ast 1 \ast \text{id}=\varphi \ast 1 \\ \text{id}=\varphi \ast 1 \\ n=\sum_{d|n}\varphi(n) \]

于是我们可以对一些 \(\gcd\) 相关的式子进行化简，下面是一个例子：

\[\begin{aligned} \sum_{i=1}^n\sum_{j=1}^m(i,j)&=\sum_{i=1}^n\sum_{j=1}^m\sum_{d|(i,j)}\varphi(d)\\ &=\sum_{d=1}^{\min(n,m)}\sum_{i=1}^n\sum_{j=1}^m[d|i][d|j]\varphi(d)\\ &=\sum_{d=1}^{\min(n,m)}\varphi(d)\lfloor\frac{n}{d}\rfloor\lfloor\frac{m}{d}\rfloor \end{aligned} \]

预处理后便可 \(\mathcal{O}(\sqrt{n})\) 应答上式。

---

常用结论

\[\lfloor\frac{\lfloor\frac{n}{i}\rfloor}{j}\rfloor=\lfloor\frac{n}{ij}\rfloor\ \ \ (n,i,j \in \mathbb{Z}^{+}) \]

\[d(ij)=\sum_{x|i}\sum_{y|j}[(x,y)=1] \]

\[\ln(n+1)-\ln{n} < \frac{1}{n} < \ln{n}-\ln(n-1) \]

\[\mathcal{O}(\sum_{i=1}^{n}\frac{n}{i})=\mathcal{O}(n \ln{n}) \]

---

杜教筛

杜教筛、PN 筛、Min_25 筛、洲阁筛均用于筛出一些复杂的数论函数。

对已知块筛的函数 \(f,g\)，杜教筛可以在 \(\mathcal{O}(n^{\frac{2}{3}})\) 时间内得到 \(f / g\) 的块筛。

如果你是第一次接触杜教筛，恐怕你也不知道块筛是什么，我想我们还是有必要进行一些前置知识的介绍。

整除集合

对一个正整数 \(n\)，我们称 \(D_n=\{\lfloor\frac{n}{m}\rfloor|m \in \mathbb{Z}^{+}\}\) 为它的整除集合，它的基数是 \(\mathcal{O}(\sqrt{n})\) 的。

块筛

对数论函数 \(f\)，它在所有 \(x \in D_n\) 位置上的前缀和称为它在 \(n\) 处的块筛，即 \(\{Sf(x)|x \in D_n\}\)。

有时我们只需要求某个 \(Sf(n)\)，但 \(n\) 可能会很大，以至于我们不能接受线性的时间复杂度。

而 \(Sf(n)\) 不能凭空得到，我们便退而求其次，试着求 \(f\) 的块筛，因为 \(Sf(n)\) 往往与 \(n\) 整除集合内其他位置的 \(Sf\) 存在递推关系。

Dirichlet 双曲线法

考虑这样一个问题：

已知 \(f,g\) 块筛，求 \(f \ast g\) 块筛。

\[\begin{aligned} S(f \ast g)(n)&=\sum_{k=1}^n(f \ast g)(k)\\ &=\sum_{k=1}^n\sum_{ij=k}f(i)g(j)\\ &=\sum_{ij \leq n}f(i)g(j)\\ &=\sum_{i \leq x}f(i)Sg(\lfloor\frac{n}{i}\rfloor)+\sum_{j \leq y}g(j)Sf(\lfloor\frac{n}{j}\rfloor)-Sf(x)Sg(y)\ \ \ (x,y>0 \and xy=n) \end{aligned} \]

最后一步就像求 \(\int_{0}^{+\infty}\frac{k}{x}dx\) 时，可以先对 \(\sqrt{k}\) 以内的部分积分，翻倍后减去 \(k\)（即那个边长为 \(\sqrt{k}\) 的正方形）一样。

我想这就是他叫“双曲线法”的原因。（感觉更像是二元的容斥）

取 \(x=y=\sqrt{n}\)，暴力求块筛，时间复杂度为：

\[\mathcal{O}(\sum_{k=1}^{\sqrt{n}}\sqrt{k})+\mathcal{O}(\sum_{k=1}^{\sqrt{n}}\sqrt{\frac{n}{k}})=\mathcal{O}(n^{\frac{3}{4}}) \]

若对 \(m\) 以内部分线性预处理，复杂度将变为 \(\mathcal{O}(m+\frac{n}{\sqrt{m}})\)。

故常取 \(m=n^{\frac{2}{3}}\)，使得总时间复杂度同样为 \(\mathcal{O}(n^{\frac{2}{3}})\)。

有一说一，不如数论分块。

但在另一个问题上，它将大显身手。

杜教筛

考虑这样一个问题：

已知 \(g,h\) 块筛，求 \(h / g\) 块筛。

注意前面我们得到了这样一个式子：

\[S(f \ast g)(n)=\sum_{i \leq \sqrt{n}}f(i)Sg(\lfloor\frac{n}{i}\rfloor)+\sum_{j \leq \sqrt{n}}g(j)Sf(\lfloor\frac{n}{j}\rfloor)-Sf(\sqrt{n})Sg(\sqrt{n}) \]

令 \(j=1\) 并移项可得：

\[g(1)Sf(n)=S(f \ast g)(n)-\sum_{i \leq \sqrt{n}}f(i)Sg(\lfloor\frac{n}{i}\rfloor)-\sum_{2 \leq j \leq \sqrt{n}}g(j)Sf(\lfloor\frac{n}{j}\rfloor)+Sf(\sqrt{n})Sg(\sqrt{n}) \]

从小到大枚举整除集合位置即可求得 \(f\) 的块筛，把 \(h\) 视为 \(f \ast g\)，即得到 \(h / g\) 的块筛。

本质还是对整除集合位置使用 \(\text{Dirichlet}\) 双曲线法，时间复杂度同上。

杜教筛模板

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=2e6,MAXN=N+7;
int tot,mu[MAXN],smu[MAXN],Smu[MAXN],p[MAXN];
bool vis[MAXN];

void init()
{
	mu[1]=1;
	for (int i=2;i<=N;i++)
	{
		if (!vis[i]) mu[i]=-1,p[++tot]=i;
		for (int j=1;(j<=tot)&&(i*p[j]<=N);j++)
		{
			vis[i*p[j]]=1;
			if (i%p[j]==0) break;
			mu[i*p[j]]=-mu[i];
		}
	}
	for (int i=1;i<=N;i++) smu[i]=smu[i-1]+mu[i];
}

inline ll Sg(int x) { return (x+1ll)*x>>1; }

void solve(int n)
{
	int sq=sqrt(n);
	for (int i=n/N+1;i<=sq;i++) Smu[i]=smu[n/i];
	for (int i=n/N;i;i--)
	{
		int m=sqrt(n/i),ret;
		ret=1+smu[m]*m-n/i;
		for (int j=2;j<=m;j++)
		{
			int x=i*j,y=n/i/j;
			ret-=y*mu[j];
			if (x>sq) ret-=smu[y];
			else ret-=Smu[x];
		}
		Smu[i]=ret;
	}
	ll Sphi=-Sg(sq)*smu[sq];
	for (int i=1;i<=sq;i++) Sphi+=1ll*i*Smu[i]+mu[i]*Sg(n/i);
	cout<<Sphi<<' '<<Smu[1]<<'\n';	
}

int main()
{
	init();
	int T;
	cin>>T;
	while (T--)
	{
		int x;
		cin>>x;
		solve(x);
	}
	return 0;
}

---

Dancing Links

考虑这样一个问题：

给定一个 \(N\) 行 \(M\) 列的矩阵，矩阵中每个元素要么是 \(1\)，要么是 \(0\)。

你需要在矩阵中挑选出若干行，使得对于矩阵的每一列 \(j\)，在你挑选的这些行中，有且仅有一行的第 \(j\) 个元素为 \(1\)。

我们容易得到如下所示的一个想法：

1. 枚举选择一行，并将其从矩阵中删除。（不重复决策）

2. 对上一步删除的行内的每个 \(1\)，将其所在列删除。（对应列为 \(1\) 的行已确定，可以剪枝）

3. 对上一步删除的列内的每个 \(1\)，将其所在行删除。（避免决策出现某列有多个 \(1\) 的情形）

4. 若操作后矩阵不为空，回到步骤 1。

5. 若操作后矩阵为空，但最后一次决策行中元素不全为 \(1\)，回溯并回到步骤 1。

6. 若操作后矩阵为空，且最后一次决策行中元素全为 \(1\)，则找到问题的一组解。

不难发现，每个 \(1\) 都是对问题的一个约束；但 \(0\) 只是对矩阵形式上的补足，缺乏实际意义。

所以在实际的精确覆盖问题中，\(0\) 的数量往往远多于 \(1\) 的数量。（以数独问题为例，一个决策中 \(0\) 的个数是数独边长的平方级，而 \(1\) 总是仅有四个）

如果直接使用二维数组模拟这个过程，每个 \(0\) 都要占据空间，空间复杂度通常很糟糕。

所以我们想到，可以用一个动态开点的数据结构，仅维护 \(1\) 的相关信息。

放心，这里并没有什么扫兴的根号和 \(\log\)，我们用链表就够了。（大概是高德纳最平易近人的想法）

对每个 \(1\)，它沿一个链表遍历过所有与它同列的 \(1\)，沿另一个链表遍历过所有与它同行的 \(1\)，也就是双向十字链表。（其实可以看成略去那些 \(0\) 之后的网格图，但首尾相接以便遍历）

最后加上一个重要剪枝：总是先解决 \(1\) 最少的状态。剩下的其实就是对上述流程的模拟了。

DLX 模板

#include <bits/stdc++.h>
using namespace std;

const int MAXN=250007;
int n,m,cnt,ans,seq[MAXN],dcs[MAXN],sta[MAXN],siz[MAXN],first[MAXN];
int U[MAXN],D[MAXN],L[MAXN],R[MAXN];

void build()
{
	for (int i=0;i<=m;i++)
	{
		L[i]=i-1,R[i]=i+1;
		U[i]=D[i]=i;
	}
	L[0]=m,R[m]=0,cnt=m;
}

void ins(int d,int s)
{
	cnt++,siz[s]++;
	dcs[cnt]=d,sta[cnt]=s;
	U[cnt]=s,D[cnt]=D[s];
	U[D[s]]=cnt,D[s]=cnt;
	if (!first[d]) first[d]=L[cnt]=R[cnt]=cnt;
	else
	{
		L[cnt]=first[d],R[cnt]=R[first[d]];
		L[R[first[d]]]=cnt,R[first[d]]=cnt;
	}
}

void remove(int s)
{
	L[R[s]]=L[s],R[L[s]]=R[s];
	for (int i=D[s];i!=s;i=D[i])
		for (int j=R[i];j!=i;j=R[j])
			U[D[j]]=U[j],D[U[j]]=D[j],siz[sta[j]]--;
}

void recover(int s)
{
	for (int i=U[s];i!=s;i=U[i])
		for (int j=L[i];j!=i;j=L[j])
			U[D[j]]=D[U[j]]=j,siz[sta[j]]++;
	L[R[s]]=R[L[s]]=s;
}

bool dance(int dep)
{
	if (!R[0])
	{
		ans=dep;
		return 1;
	}
	int s=R[0];
	for (int i=s;i!=0;i=R[i])
		if (siz[i]<siz[s]) s=i;
	remove(s);
	for (int i=D[s];i!=s;i=D[i])
	{
		seq[dep]=dcs[i];
		for (int j=R[i];j!=i;j=R[j])
			remove(sta[j]);
		if (dance(dep+1)) return 1;
		for (int j=L[i];j!=i;j=L[j])
			recover(sta[j]);
	}
	recover(s);
	return 0;
}

int main()
{
	cin>>n>>m;
	build();
	for (int i=1;i<=n;i++)
		for (int j=1;j<=m;j++)
		{
			int x;
			cin>>x;
			if (x) ins(i,j);
		}
	if (dance(1))
		for (int i=1;i<ans;i++)
			cout<<seq[i]<<' ';
	else puts("No Solution!");
	return 0;
}

我们对上面形式化的题意具体化：

1. 原来矩阵中的横行代表一个决策。

2. 原来矩阵中的竖列代表一个状态。

3. 问题等价于：选择部分决策，使其精确覆盖每个状态。（即每个状态对应一个决策）

这便是这类问题的共性，故我们将其统称为精确覆盖问题。

对于常见的数独游戏，实际上也能通过适当的建模将其转化为精确覆盖问题：

1. 三元组 \((行,列,数)\) 代表一个决策。

2. 二元组 \((行,数),(列,数),(宫,数),(行,列)\) 均代表状态，对应数独规则：
   每行中每个数都恰好出现一次。
   每列中每个数都恰好出现一次。
   每宫中每个数都恰好出现一次。
   每格中恰好填一个数。

口算一下，对于 \(9 \times 9\) 数独，决策数有 \(9^3=729\) 个，状态数有 \(4 \times 9^2=324\) 个。

而每个决策中，\(1\) 的数目固定为四个，\(0\) 的数目为 \(324-4=320\) 个，也应证了前面对 \(0/1\) 数量规模的分析。

至于时间复杂度，很抱歉，尽管它做了许多优化，这依然是一个指数级时间复杂度的算法。

但精确覆盖问题是一个 NPC 问题，这意味着除去对矩阵精心构造的情形（矩阵极小且 \(1\) 占比极大），DLX 基本是这个问题下的最优解。

---