矩阵学习笔记

矩阵乘法

为什么学？

xtx逼的！

能够套快速幂来加速递推（确信）。

---

基本性质

矩阵乘法的基本性质有：

1. 乘法结合律：$(AB)C=A(BC)$

2. 乘法左分配律：$(A+B)C=AC+BC$

3. 乘法右分配律：$C(A+B)=CA+CB$

4. 数乘结合性：$k(AB)=(kA)B=A(kB)$

5. 转置：$(AB)^T=B^TA^T$

---

交换律

咦？刚才是不是的基本性质把交换律打漏了？

并不是，这里是要来解释为什么矩阵乘法不满足交换律的。

交换律的不可行，我们可以轻松地用矩阵乘法的定义证明。

矩阵乘法要求左矩阵的列数与右矩阵的行数相同。

如矩阵 $A$ 为$a \times p$的矩阵，矩阵 $B$ 为 $p \times b$的矩阵，那么两个矩阵可以相乘，得到 $a \times b$ 的矩阵 $AB$ 。

如果将两个矩阵倒过来，就可能不满足矩阵乘法的要求。

故矩阵乘法不满足交换律，即：

$$AB \neq BA$$

既然聊到了 $AB\ BA$ 的问题，就多插一句。

矩阵乘法有如下规则：

矩阵 $A$ 左乘矩阵 $B$ ，得到矩阵 $AB$ ；

矩阵 $A$ 右乘矩阵 $B$ ，得到矩阵 $BA$ 。

由此可见，矩阵乘法严格来说应该从右往左运算。

---

结合律

这里给出我关于矩阵乘法满足结合律的一种理解：

矩阵乘法结合律的表达式如下：

$$(AB)C=A(BC)$$

因为矩阵乘法是一种映射（或者说函数）。

就可以通过我们熟悉的函数的方式理解。

定义：

$$A \ast X=f(X)$$

$$B \ast X=g(X)$$

根据前文所述，矩阵乘法是从右往左运算的，则有

$$(AB)=f(B)$$

$$(BC)=g(C)$$

再回来看最开始结合律的式子：

$$(AB)C=A(BC)$$

可以通过刚才的定义进行变形：

$$f(g(C))=f(g(C))$$

等式成立，原式证毕。

---

分配律

有了刚才迈出的第一步，接下来的工作就方便多了。

定义：

$$C \ast X=h(X)$$

$$(A+B) \ast X=F(X)=f(X)+g(X)$$

可得：

$$F(h(X)))=f(h(X))+g(h(X))$$

根据先前的定义可得：

$$(A+B)C=AC+BC$$

乘法左分配律得证。

乘法右分配律呢？同理？

显然不行。因为刚才的 $(A+B)$ 是外层函数，现在却变成了参数。

能zhua吗？

没有巧方法，那我们就回到矩阵乘法的定义来解决吧。

求证：$C(A+B)=CA+CB$ .

设C为 $m \times n$ 的矩阵，A为 $n \times p$ 的矩阵，B为 $n \times p$ 的矩阵。

先看等号左边：

$$(A+B)_{i,j}=A_{i,j}+B_{i,j}$$

$$C(A+B)_{i,j}=\sum_{k=1}^n C_{i,k} \cdot (A+B)_{k,j}=\sum_{k=1}^n C_{i,k} \cdot (A_{k,j}+B_{k,j})$$

再看等号右边：

$$CA_{i,j}=\sum_{k=1}^n C_{i,k} \cdot A_{k,j}$$

$$CB_{i,j}=\sum_{k=1}^n C_{i,k} \cdot B_{k,j}$$

$$(CA+CB)_{i,j}=\sum_{k=1}^n C_{i,k} \cdot (A_{k,j}+B_{k,j})$$

$$∴C(A+B)=CA+CB$$

证毕。

---

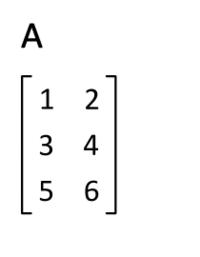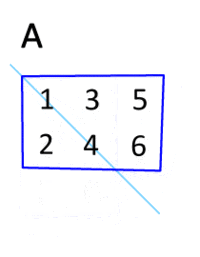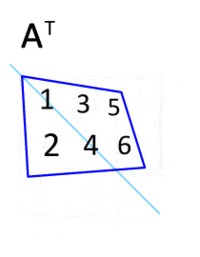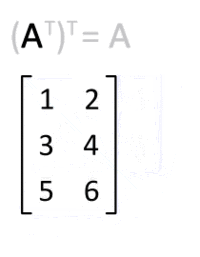
转置

即得易见平凡，仿照上例显然。留作习题答案略，读者自证不难。

反之亦然同理，推论自然成立，略去过程QED，由上可知证毕。

---

运用

---

矩阵快速幂

加法满足结合律，于是就产生了龟速乘。

乘法满足结合律，于是就产生了快速幂。

我们已经知道，矩阵乘法是一种满足结合律的运算。

所以，矩阵也可以像快速幂一样，通过二进制拆分加速求幂。

矩阵快速幂的时间复杂度是 $\mathcal{O} (n^3 \log T)$ 的，n为状态矩阵大小，T为递推次数，可以用于加速递推。

你怎么可以这么口胡过去啊喂！

行，那咱们来正经的。

设状态矩阵为一个 $1*n$ 的矩阵，如：

$$\begin{bmatrix} a_1\\ a_2\\ \vdots\\ a_n \end{bmatrix}$$

可以将其看作一个n维向量。

$∵$ n个n维向量（相互线性无关）能作为一个n维线性空间的基；

并且线性空间是关于向量加法与标量乘法运算封闭的向量集合。

$∴$ 我们能够通过这个n维向量映射到一个新的n维线性空间来完成一次线性递推。

而进行映射的方式便是矩阵乘法。

前面证明过，矩阵乘法满足结合律，能够用快速幂优化至 $\mathcal{O} (n^3 \log T)$ ，这就是矩阵加速递推的原理。

也因为矩阵乘法满足结合律，只要我们可以进行变量加与向量乘的运算，就能通过将这些操作相乘得到最后需要的转移矩阵。

当我们需要进行变量加时，直接增减转移矩阵上对应位置的数字即可，它相当于原矩阵的每个值在新矩阵对应位置上的权值。

如最经典的斐波那契数列：

$$\begin{bmatrix} 1 & 1\\ 1 & 0\\ \end{bmatrix} \begin{bmatrix} Fib_{i-1}\\ Fib_{i-2} \end{bmatrix}= \begin{bmatrix} Fib_i\\ Fib_{i-1} \end{bmatrix}$$

当我们需要进行常数乘时，也是同样的道理。

如对于：$f_i=2f_{i-2}$ 有：

$$\begin{bmatrix} 0 & 2\\ 1 & 0 \end{bmatrix} \begin{bmatrix} f_{i-1}\\ f_{i-2} \end{bmatrix}= \begin{bmatrix} f_i\\ f_{i-1} \end{bmatrix}$$

假如我们需要把两种运算结合起来，如： $f_i=2f_{i-1}+3f_{i-2}$

则可以把几次变化的矩阵相乘得到转移矩阵：

$$\begin{bmatrix} 2 & 1\\ 1 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 3 \end{bmatrix} \begin{bmatrix} f_{i-1}\\ f_{i-2} \end{bmatrix}= \begin{bmatrix} 2 & 3\\ 1 & 0 \end{bmatrix} \begin{bmatrix} f_{i-1}\\ f_{i-2} \end{bmatrix}= \begin{bmatrix} f_i\\ f_{i-1} \end{bmatrix}$$

这里只是展示把两种操作合成的过程，实际上我们可以通过观察系数更快地写出这个转移矩阵。

如果你的递推式还有常数加法运算呢？

把 $1$ 丢进初始的状态矩阵就好，之后与变量加流程相同，只不过这一位在状态矩阵中始终不变。

可见，矩阵乘法的初始状态矩阵就像一个背包，你需要在背包中准备好所有必需的原料，然后通过转移矩阵不停合成下一步所需的物品。

但是，背包太过沉重也会让你走得更慢。

注意到矩阵快速幂与快速幂时间复杂度的不同，实际上就是状态矩阵大小对矩阵乘法速度的影响。

立方级的增长使得我们不能忽视它的影响，能够通过状态矩阵其它部分得到的量就不应该被保存，防T。( 尽管我现在遇到最大的矩阵只有 $11*11$ )