初识主席树_Prefix XOR

主席树刚接触觉得超强，根本看不懂，看了几位dalao的代码后终于理解了主席树。

先看一道例题：传送门

题目大意：

假设我们预处理出了每个数满足条件的最右边界。

先考虑暴力做法，直接对x~y区间暴枚，求出答案。

主席树做法：设主席树的下标表示边界为i的信息。

网上找不到百度百科对主席树的定义，那我说说自己的理解。

主席树是一棵可持久化线段树，可以找出线段树的历史版本。

主席树的空间复杂度可以达到O((N+M)logN)(无修改的情况下)。

因为每一次修改至多修改logN个点。

有图为证：

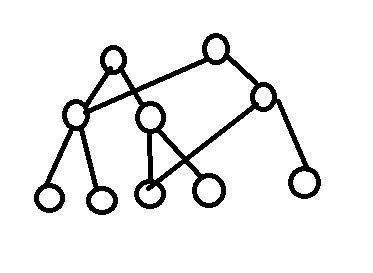
对于这道题，主席树维护的是边界为i的总和和总共有几个这样的点。

注意这里主席树的下标(i)是这个版本边界这个数为i。

主席树建树其实是对前缀1~i的建树。

因为你之前1~i-1建过树，你建的1~i版本是在1~i-1版本的基础上建立的。

边界就是你之前预处理出来的边界。

更新操作：

void updata(int l,int r,int &x,int y,long long v)
{
    T[++cnt]=T[y];x=cnt;//将当前版本与历史版本链接
    if(l==r){
        T[x].sum+=v;
        T[x].tot++;
        return ;
    }
    int mid=l+r>>1;
    if(mid>=v)updata(l,mid,T[x].l,T[y].l,v);//访问左节点
    else updata(mid+1,r,T[x].r,T[y].r,v);//访问右节点
    T[x].sum=T[T[x].l].sum+T[T[x].r].sum;
    T[x].tot=T[T[x].l].tot+T[T[x].r].tot;
}

 查询和：

long long Qsum(int l,int r,int x,int y,int ql,int qr)
{
    if(ql<=l&&qr>=r){
        return T[y].sum-T[x].sum;
    }//在查询区间内
    int mid=l+r>>1;
    long long ans=0;
    if(mid>=ql)ans+=Qsum(l,mid,T[x].l,T[y].l,ql,qr);
    if(mid<qr) ans+=Qsum(mid+1,r,T[x].r,T[y].r,ql,qr);
    return ans;
}

查询区间内有多少数：

long long Qcnt(int l,int r,int x,int y,int ql,int qr)
{
    if(ql<=l&&qr>=r){
        return T[y].tot-T[x].tot;
    }//在查询区间内
    int mid=l+r>>1;
    long long ans=0;
    if(mid>=ql)ans+=Qcnt(l,mid,T[x].l,T[y].l,ql,qr);
    if(mid<qr) ans+=Qcnt(mid+1,r,T[x].r,T[y].r,ql,qr);
    return ans;
}

All code：(被注释的部分是暴力代码)

#include <cstdio>
#include <algorithm>
using namespace std;

char tc()
{
    static char tr[1000000],*A=tr,*B=tr;
    return A==B&&(B=(A=tr)+fread(tr,1,1000000,stdin),A==B)?EOF:*A++;
}

int read()
{
    char c;while(c=tc(),c<'0'||c>'9');
    int x=c-'0';while(c=tc(),c>='0'&&c<='9')x=(x<<1)+(x<<3)+c-'0';
    return x;
}

const int MAXN=4*1e5;
long long N,Q,seed,a[MAXN+5],sum[MAXN+5],P[31][2];
long long nxt[MAXN+5];
struct node{
    int l,r;
    long long sum,tot;
}T[MAXN*40];
int root[MAXN+5],cnt;

void updata(int l,int r,int &x,int y,long long v)
{
    T[++cnt]=T[y];x=cnt;
    if(l==r){
        T[x].sum+=v;
        T[x].tot++;
        return ;
    }
    int mid=l+r>>1;
    if(mid>=v)updata(l,mid,T[x].l,T[y].l,v);
    else updata(mid+1,r,T[x].r,T[y].r,v);
    T[x].sum=T[T[x].l].sum+T[T[x].r].sum;
    T[x].tot=T[T[x].l].tot+T[T[x].r].tot;
}

long long Qsum(int l,int r,int x,int y,int ql,int qr)
{
    if(ql<=l&&qr>=r){
        return T[y].sum-T[x].sum;
    }
    int mid=l+r>>1;
    long long ans=0;
    if(mid>=ql)ans+=Qsum(l,mid,T[x].l,T[y].l,ql,qr);
    if(mid<qr) ans+=Qsum(mid+1,r,T[x].r,T[y].r,ql,qr);
    return ans;
}

long long Qcnt(int l,int r,int x,int y,int ql,int qr)
{
    if(ql<=l&&qr>=r){
        return T[y].tot-T[x].tot;
    }
    int mid=l+r>>1;
    long long ans=0;
    if(mid>=ql)ans+=Qcnt(l,mid,T[x].l,T[y].l,ql,qr);
    if(mid<qr) ans+=Qcnt(mid+1,r,T[x].r,T[y].r,ql,qr);
    return ans;
}

int buf[90];
void printf(long long x)
{
    buf[0]=0;
    while(x)
        buf[++buf[0]]=x%10,x/=10;
    if(!buf[0])buf[0]=1,buf[1]=0;
    while(buf[0])
        putchar(buf[buf[0]--]+'0');
}

int main()
{
//    freopen("HJT.txt","r",stdin);
//    freopen("W.txt","w",stdout);
    N=read();seed=read();
    register int i,j;
        for(i=1;i<=N;i++)a[i]=read(),sum[i]=sum[i-1]^a[i];
        for(i=0;i<=30;i++)P[i][0]=P[i][1]=N+1;
        for(i=N;i>0;i--){
            nxt[i]=N+1;
                for(j=30;j>-1;j--)
                    nxt[i]=min(nxt[i],P[j][(sum[i-1]>>j&1)^1]);
            nxt[i]--;
                for(j=30;j>-1;j--)
                    if((sum[i-1]>>j&1)^(sum[i]>>j&1))
                        {P[j][(sum[i]>>j&1)^1]=i;break;}
        }
        /*for(int i=1;i<=N;i++){
            for(int j=i+1;j<=N;j++){
                if((sum[j]^sum[i-1])<(sum[j-1]^sum[i-1])){
                    nxt[i]=j-1;
                    break;
                }
            }
            if(!nxt[i])nxt[i]=N;
        }*/
        for(i=1;i<=N;i++)
            updata(1,N,root[i],root[i-1],nxt[i]);
    Q=read();
    long long ans=0,Qs,Qc,x,y;
        for(i=Q;i;i--){
            x=read(),y=read();
            x=(x+ans*seed)%N+1,y=(y+ans*seed)%N+1;
            if(x>y)swap(x,y);
            ans=0;
            Qs=Qsum(1,N,root[x-1],root[y],x,y);
            Qc=Qcnt(1,N,root[x-1],root[y],y+1,N)*y;
            ans=Qs+Qc+(y-x+1)-(x+y)*(y-x+1)/2;
            printf(ans);putchar('\n');
            /*    for(int j=x;j<=y;j++)
                    ans+=min(nxt[j],y)-j+1;
            printf("%d\n",ans);*/
        }
    return 0;
}