sigmoid激活函数
sigmoid激活函数
sigmoid函数
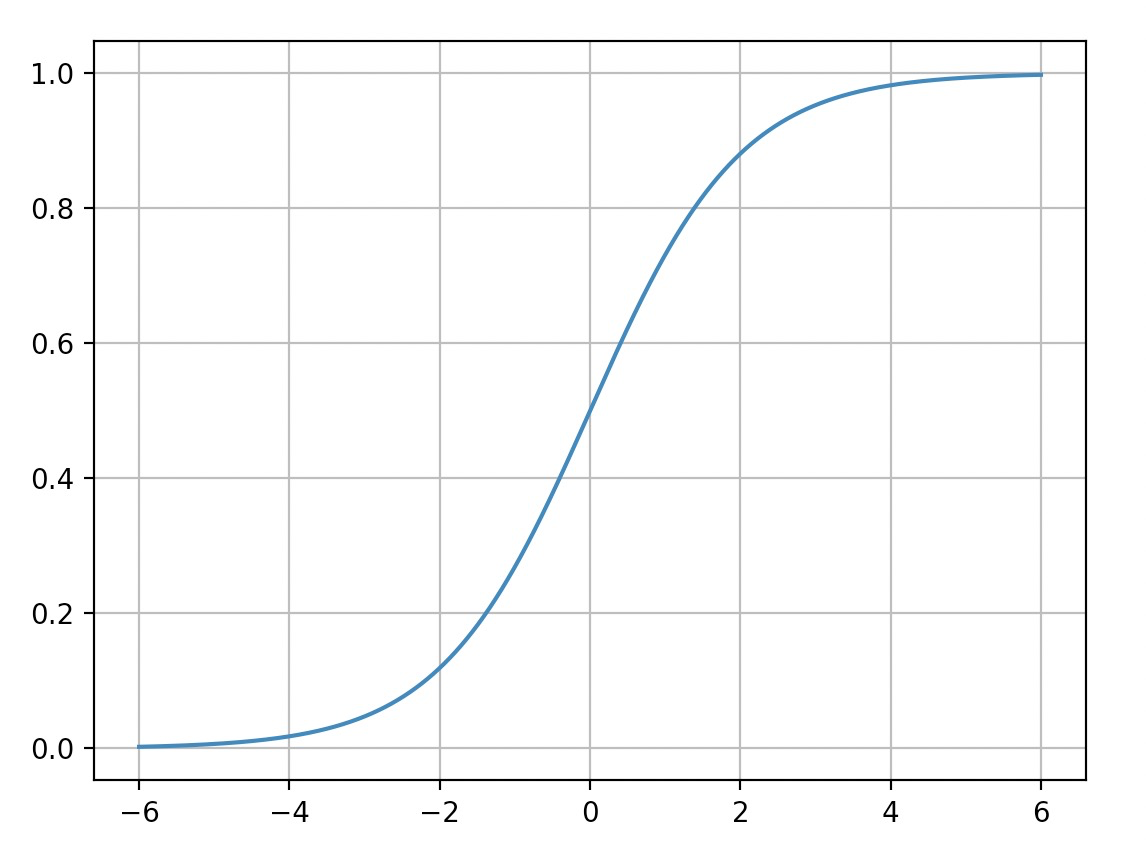
sigmoid激活函数是神经网络里最常见的激活函数之一，也叫逻辑斯蒂函数(Logistic Function)，常记作\(\sigma\)。
\[\sigma(x) = \frac{1}{1 + e ^ {-x}} = \frac{e^x}{e^x + 1}
\]
取值范围\([0,1]\)， 是关于\((0, 0.5)\)旋转对称的函数。其函数图像如下：
导数
\[\sigma'(x) = \frac{e^x}{(e^x+1)^2}=\frac{e^x}{e^x+1}\frac{1}{e^x+1}=\sigma(x)*(1-\sigma(x))
\]
导数的函数图像如下
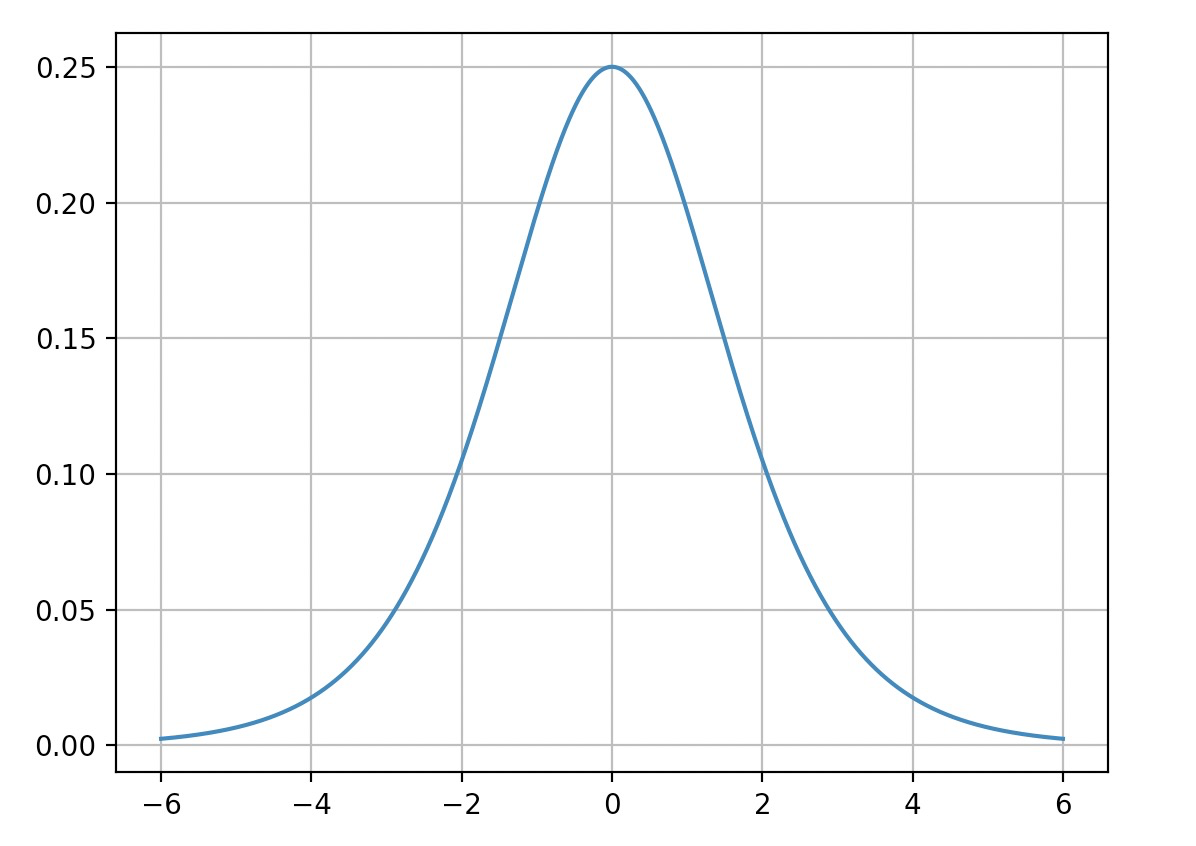
可以看到，其导数是关于y轴左右对称的。
sigmoid的缺点
从sigmoid函数的导数可以看出，当输入的x值绝对值比较大的时候，它的导数非常的小，从而导致梯度很小，更新缓慢。
优化
因为\(\sigma'(x)=\sigma(x)(1-\sigma(x))\)，所以在进行反向传播时，可以在前向计算时，存储其输出值\(\sigma(x)\)，然后在反向传播计算导数时，通过\(\sigma(x)(1-\sigma(x))\)来计算导数，从而提高效率。
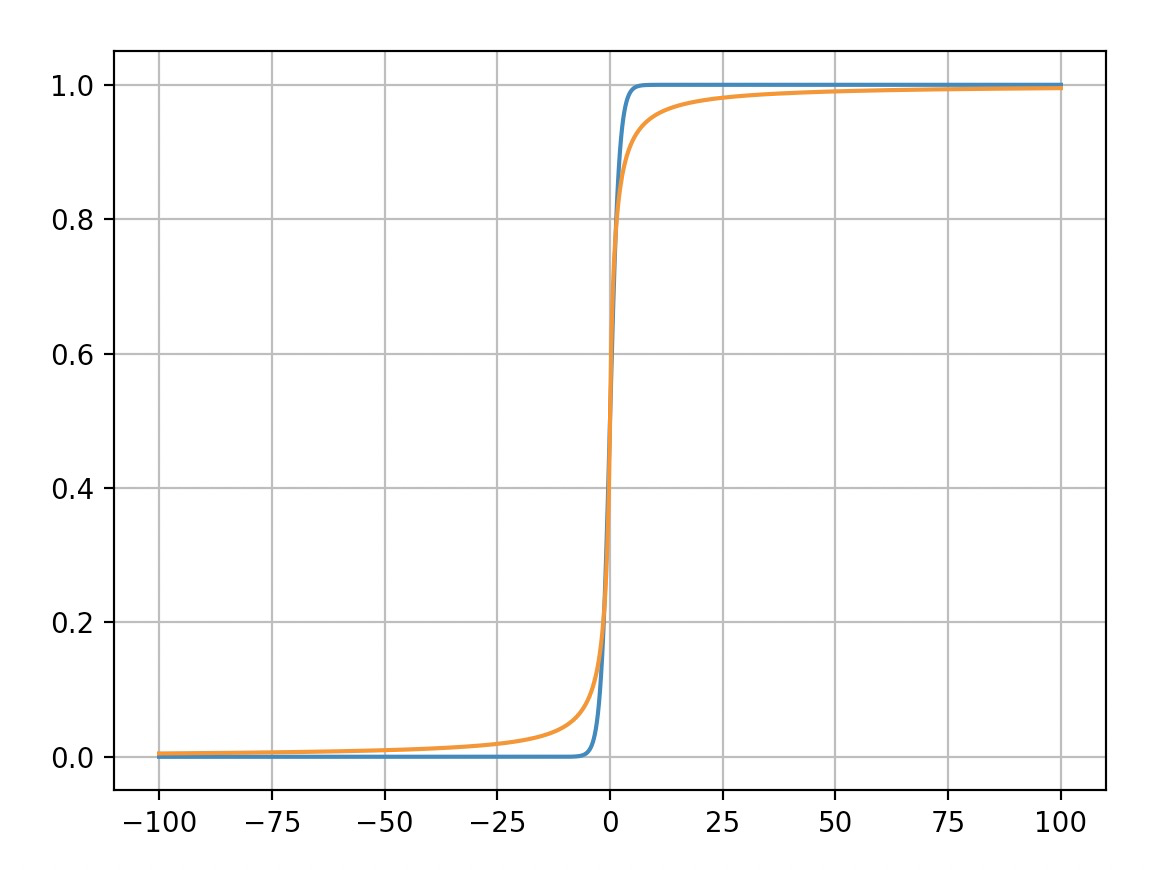
如果对精度要求不高的话，也可以通过其他函数对其进行逼近。比如
\[\sigmax(x)\approx \frac{x}{2(1+|x|)} + \frac{1}{2}
\]
