可持久化。
强制转发一波柱子恒的讲解,有些题题解我也有QAQ。
最近跑来打数据结构,于是我决定搞一发可持久化,然后发现……一发不可收啊……
对于可持久化数据结构,其最大的特征是“历史版本查询”,即可以回到某一次修改之前的状态,并继续操作;而这种“历史版本查询”会衍生出其他一些强大的操作。
今天,我们主要讲解可持久化线段树。其实,它的另外一个名字“主席树”似乎更加为人所知(主席%%%)。
主席树与普通的线段树相比,多出来的操作是在修改时复制修改的一条链,这个操作的过程大概长下面这样。
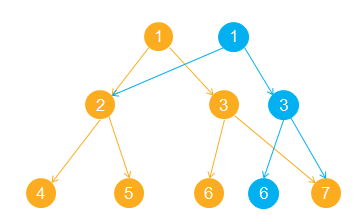
至于为什么要这样做……
对数据进行可持久化,一种朴素的想法是每一次修改新建一棵线段树,但是,时间复杂度和空间复杂度都是不允许我们做这样的操作的。
我们思考一下,每一次修改,只有一条链上的节点被修改,而其他的节点信息都没有变。因此,我们对这一次修改新建包括一个新根在内的logn个节点,其他的节点我们与上一课树共用。这样一来,我们既能保存之前的信息,又能进行修改操作。
主席树插入操作代码见下,有指针和数组2种版本:
指针版本:
1 void insert(node *&a,node *b,int l,int r,int pos) 2 { 3 a->cnt=b->cnt+1;//cnt表示这一棵树里的数据个数,a是新树,b是旧树,下同 4 int mi=(l+r)>>1; 5 if(l==r)return; 6 if(pos<=mi) 7 { 8 a->ch[1]=b->ch[1],a->ch[0]=newnode(); 9 insert(a->ch[0],b->ch[0],l,mi,pos); 10 } 11 else 12 { 13 a->ch[0]=b->ch[0],a->ch[1]=newnode(); 14 insert(a->ch[1],b->ch[1],mi+1,r,pos); 15 } 16 a->update(); 17 }
数组版本:
1 void insert(int rt1,int rt2,int l,int r,int pos) 2 { 3 if(l==r){cnt[rt1]=cnt[rt2]+1;return;}//cnt表示数据个数,rt1是新树,rt2是旧树 4 lc[rt1]=lc[rt2],rc[rt1]=rc[rt2]; 5 int mi=(l+r)>>1; 6 if(pos<=mi)lc[rt1]=++tot,insert(lc[rt1],lc[rt2],l,mi,pos); 7 else rc[rt1]=++tot,insert(rc[rt1],rc[rt2],mi+1,r,pos); 8 cnt[rt1]=cnt[lc[rt1]]+cnt[rc[rt1]]; 9 }
这一部分的基础题大概有cogs2554(http://cogs.pro/cogs/problem/problem.php?pid=2554 ),这就是一道主席树的入门水题,完全没有了解的同学可以通过这道题来入门。
可能有同学注意到了上面插入代码的cnt变量,它其实有大用:接下来,我们考虑用主席树进行一些更高级的操作:维护静态的区间第k大(小)值。
为什么主席树可以维护这个?
在对于一个序列查询k大(小)值时,我们把主席树建成权值线段树,每插入一个数就新建一个版本。这时,不难看出主席树具有区间可减性:
对于某一个区间【L,R】插入b个数以后区间中树的个数,减去【L,R】插入a-1个数以后区间中数的个数,
结果就是区间【a,b】中权值在【L,R】的数的个数。这样利用cnt变量不断查询,我们就可以找到某一个区间中第k大(小)的值
我们在代码实现时,只需要同时传入2个节点,并且比较区间数据个数之差与k的大小关系,进行移动即可
查询操作代码见下:
1 inline int query(int l,int r,int u,int v,int k) 2 { 3 node *a=root[u-1],*b=root[v]; 4 while(l<r) 5 { 6 int tmp=b->ch[0]->cnt-a->ch[0]->cnt,mi=(l+r)>>1; 7 if(tmp>=k)a=a->ch[0],b=b->ch[0],r=mi; 8 else a=a->ch[1],b=b->ch[1],k-=tmp,l=mi+1; 9 } 10 return r; 11 }
但是要注意,主席树在不做额外处理时只能查询静态的区间k大(小)值。
接下来,我们就考虑动态区间k小值。如果我们要对区间进行修改的话,一个简单的主席树已经无法实现了。
如果对原来的节点直接修改的话,会造成不可名状的运行错误(有兴趣的同学可以结合上面插入代码想一想为什么),
空间和时间也无法接受(我们需要把后面所有树都更改一下),但我们在做树套树的时候,可以做类似的操作,那么主席树是不是应该也套些什么呢?
主席树上的点,储存的都是在一段权值区间内的数据个数,我们必须要维护数据个数才可以通过相减得到一段区间的权值线段树。
而现在有了修改,对于这个修改的维护,朴素的做法有2种:O(1)查询,O(n)维护(扫一遍),和O(n)查询(现场算)和O(1)维护。
这两种做法都不是很忧,所以我们考虑利用快捷维护前缀和的树状数组解决这个问题,即所谓“树状数组套主席树”
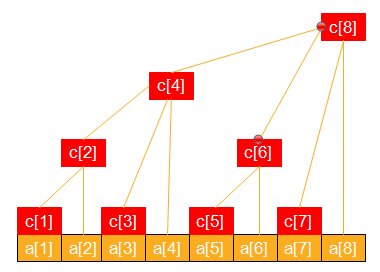
如图,图中c节点代表对应区间的线段树。比如,第8个点代表的线段树就是区间[1,8]的线段树,而第6个点代表的就是区间[5,6]的线段树。其他点同理。
在修改时,我们用树状数组找出需要修改的最多logn个节点,存起来,通过同时进行的一遍修改即可解决了。查询是类似的。
普通的树套树题都可以用树状数组套主席树来打,这里给出几道练习题:
bzoj3196 二逼平衡树 http://www.lydsy.com/JudgeOnline/problem.php?id=3196
bzoj1901 Zju2112 Dynamic Rankings(权限题)http://www.lydsy.com/JudgeOnline/problem.php?id=1901
cogs 257 动态排名系统 http://cogs.pro/cogs/problem/problem.php?pid=257
我cogs257 的代码 http://www.cnblogs.com/LadyLex/p/7275540.html
上面这些还没完。更强大的是,主席树不仅可以进行数列的维护,还可以对树上的数据进行操作和维护。
一般来说,我们有两种方法实现主席树上树:
一种是在父亲节点的基础上,在儿子节点新建树。这样可以维护出从某个点到根节点之间的数组,从而与LCA衍生出求树上某一条链的k值问题(或其他问题)
一种是按照两个把树转化为序列的工具:dfs序和欧拉序来建树,从而解决问题。这样可以截出一棵子树的值,从而衍生出其他问题。
如果带修改的话,就无法用上面第一种方法了,但还是可以用dfs序转成序列,再用树状数组套主席树。插入在进栈点+1,出栈点-1。删除在进栈点-1,出栈点+1。
一些例题:
BZOJ3123[Sdoi2013]森林 http://www.lydsy.com/JudgeOnline/problem.php?id=3123
本题我的题解:http://www.cnblogs.com/LadyLex/p/7275793.html
BZOJ3551 [ONTAK2010]Peaks加强版 http://www.lydsy.com/JudgeOnline/problem.php?id=3551
原题没有题面(和bzoj3545是一样的,不过bzoj3545是权限题),可以看一下我题解里的题面(强行安利一波)http://www.cnblogs.com/LadyLex/p/7275821.html
(另外其实上面这道题的主要知识点不是主席树,是克鲁斯卡尔重构树233)
除了上面这些,主席树还可以处理一堆五花八门的问题,由于这是普及向讲解以及我懒癌发作233不再一一列举。
主席树是一种功能强大的数据结构,通过新建链以及共用子节点的巧妙操作,不仅可以记录历史版本值,还可以支持很多其他操作。希望读完这篇博文的你可以有所收获!:)
另:接下来几天我还会补充可持久化平衡树(无旋Treap),可持久化Trie树以及可持久化并查集的讲解,敬请期待啦~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号