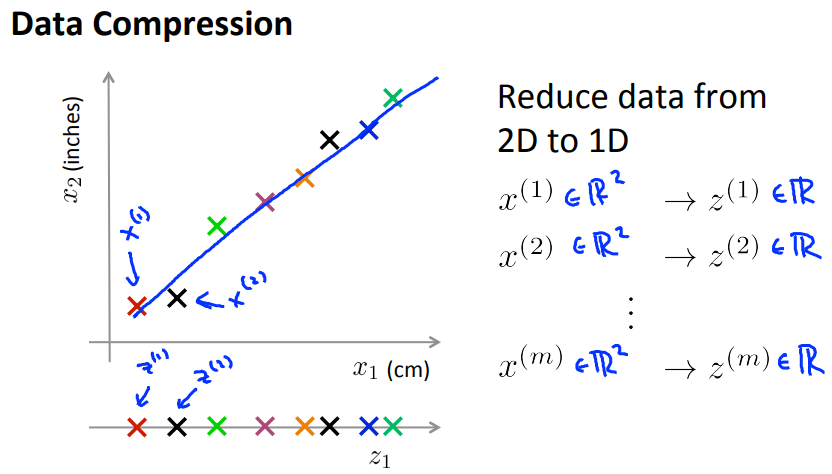
通过数据压缩(降维)可以减少特征数量,可以降低硬盘和内存的存储,加快算法的训练。
还可以把高维的数据压缩成二维或三维,这样方便做数据可视化。
数据压缩是通过相似或者相关度很高的特征来生成新的特征,减少特征数量。例如,上图x1是厘米,x2是英寸,这两个特征相关度很高,可以压缩成一个特征。
======================================
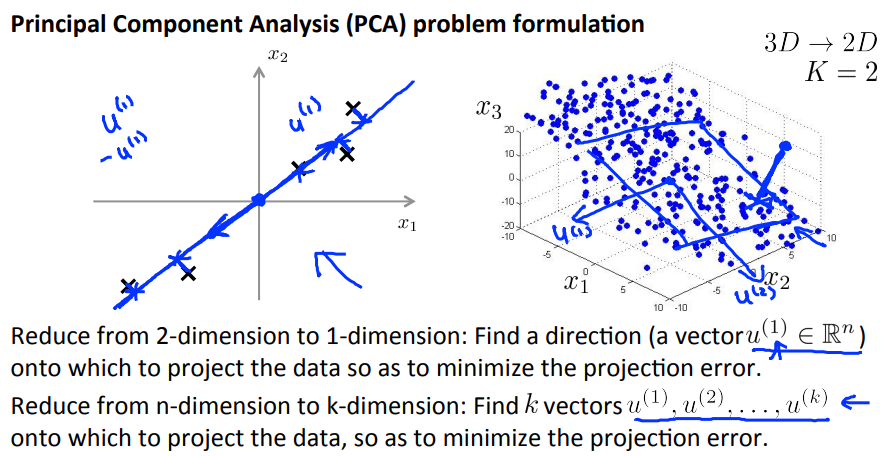
主成分分析(Principal Component Analysis, PCA)是常用的降维算法。
例如,要将二维数据压缩成一维数据,需要找到一个向量,使所有样本到该向量的投影误差(projection error)最小。
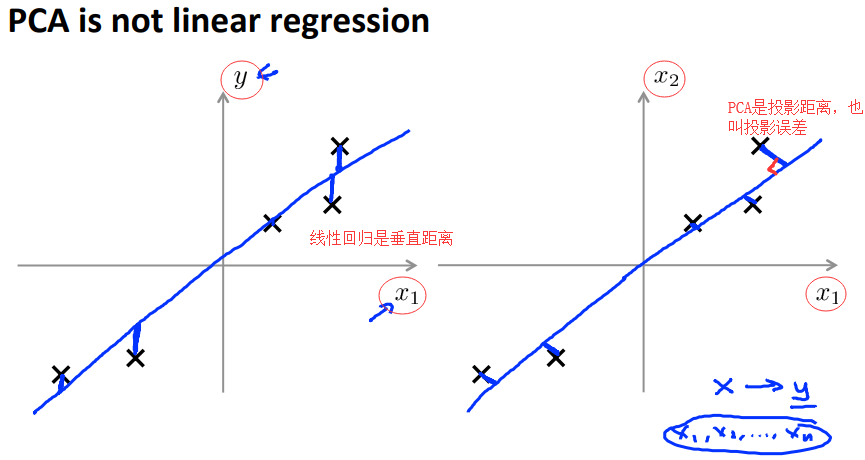
PCA不是线性回归,线性回归的差值是预测值和实际值的差,PCA的差值是样本到向量的投影误差。
线性回归需要用到标签,而PCA不需要用到标签。
======================================

在使用PCA算法前需要对数据进行预处理(每一个特征的均值要为0)。

首先需要计算协方差矩阵: sigma = (1/m) * X' * X
然后需要计算sigma的特征向量。 svd函数是奇异值分解(相关连接:https://www.cnblogs.com/pinard/p/6251584.html)
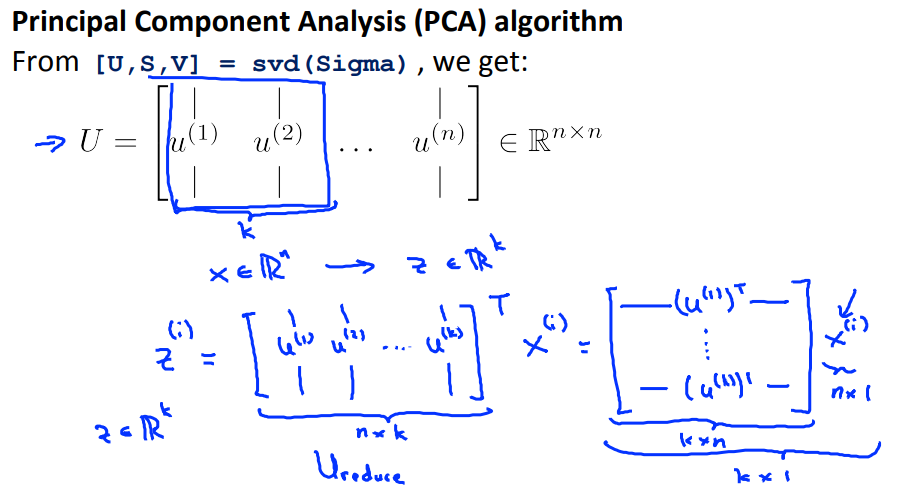

注意:每个特征的均值要为0,特征缩放是可选的。
svd返回的U是nxn维矩阵,前k列的矩阵称为Ureduce(nxk)。
Zi = Ureduce' * Xi
======================================
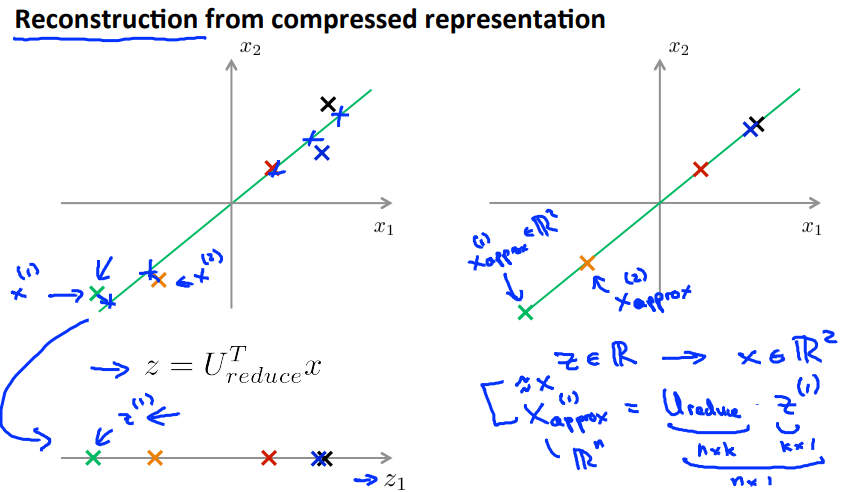
如何把压缩数据解压缩还原到原来的维度?
X(i)approx = Ureduce * Z(i)
======================================

如何选择合适的k值?即特征应该从n维降低到哪个维度?
1 - 投影误差的均方 / 总偏差 = 保留的样本差异(?% of variance is retained)
通常均方投影误差除以总偏差不大于0.01,0.05或0.10
在向别人描述降维结果的时候不是说从n维降低到了k维,而是说保留了多少百分比的样本差异。

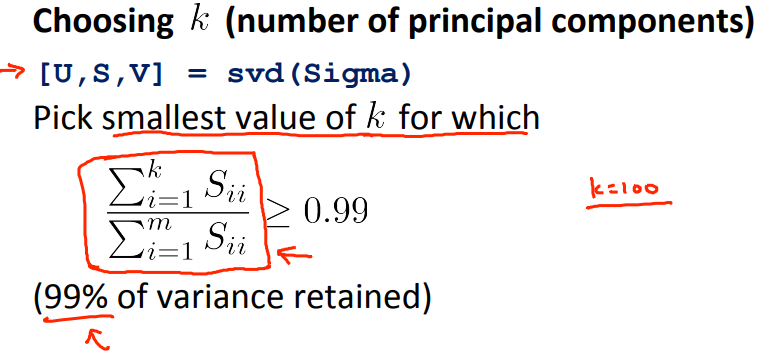
======================================



注意:PCA不适合用于处理过拟合。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号