机器学习之线性回归,预测函数,损失函数
机器学习最通俗的解释就是让机器学会决策。对于我们人来说,比如去菜市场里挑选芒果,从一堆芒果中拿出一个,根据果皮颜色、大小、软硬等属性或叫做特征,我们就会知道它甜还是不甜。类似的,机器学习就是把这些属性信息量化后输入计算机模型,从而让机器自动判断一个芒果是甜是酸,这实际上就是一个分类问题。
分类和回归是机器学习可以解决两大主要问题,从预测值的类型上看,连续变量预测的定量输出称为回归;离散变量预测的定性输出称为分类。例如:预测明天多少度,是一个回归任务;预测明天阴、晴、雨,就是一个分类任务。
线性回归(Linear Regression)
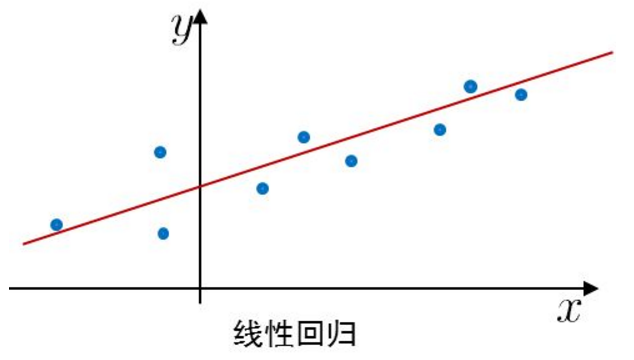
预测函数
![]()
![]()
损失函数
那么怎样评价它对于观测到的数据点拟合得好坏呢?所以需要对我们做出的假设hh进行评估,一般这个函数成为损失函数(loss function)
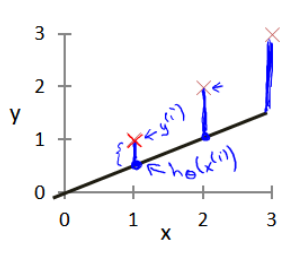
很直观的想法是希望预测值与实际值尽可能接近,即看预测值与实际值之间的均方误差是否最小,定义线性回归损失函数为
![]()
所以现在变成了一个优化问题,即找到要找到令损失函数J(θ)J(θ)最小的θθ。定义均方误差有着非常好的几何含义,对应常用的欧式距离(Euclidean distance),基于均方误差最小化进行模型求解的方法称为“最小二乘法”(least square method)。
原文:https://blog.csdn.net/jk123vip/article/details/80591619



 浙公网安备 33010602011771号
浙公网安备 33010602011771号