前缀和与差分

​ 前缀和就是一直累加即可，可以用于非常极速\(O(1)\)的区间查询。

​ 差分则是取每两个相邻数字的差值，可以用于非常急速\(O(1)\)的区间修改，当然仅限加减。如果是乘除什么的建议去线段树

​ 差分做一次前缀和可以得到原数组，原数组再做一次前缀和就是前缀和......算了文字太绕了看下面的LaTeX吧：

\(差分\underset{差分}{\overset{前缀和}{\rightleftharpoons}}原数组\underset{差分}{\overset{前缀和}{\rightleftharpoons}}前缀和\)

#include<iostream>
using namespace std;
const int N = 100010;
int a[N];
int s[N];//前缀和数组
int d[N];//差分数组
int main()
{
    int n;
    scanf("%d", &n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d", &a[i]);
        s[i] += s[i-1] + t;//上一个总和加现在的数得到当前总和
        
        d[i] = a[i] - a[i-1];//两个数之间的差值就是差分数组的目的
    }
    //对于查询而言，直接将查询区间头和尾的值相减即可。
    int l, r, v;
    while(1)
    {
        int command;
        scanf("%d%d%d%d", &command， &l, &r);/*假设1是前缀和的操作，2是修改区间的操作
        					两个修改的是两组不同数据，只是为了演示作用*/
        switch(command)
        {
            case 1:
                cout<<s[r] - s[l-1]<<endl; //查询从l到r的区间，因为包括了l，所以要往l-1位去找
                break;
            case 2:
                scanf("%d", &v);
                d[l]+=v;
                d[r+1]-=v;//因为区间修改从l到r，包括r，因此要往后一项去减去一个v
                //之所以要进行右端点减v，是因为修改的是一个区间，而差分修改一次会影响后面所有数据，所以在r+1的位置复原一次，保证后面区间不受影响。
                break;
        }
    }
    return 0;
}

二维差分

怎么说呢，放别人的图算了

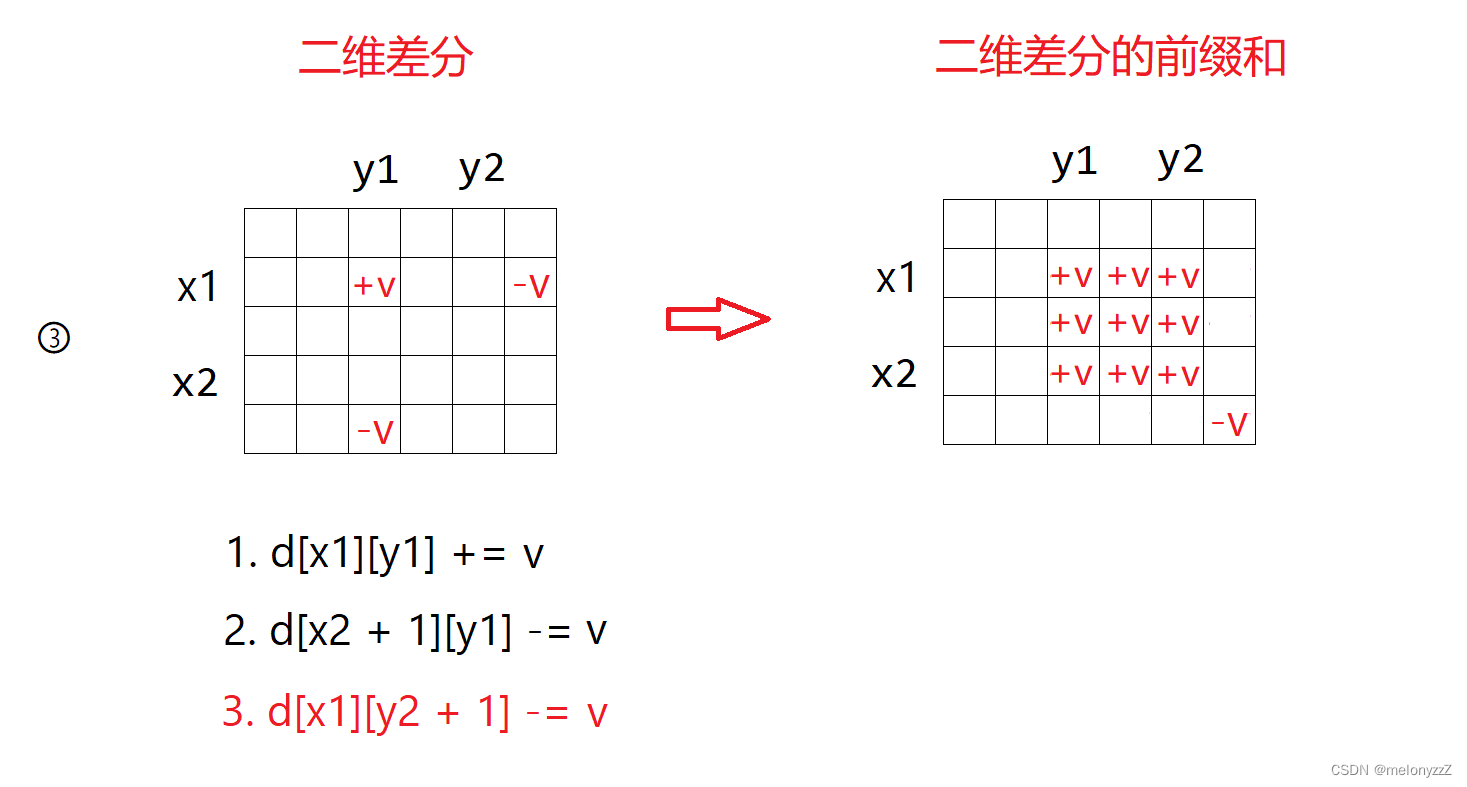
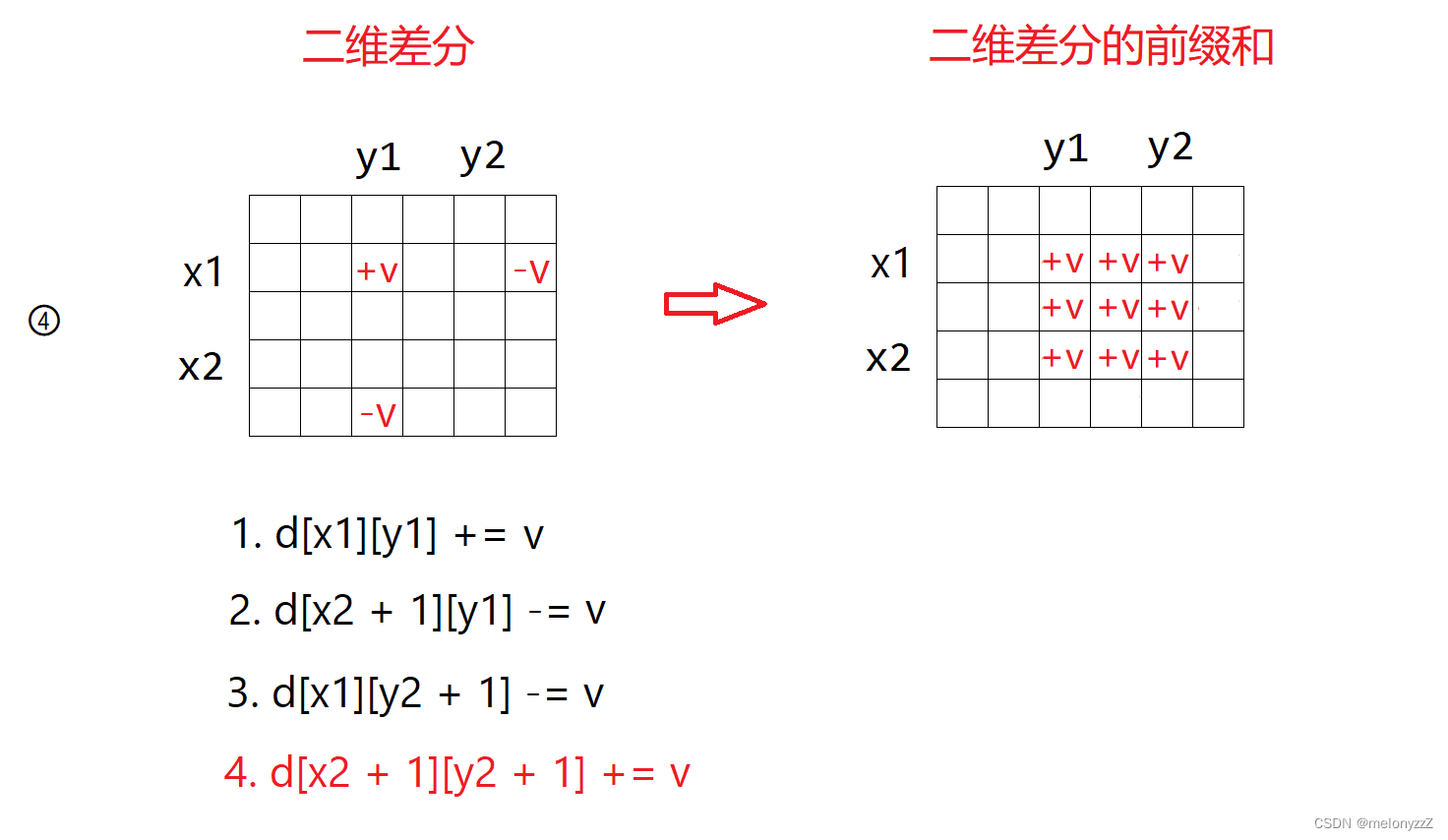
来源：https://blog.csdn.net/melonyzzZ/article/details/128448400

模板在此：

int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
b[x1][y1] ++;
b[x1][y2+1] --;
b[x2+1][y1] --;
b[x2+1][y2+1] ++;