动态字典树
#include <map> #include <set> #include <list> #include <cmath> #include <ctime> #include <deque> #include <stack> #include <queue> #include <cctype> #include <cstdio> #include <string> #include <vector> #include <climits> #include <cstdlib> #include <cstring> #include <iostream> #include <algorithm> #define LL long long #define PI 3.1415926535897932626 using namespace std; int gcd(int a, int b) {return a % b == 0 ? b : gcd(b, a % b);} struct node { node * child[2]; LL idx; int cnt; bool flag; }; LL ans,query; int N,M,cas; bool found; node * root; node* addnew() { node * u = (node*)malloc(sizeof(node)); for (int i = 0 ; i < 2; i++) u -> child[i] = NULL; u -> flag = false; u -> cnt = 0; return u; } void Insert(LL val,LL id) { node *u = root; for (LL i = 0 ; i <= 32 ; i++) { int tmp; if ((val & (1LL << (32 - i))) == 0) tmp = 0; else tmp = 1; if (u -> child[tmp] == NULL) u -> child[tmp] = addnew(); u = u -> child[tmp]; u -> cnt++; } u -> cnt++; } void del(LL val) { node * u = root; for (LL i = 0 ; i <= 32 ; i++) { int tmp; if ((val & (1LL << (32 - i))) == 0) tmp = 0; else tmp = 1; if (u -> child[tmp] == NULL) continue; u = u -> child[tmp]; u -> cnt--; } u -> cnt--; } void calcu(LL val,node * cur,int depth,LL sum) { if (depth >= 33) { ans = max(ans,sum); return; } int tmp; if (val & (1LL << (32 - depth))) tmp = 1; else tmp = 0; if (tmp == 1) { if (cur -> child[0] != NULL && cur -> child[0] -> cnt > 0) calcu(val,cur -> child[0],depth + 1,sum + (1LL << (32 - depth))); else if (cur -> child[1] != NULL && cur -> child[1] -> cnt > 0) calcu(val,cur -> child[1],depth + 1,sum); } else { if (cur -> child[1] != NULL && cur -> child[1] -> cnt > 0) calcu(val,cur -> child[1],depth + 1,sum + (1LL << (32 - depth))); else if (cur -> child[0] != NULL && cur -> child[0] -> cnt > 0 ) calcu(val,cur -> child[0],depth + 1,sum); } } int main() { cin >> N; root = addnew(); found = false; cas = N + 1; Insert(0,0); for (int i = 0 ; i < N ; i++) { char op[5]; cin >> op; if (op[0] == '+') { LL x; cin >> x; Insert(x,x); } else if (op[0] == '-') { LL x; cin >> x; del(x); } else { LL x; cin >> x; ans = 0; found = false; calcu(x,root,0,0); cout << ans << endl; } } return 0; }
Author has gone out of the stories about Vasiliy, so here is just a formal task description.
You are given q queries and a multiset A, initially containing only integer 0. There are three types of queries:
- "+ x" — add integer x to multiset A.
- "- x" — erase one occurrence of integer x from multiset A. It's guaranteed that at least one x is present in the multiset A before this query.
- "? x" — you are given integer x and need to compute the value
![]() , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.
, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer x and some integer y from the multiset A.
Multiset is a set, where equal elements are allowed.
The first line of the input contains a single integer q (1 ≤ q ≤ 200 000) — the number of queries Vasiliy has to perform.
Each of the following q lines of the input contains one of three characters '+', '-' or '?' and an integer xi (1 ≤ xi ≤ 109). It's guaranteed that there is at least one query of the third type.
Note, that the integer 0 will always be present in the set A.
For each query of the type '?' print one integer — the maximum value of bitwise exclusive OR (XOR) of integer xi and some integer from the multiset A.
10
+ 8
+ 9
+ 11
+ 6
+ 1
? 3
- 8
? 3
? 8
? 11
11
10
14
13
After first five operations multiset A contains integers 0, 8, 9, 11, 6 and 1.
The answer for the sixth query is integer 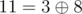 — maximum among integers
— maximum among integers 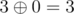 ,
, 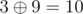 ,
, 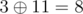 ,
, 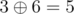 and
and 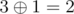 .
.


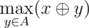 , i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer
, i.e. the maximum value of bitwise exclusive OR (also know as XOR) of integer 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号