[状压dp] Bzoj P2734 集合选数

Description

《集合论与图论》这门课程有一道作业题，要求同学们求出{1, 2, 3, 4, 5}的所有满足以 下条件的子集：若 x 在该子集中，则 2x 和 3x 不能在该子集中。同学们不喜欢这种具有枚举性 质的题目，于是把它变成了以下问题：对于任意一个正整数 n≤100000，如何求出{1, 2,..., n} 的满足上述约束条件的子集的个数（只需输出对 1,000,000,001 取模的结果），现在这个问题就 交给你了。 

Input

 只有一行，其中有一个正整数 n，30%的数据满足 n≤20。 

Output

 仅包含一个正整数，表示{1, 2,..., n}有多少个满足上述约束条件 的子集。 
 

Sample Input

4

Sample Output

8

【样例解释】
有8 个集合满足要求，分别是空集，{1}，{1，4}，{2}，{2，3}，{3}，{3，4}，{4}。

 

题解

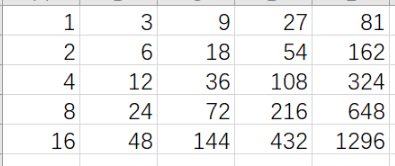
• 首先，可以写出一个这样的矩阵，然后发现不合法的数都在相邻的位置
• 然后n<=100000，其实最多就只有17列
• 设f[i][s]为做到第i行，第i行每个位置选数的状态
• 转移的话，枚举两行可能出现的状态，判断两个状态是否可行，也就是（s1&s2==0和s2&(s2>>1)==0）
• 最后，左上角的数不一定是1

代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int mo=1000000001;
long long ans=1;
int mi[20],n,a[20][20],s[20],f[20][2048];
bool bz[100005];
int work(int x)
{
    a[1][1]=x;
    for (int i=2;i<=18;i++)
        if (a[i-1][1]*2<=n)    a[i][1]=a[i-1][1]*2;
        else a[i][1]=n+1;
    for (int i=1;i<=18;i++)
        for (int j=2;j<=11;j++)
            if (a[i][j-1]*3<=n) a[i][j]=a[i][j-1]*3;
            else a[i][j]=n+1;
    memset(s,0,sizeof(s));
    memset(f,0,sizeof(f));
    f[0][0]=1;
    for (int i=1;i<=18;i++)
        for (int j=1;j<=11;j++)
            if (a[i][j]<=n)
            {
                s[i]+=mi[j-1];
                bz[a[i][j]]=1;
            }
    for (int i=0;i<18;i++)
            for (int j=0;j<=s[i];j++)
                if (f[i][j])
                    for (int k=0;k<=s[i+1];k++)
                        if (((j&k)==0)&&((k&(k>>1))==0))
                            f[i+1][k]=(f[i][j]+f[i+1][k])%mo;
    return f[18][0];

}
int main()
{
    scanf("%d",&n);
    mi[0]=1; for (int i=1;i<20;i++) mi[i]=mi[i-1]*2;
    for (int i=1;i<=n;i++) if (!bz[i]) ans=(ans*work(i))%mo;;
    printf("%d",ans);
    return 0;
}