[费用流]Bzoj P2424 订货

Description

某公司估计市场在第i个月对某产品的需求量为Ui，已知在第i月该产品的订货单价为di，上个月月底未销完的单位产品要付存贮费用m，假定第一月月初的库存量为零，第n月月底的库存量也为零，问如何安排这n个月订购计划，才能使成本最低？每月月初订购，订购后产品立即到货，进库并供应市场，于当月被售掉则不必付存贮费。假设仓库容量为S。

Input

第1行：n, m, S (0<=n<=50, 0<=m<=10, 0<=S<=10000)

第2行：U1 , U2 , ... , Ui , ... , Un (0<=Ui<=10000)

第3行：d1 , d2 , ..., di , ... , dn (0<=di<=100)

Output

只有1行，一个整数，代表最低成本

Sample Input

3 1 1000
2 4 8
1 2 4

Sample Output

34

 

解析

• 第一次打费用流，感觉不算很长吧
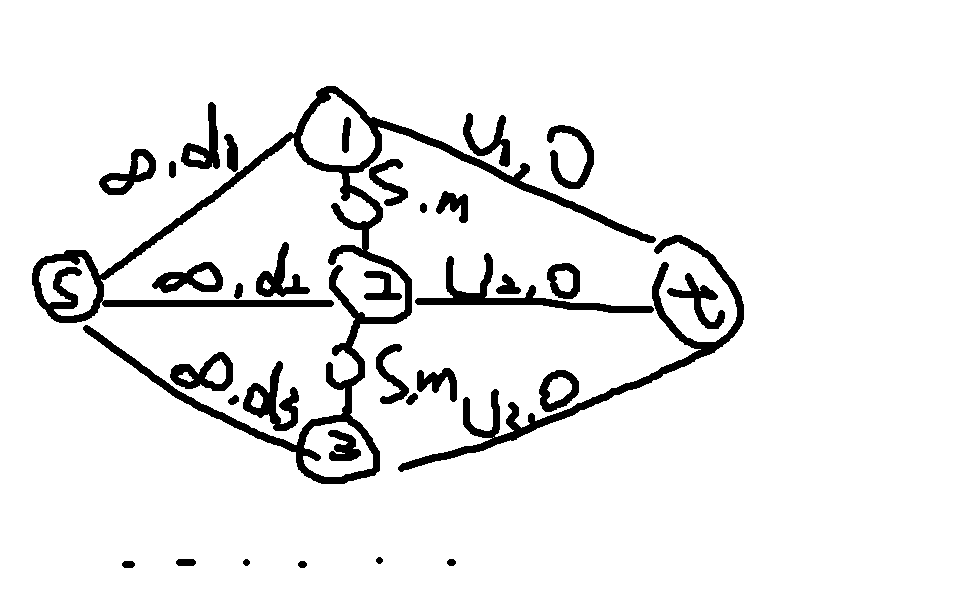
• 首先，我们可以每个月都建一个点(
• 那么，我们要考虑怎么将上个月多买的给留到下个月用
• 同上，我们也可以每个月都建一个仓库点，来转月
• 这样就形成了一个图了
• 然后就跑费用流
• （Tips：跑SPFA时要记录下路径，方便最后统计答案）
• 最后建图如下：
• 

代码

#include<cstdio>
#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
const int N=55;
const int inf=0x3f3f3f3f;
int n,m,S,cnt,last[N],t,dis[N],f[N],d[N],ans,s;
struct edge{int from,to,c,w,next;}e[N*N*2];
queue<int> Q;
void insert(int u,int v,int x,int y)
{
	e[++cnt].from=u; e[cnt].to=v; e[cnt].c=x; e[cnt].w=y; e[cnt].next=last[u]; last[u]=cnt;
	e[++cnt].from=v; e[cnt].to=u; e[cnt].c=0; e[cnt].w=-y; e[cnt].next=last[v]; last[v]=cnt;
}
bool spfa()
{
	for (int i=s;i<=t;i++) dis[i]=inf;
	dis[s]=0; Q.push(s); f[s]=1;
	while (!Q.empty())
	{
		int u=Q.front(); Q.pop();
		for (int i=last[u];i;i=e[i].next)
			if (e[i].c&&dis[u]+e[i].w<dis[e[i].to])
			{
				dis[e[i].to]=dis[u]+e[i].w;
				d[e[i].to]=i;
				if (!f[e[i].to]) f[e[i].to]=1,Q.push(e[i].to);
			}
		f[u]=0;
	}
	if (dis[t]<inf) return 1; else return 0;
}
void mcf()
{
	int mn=inf,x=t;
	while (d[x])
	{
		mn=min(mn,e[d[x]].c);
		x=e[d[x]].from;
	}
	ans+=dis[t]*mn;
	x=t;
	while (d[x])
	{
		e[d[x]].c-=mn;
		e[d[x]^1].c+=mn;
		x=e[d[x]].from;
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&S);
	s=0; t=n+1; cnt=1;
	int x;
	for (int i=1;i<=n;i++)
	{
		scanf("%d",&x);
		insert(i,t,x,0);
	}
	for (int i=1;i<=n;i++)
	{
		scanf("%d",&x);
		insert(s,i,inf,x);
	}
	for (int i=1;i<n;i++) insert(i,i+1,S,m);
	while (spfa()) mcf();
	printf("%d",ans);
	return 0;
}