[容斥] Luogu P5339 唱、跳、rap和篮球
题目描述
大中锋的学院要组织学生参观博物馆，要求学生们在博物馆中排成一队进行参观。他的同学可以分为四类：一部分最喜欢唱、一部分最喜欢跳、一部分最喜欢rap，还有一部分最喜欢篮球。如果队列中kk,k + 1k+1,k + 2k+2,k + 3k+3位置上的同学依次，最喜欢唱、最喜欢跳、最喜欢rap、最喜欢篮球，那么他们就会聚在一起讨论蔡徐坤。大中锋不希望这种事情发生，因为这会使得队伍显得很乱。大中锋想知道有多少种排队的方法，不会有学生聚在一起讨论蔡徐坤。两个学生队伍被认为是不同的，当且仅当两个队伍中至少有一个位置上的学生的喜好不同。由于合法的队伍可能会有很多种，种类数对998244353998244353取模。
题解
- 律师函警告（手动狗头）
- 设f(i)表示有i组人在鸡你太美的方案数，然后这样就可以进行容斥了
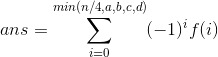
- 那么如何计算f(i)呢？如果视讨论cxk的组为一个元素，则一共有n−3∗i个元素
- 我们把问题转换成一个多重排列的方案数，求法： 现在有m个不同的元素，每个i元素有ai个，那么方案数为
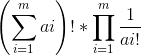
代码
1 #include <cstdio> 2 #include <iostream> 3 #define ll long long 4 #define N 2010 5 #define mo 998244353 6 using namespace std; 7 int n,a,b,c,d,lim; 8 ll fac[N],inv[N],f[N],res,ans; 9 int main() 10 { 11 scanf("%d%d%d%d%d",&n,&a,&b,&c,&d); 12 fac[0]=fac[1]=inv[0]=inv[1]=1; 13 for (int i=2;i<=n;i++) fac[i]=fac[i-1]*i%mo; 14 for (int i=2;i<=n;i++) inv[i]=(mo-mo/i)*inv[mo%i]%mo; 15 for (int i=2;i<=n;i++) inv[i]=inv[i]*inv[i-1]%mo; 16 lim=min(n>>2,min(min(a,b),min(c,d))); 17 for (int x=0,v;x<=lim;++x) 18 { 19 v=(x&1)?-1:1; 20 for (int i=0;i<=n;i++) f[i]=0; 21 for (int i=0;i<=a-x;i++) for (int j=0;j<=min(n-4*x-i,b-x);j++) f[i+j]=(f[i+j]+inv[i]*inv[j])%mo; 22 res=0; 23 for (int i=0;i<=c-x;i++) for (int j=0;j<=min(n-4*x-i,d-x);j++) res=(res+inv[i]*inv[j]%mo*f[n-4*x-i-j])%mo; 24 res=res*fac[n-3*x]%mo*inv[x]%mo,ans=(ans+v*res)%mo; 25 } 26 printf("%lld",(ans+mo)%mo); 27 }
