题解
- 这道题显然就是要求
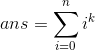
- 我们先考虑一下若何求一个i^k,对于第二类斯特林数我们知道Si,j表示为把i个有区别的球放入j个无区别的盒子的方案数(不存在空盒)
- 显然i^k也可以理解为将i个不同的盒子放入k个不同的球的方案数(允许空盒)
- 现在把允许空盒转换为每个盒子至少放一个球的方案数,对于存在k-j空盒的方案数就是 S[k][j]*C(i,j)*j!
- 这样的话我们就可以得出
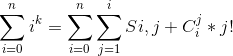
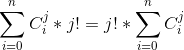
- 已知,
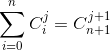
- 所以,
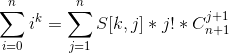
- 最后的话,这个东西怎么求呢,可以预处理斯特林数,再加个快速幂和防爆longlong的奇技淫巧就好了
代码
1 #include <cstdio>
2 #include <iostream>
3 #include <cstring>
4 #define ll long long
5 #define N 2010
6 using namespace std;
7 ll k,n,m,p,ans,s[N][N];
8 ll mul(ll x,ll y)
9 {
10 ll l=1e6,a1=x/l,a2=x%l,b1=y/l,b2=y%l;
11 return (a1*b1%p*l%p*l%p+a1*b2%p*l%p+b1*a2%p*l%p+a2*b2%p)%p;
12 }
13 ll ksm(ll a,ll b)
14 {
15 ll r=1;
16 for (;b;b>>=1,a=mul(a,a)) if (b&1) r=mul(r,a);
17 return r;
18 }
19 ll calc(ll n)
20 {
21 ll ans=0;
22 for (ll i=0;i<=k;i++)
23 {
24 ll r=s[k][i];
25 for (ll j=n+1;j>=n+1-i;j--) r=mul(r,(j%(i+1)==0)?j/(i+1):j);
26 ans=(ans+r)%p;
27 }
28 return ans;
29 }
30 int main()
31 {
32 scanf("%lld%lld%lld%lld",&k,&n,&m,&p),s[0][0]=1;
33 if (k>2000)
34 {
35 for (ll i=m;i<=n;i++) ans=(ans+ksm(i,k))%p;
36 printf("%lld",ans); return 0;
37 }
38 for (ll i=1;i<=k;i++) for (ll j=1;j<=i;j++) s[i][j]=(s[i-1][j-1]+j*s[i-1][j]%p+p)%p;
39 printf("%lld",(calc(n)-calc(m-1)+p)%p);
40 }
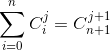
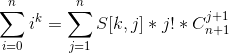


 浙公网安备 33010602011771号
浙公网安备 33010602011771号