【抄书笔记】《数据压缩导论》

第一章 引言

一. 性能测量需考虑的方面

  1. 算法复杂度
  2. 实现算法所需内存量
  3. 算法运行速度
  4. 压缩量
  5. 重构效果

二. 衡量压缩量的术语

  1. 压缩比
  2. 平均比特数 / rate 码率

三. 衡量重构效果的术语

  1. 失真
  2. 保真度
  3. 品质

四. 常见建模方法

  1. 预测元素值然后对残差编码
  2. 利用过去值预测当前值对预测误差编码（预测编码方案）
  3. 利用统计冗余
  4. 词典压缩方案解决重复冗余
  5. 查看符号群更容易看出数据中的结构或冗余
  6. 将数据分解为不同分量更便于利用数据中的结构，为每个分量应用一种合适模型

第二章 无损压缩的数学预备知识

自信息：\(i(A)=-log_b P(A)\)

  • 低概率事件的自信息量很高
  • 发生两个独立事件时获得的信息量 = 两个事件分布发生时获得的信息量之和
  • 信息的单位取决于对数的底 b。b=2，单位为 bit；b=e，单位为 nat 奈特，信息熵的对数单位；b=10，单位为 hartley 哈特莱。一般都假定底数为2。

熵：\(H=-\sum P(A_i)log_b P(A_i)\)

  • 信源的熵是对信源输出进行编码时所需二进制符号的平均个数
  • 无损压缩方案的最佳状态：对信源输出编码时，使用的平均比特数等于该信源的熵
  • 直观含义：每出现一个事件所给出的平均信息量

静态模型：模型的参数不随n发生变化

自适应模型：一个模型的参数随n发生变化以适应数据的变化特性

熵的估计值：实践中，数据的“实际”结构一般是不可知的，我们只能计算熵的估计值。了解数据中的结构，可以降低对熵的估计值，选择越来越大的数据块计算其概率，让数据块大小趋于无穷大，该概率值即趋近于熵。理论上考虑更多样本可以提取出信源的结构；实际中，需要一个合适的模型，因为通常观测一个很长的信源序列不现实。

信源模型：

  1. 物理模型
  2. 概率模型
    • 无知模型
    • 离散无记忆模型
    • Markov模型
  3. 组合信源模型

无知模型：信源的最简单统计模型就是假定信源生成的每个字母与其他字母无关，而且每个字母的出现概率相等。（1）放弃等概率假设，为符号集每个字母指定出现概率，可以计算信源熵（2）放弃独立性假设就要找出一种方法来描述数据序列中各元素之间的相互依赖关系。

马尔可夫模型：表示数据相关性的最常见方法之一。对于无损压缩中使用的模型，我们使用一种名为 离散时间马尔可夫链 的马尔可夫过程。

\(k\) 阶马尔可夫模型：知道过去 $k $ 个符号等于知道了该过程的整个历史，最常用1阶马尔可夫。

\[P(x_n|x_{n-1},...,x_{n-k})=P(x_n|x_{n-1},...,x_{n-k},...) \]

有限上下文模型：当代的文本压缩文献中，k 阶马尔可夫模型通常称为“有限上下文模型”（上下文就是马尔可夫过程中的状态）。上下文越长，预测值越好。但上下文的个数会随上下文长度呈指数增长。

前缀码：任何代码都不是另一代码的前缀。

第三章 霍夫曼编码

霍夫曼编码是一种前缀码，在给定模型（概率集）时是最优的。霍夫曼方法的基础是关于最优前缀码的两个观察结果：（1）在最优码中，符号的出现频率（出现概率）越高，其码字长度越短。（2）在最优码中，出现频率最低的两个符号有相同长度。霍夫曼过程向这两个观察结果增加了一条要求：对于最低概率的两个符号，其相应码字仅最后 1 比特不同。

霍夫曼编码过程就是每次选取概率最低的两个符号分别连接0和1，然后两符号合并，概率值相加得到新的符号继续参与符号集概率排序。

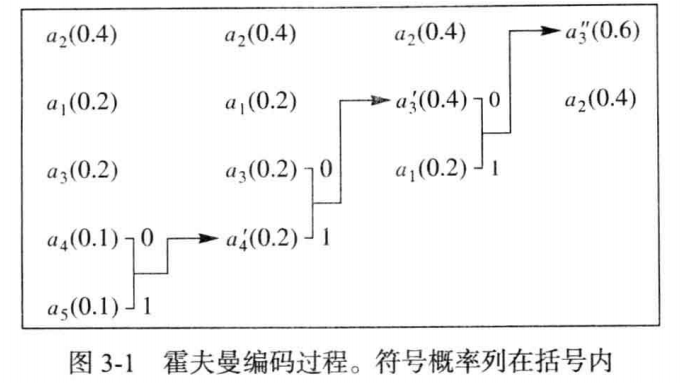
霍夫曼编码.png
**最小方差霍夫曼码**：每次将合并后的符号放在表中更高位置。
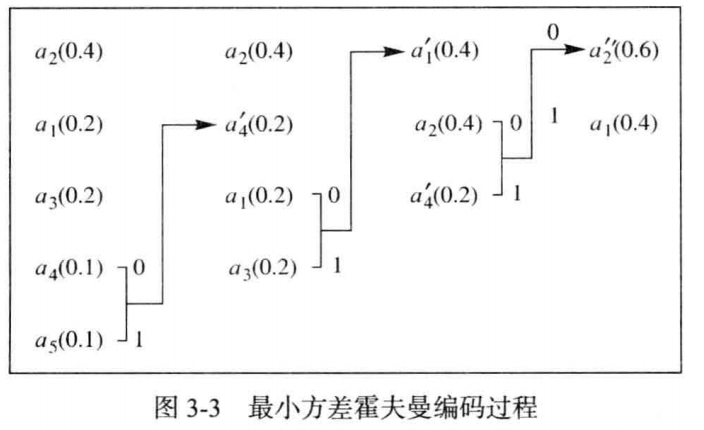
最小方差霍夫曼编码.png
两种编码方式的平均代码长度都是2.2比特/符号，但是码字长度的方差有很大不同。假如要以10000符号/秒的速度传送上述符号集中的符号，那要求传输容量为22000比特/秒。每一秒内，预计信道会不多不少正好接收22000比特。由于比特生成速率会在22000比特/秒上下变化，所以信源编码器的输出一般会放入一个缓冲区，来平滑比特生成速率的变化。但是，缓冲区大小有限，码字中的方差越大，缓冲区设计问题越困难。

范式霍夫曼码：一种高效存储霍夫曼码的方式。只需知道码字长度就可以获得霍夫曼编码。（1）根据字典顺序（2）短码字排在长码字之前

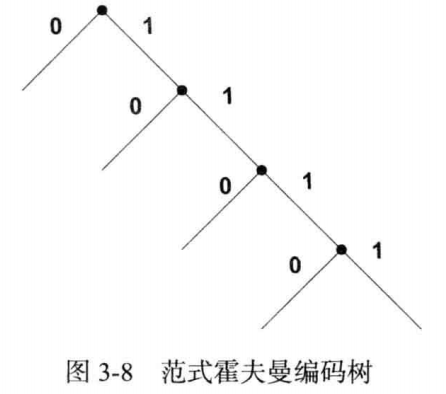
范式霍夫曼编码树.png
**霍夫曼码的实现**：如果速率是唯一考虑因素，可以使用查表法实现解码器，但对于解码器来说，表的大小必须为$2^N$，其中$N$是最长代码的长度。可能造成严重的存储浪费。随着最长码字长度的增加，浪费量也呈指数增长。另一种方法是将代码存储为二叉树，节约内存，但解码每个符号都要遍历这个树，计算效率低。大多数霍夫曼解码方法都会将基于表格的解码器和基于树的解码器结合，找到一个中间点。

自适应霍夫曼编码：如果没有信源序列的概率，根据编码过程中收集的符号统计信息来构造霍夫曼码。（1）1遍扫描。开始时认为等概率，根据前\(k(k=1,2,...)\)个符号统计重新产生码字并编码第\(k+1\)个字符（2）UNIX系统对程序的压缩：基于单词的自适应Huffman编码。

扩展的Huffman编码：考虑字母序列，而不是单个字母。理论上考虑更长的序列能提高编码性能，但字母表的指数增长使得这不现实，而且会有很多序列概率为0.

Golomb码：一类为整数设计的编码，假设整数值越大，概率越小。这类编码最简单的实现是一元码（正整数m的编码就是m个1后面加一个0），但实现过程简单。Golomb码将整数的一部分使用一元码，另一部分使用其他代码。

Rice码：一种自适应Golomb码。一个正整数序列被划分为包括J个整数的块，然后采取几种编码方式之一对每个块编码，这些编码方式大多为Golomb码。用每一种编码方式对块编码，选择比特数最少的方式，并在每个块的代码中附加一个字符，表示选择的编码方式。

CCSDS对无损压缩的建议：预处理器（建模）+二进制编码器（编码）。预处理器清除输入中的相关性，生成一个非负整数序列（序列性质：较小值出现概率大于较大值）。二进制编码器生成一个表示该整数序列的比特流。

预处理器功能：将序列中前一个值作为当前值的预测，生成误差序列，将误差序列映射为正整数序列，对正整数序列分段，每段进一步分块，随后使用选项之一对块进行编码。

第四章 算术编码

算术编码的适用场合：（1）小字母表：如二进制信源（2）概率分布不均衡（3）建模与编码分开

算术编码：从另一种角度对很长的信源符号序列进行有效编码。对整个序列产生唯一标识，标识是\([0,1)\)之间的一个数，而不用对该长度所有可能序列编码，用递归思想构造区间产生标识。

第八章 有损编码的数学基础

常用模型：（1）概率模型（2）线性模型（3）物理模型

无失真编码只适用于离散信源；对于连续信源，只能在失真受限制的情况下进行限失真编码（失真不超过给定条件下的编码）。

失真度量（\(\{x_n\}\)原始信源输出，\(\{y_n\}\)重构输出）：

  1. 平方误差 \(d(x,y)=(x-y)^2\)

  2. 绝对误差 \(d(x,y)=|x-y|\)

  3. 均方误差MSE

    \[\sigma_d ^2=\frac{1}{N}\sum_{n=1}^N(x_n-y_n)^2 \]

  4. 信噪比SNR \(SNR=\frac{power\{x{_n}\}}{power\{error\}}=\frac{\sigma_x^2}{\sigma_d^2}\)

  5. 分贝 \(SNR(db)=10log_{10}\frac{\sigma_x^2}{\sigma_d^2}\)

  6. 峰值信噪比PSNR

    \[PSNR(db)=10log_{10}\frac{x_{peak}^2}{\sigma_d^2} \]

    \[x_{peak}=max|x{_n}| \]

  7. 绝对最大误差 \(d_{\infty}=max|x_n-y_n|\)

一般认为峰值信噪比与图像质量近似成正比关系，但峰值信噪比度量与人的视觉感知不完全一致。用数学模型表示人类的感知机制是复杂困难的。

互信息：随机变量之间相互提供的信息量，自信息与条件自信息之间的差，互信息是对称的。

互信息定义：\(I(a_j;b_k)=I(a_j)-I(a_j|b_k)=I(b_k;a_j)=I(b_k)-I(b_k|a_j)\)，表示符号\(b_k\)为\(a_j\)提供的信息量，或符号\(a_j\)为\(b_k\)提供的信息量。

条件自信息：\(I(a_j|b_k)\)表示在发现信源编码器输出为\(b_k\)时，对应的信源发出符号\(a_j\)的不确定度。\(I(a_j|b_k)=-logP(a_j|b_k)\)。\(I(b_k|a_j)\)表示在信源发出符号为\(a_j\)而编码输出为\(b_k\)的不确定度。\(I(b_k|a_j)=-logP(b_k|a_j)\)。

平均互信息：\(I(X;Y)=\sum\sum P(a_j,b_k)I(a_j;b_k)\)表示随机变量Y对X提供的平均信息量

信息熵：随机变量本身所含的信息量

条件熵：即平均条件自信息。

\[H(X|Y)=\sum\sum P(a_j,b_k)I(a_j|b_k)=-\sum\sum P(a_j,b_k)logP(a_j|b_k) \]

联合熵：\(H(X,Y)=-\sum P(X,Y)log P(X,Y)\)

当且仅当X与Y独立，X与Y之间的平均互信息为0，\(H(X,Y)=H(X)+H(Y)\)

\(I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)=H(X)+H(Y)-H(X,Y)\)

率失真函数：在给定失真条件下，最起码要多大的码率，才能保证不超过允许的失真。即确定每个编码符号至少提供多少关于信源符号的信息量。即在一定失真条件下，平均互信息\(I(X;Y)\) 的最小值\(minI(X;Y)\)。

\(I(X;Y)=\sum\sum P(a_j,b_k)I(a_j;b_k)\)

\(P(a_j,b_k)=P(a_j)P(b_k|a_j)\)

\(I(a_j;b_k)=I(b_k;a_j)=I(b_k)-I(b_k|a_j)=-logP(b_k)+logP(b_k|a_j)=log\frac{P(b_k|a_j)}{P(b_k)}\)

\(I(X;Y)=\sum \sum P(a_j)P(b_k|a_j)log\frac{P(b_k|a_j)}{P(b_k)}\)

即互信息由 （1）信源符号概率\(P(a_j)\)（2）编码输出符号概率\(P(b_k)\)（3）已知信源符号出现的条件概率\(P(b_k|a_j)\)决定。

在确定信源的条件下，\(P(a_j)\)已知，选择编码方法，实际上是改变条件概率\(P(b_k|a_j)\)的分布来控制平均互信息量。

率失真理论：在允许一定失真\(D\)的情况下，信源输出的信息传输率可压缩到\(R(D)\)。

失真函数：定量的失真测度\(d(a_j,b_k)\)

平均失真：失真函数\(d(a_j,b_k)\)的数学期望。由条件概率\(P(b_k|a_j)\)控制。

\(D=\sum\sum P(a_j,b_k)d(a_j,b_k)=\sum \sum P(a_j)P(b_k|a_j)d(a_j,b_k)\)

信源编码器的目的：使编码后所需码率\(R\)尽量小，而\(R\)越小，引起的平均失真越大。给出一个限制值\(D^{\star}\)，在满足\(D \le D^{\star}\)的条件下，选择一种编码方法使得码率\(R\)尽可能小。必然存在一个条件概率\(P(b_k|a_j)\)使得\(D \le D^{\star}\)。记\(P_{D^{\star}}=P(D \le D^{\star})\)为满足条件的条件概率的集合，由于互信息\(I(X;Y)\)也受条件概率\(P(b_k|a_j)\)控制，可将率失真函数\(R(D)\)定义为：

\[R(D)=\min \limits_{P\in P_{D^{\star}}}I(X;Y) \]

率失真函数是在允许失真为\(D^{\star}\)的条件下，信源编码给出的平均互信息的下界，也是数据压缩的极限码率。在定义域内，\(R(D)\)是正的、连续的下凹函数，单调递减。

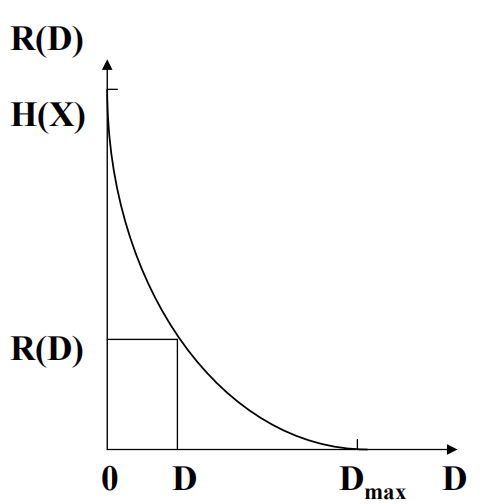
RD.png
**限失真信源编码定理（香农第三定理）**：说明最佳编码是存在的，而具体构造编码方法一无所知。一般只能从优化的思路去求最佳编码。实际上迄今尚无可实现的编码方法接近$R(D)$这个界。计算一个具体信源的$R(D)$也很困难，求解一个条件极小值问题，其解也是参数形式给出，其中起控制作用的变量只有$P(b_k)$。编码就是对$P(b_k)$的设计与实现，使码率接近$R(D)$。实际中一些编码方法不是直接设计$P(b_k)$而是从最后的码率来对$R(D)$函数做性能比较。

第九章 标量量化

量化：最简单、最重要的有失真编码

量化过程：（1）编码器映射：将一个范围内的值映射成一个区间，每个区间用唯一码字表示；有关信源的知识有助于选择合适的范围。（2）解码器映射：将码字映射成某个范围内的一个值；信源分布的知识有助于选择较好的近似。

量化问题：（1）输入：随机变量\(X\)，概率密度函数\(f_X(x)\)（2）输出：决策边界\(\{b_i\}\)，重构水平\(\{y_i\}\)（3）满足率失真准则，离散过程通常用连续分布近似，比如对像素差分用Laplacian建模（4）均方量化误差MSQE：

\[Q(x)=y_i,iff \ \ b_{i-1}<x\le b_i \]

\[\sigma_q^2=\int_{-\infty}^{\infty}(x-Q(x))^2f_Xdx=\sum_{i=1}^M \int_{b_{i-1}}^{b_i}(x-y_i)^2f_Xdx \]

量化器设计问题：\(M\)为量化器输出的字符数，则码率\(R=\lceil log_2 M\rceil\)。给定概率密度函数\(f_X(x)\)和\(M\)，求决策边界\(\{b_i\}\)和重构水平\(\{y_i\}\)，使得：MSQE最小。

均匀量化：所有区间大小相同，除了最外面两个区间。重构通常选择区间中点。

中升量化器：0不是一个输出水平。共有偶数个重构水平。

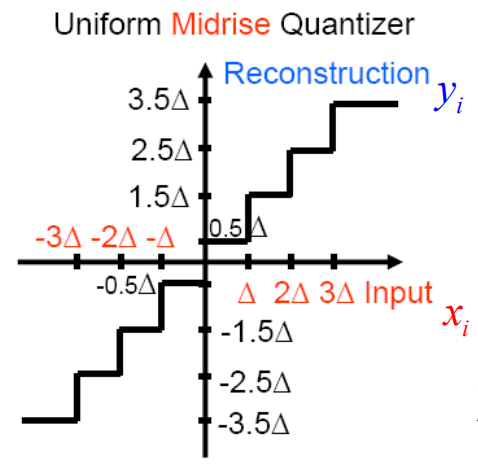
中升量化器.png
**中平量化器**：0是一个输出水平。共有奇数个重构水平。
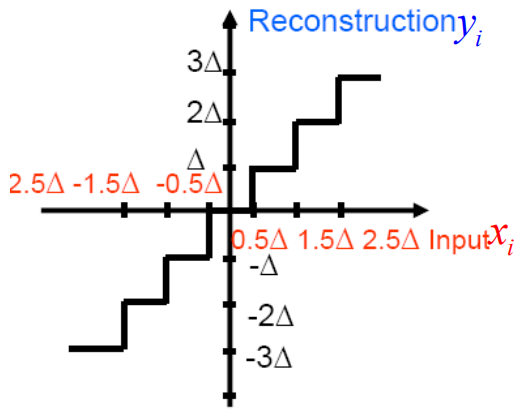
中平量化器.png
**自适应量化器**：不是静态方法，而是与真实数据相适应

前向自适应（离线）FAQ：将信源分块、分析块的统计特性、设置量化方案

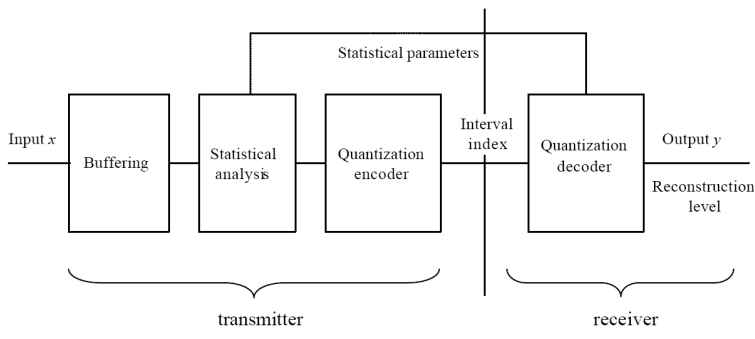
FAQ.png
**后向自适应（在线）BAQ**：基于量化器输出自适应
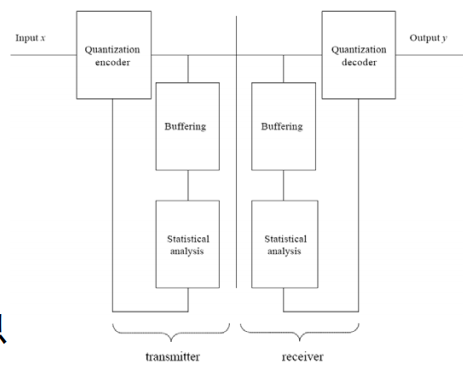
BAQ.png
**非均匀量化**：对给定$M$，为了减少MSQE，应在概率$f_X(x)$较大时缩小步长，在$f_X(x)$较小时增大步长。eg：Lloyd-Max量化器（pdf-最优量化器）

压扩量化（Companded Quantization, CQ）：将概率大的区域拉伸，概率小的区域压缩，用均匀量化器就可，对pdf变化不敏感

熵约束量化器：给定码率限制 \(H \le R_0\)，求\(\{b_i\}\)，\(y_i\)和二进制码字，使得：\(\sigma_q^2\)最小。用\(Lagrange\)费用函数：\(J(\lambda)=\sigma_q^2+\lambda H\)求解。费用函数太复杂，不能直接求解。用迭代法求解，ECSQ算法（二重循环）

嵌入式量化器：随着比特流的解码，渐进地精化重构数据。对低带宽连接有用。是JPEG2000的一个关键特征。

第十章 矢量量化

压缩符号串比压缩单个符号在理论上可产生更好的效果（比如图像和声音的相邻数据项都是相关的）。

矢量量化：量化时不是处理单个信源输出，而是一次处理一组符号（矢量）。矢量量化产生码书的方式，和对每个输入矢量查找与其最匹配码字的方式导致了各种矢量量化方法。

标量量化的不足之处：（1）所有码字分布在立方体内，对大多数分布都不是最有效的（2）量化区域通常是立方体（矢量量化是球形区域，体积相同时，最大粒状误差最小）

LBG算法：将Lloyd算法推广到矢量量化，亦称推广的Lloyd算法，类似k-means聚类。缺陷：编码复杂性高，需要全搜索；存储要求高，码书指数增长。

改进的矢量量化：（1）树结构矢量量化：搜索快，但存储量大（2）结构化的矢量量化：格型量化（3）网格编码矢量量化

树结构VQ：在码书组织中引入结构，快速决定哪个部分包含要输出的重构水平

格型量化：\(L\)维线性独立的\(L\)维矢量，每维赋予不同的权重，组成的\(L\)维矢量集合称为一个格。

TCQ量化：网格Trellis是一个有限状态机，随时间演化。

posted @ 2020-07-11 20:56  ColleenHL  阅读(625)  评论(0)  编辑  收藏  举报