[最优化理论与技术]无约束优化方法
无约束优化方法
概述
前言:无约束优化问题是实际问题中会碰到的问题。在解决约束优化问题的过程中会用到无约束优化问题的解法或思想。古典极值理论中,令一阶导为 0 ,要求二阶可微,然后判断海塞矩阵为正定才能求极小点,有理论意义而没有使用价值,实际中的多元函数很多不可微或不可求二阶导。但古典极值理论是无约束优化方法发展的基础。
无约束优化的数学模型
目前已研究出很多无约束优化方法,它们的主要不同点在于构造搜索方向上的差别。
-
解析法
直接应用目标函数极值条件来确定极值点。把求解目标函数极值的问题变成求解 \(\bigtriangledown f(x)=0\),一般求解比较困难,需要采用数值方法求解。与其用数值方法求解这个非线性方程组,还不如直接用数值法求解无约束极值问题。
-
数值法
数值法采用数学规划的思想,从起始点 \(x_k\) 开始沿搜索方向 \(d^0\) 进行搜索,确定最优步长 \(\alpha_k\) 使得函数值沿搜索方向下降最大。形成迭代的下降算法
\[x^{k+1}=x^k+\alpha_kd^k \]其中 \(d^k\) 是第 \(k+1\) 次搜索或迭代方向,称为搜索方向 (迭代方向)。
各种无约束优化方法的主要区别就在于确定搜索方向的方法不同。搜索方向的构成问题是无约束优化方法的关键。
无约束优化方法分类
根据构成搜索方向 \(d^k\) 所使用的信息性质,分为
- 利用目标函数的一阶或二阶导构造搜索方向的无约束优化方法 (间接法)。
- 最速下降法
- 牛顿法
- 共轭方向法
- 共轭梯度法
- 变尺度法
- 只用目标函数值的信息构造搜索方向的无约束优化方法 (直接法)。
- 坐标轮换法
- 鲍威尔方法
- 单型替换法
| 方法名称 | 迭代公式 |
|---|---|
| 一般迭代式 | $$x{k+1}=xk+\alpha_kd^k$$ |
| 最速下降法 | $$x{k+1}=xk-\alpha_k\bigtriangledown f(x_k)$$ |
| 牛顿法 | $$x{k+1}=xk-[\bigtriangledown 2f(x_k)]\bigtriangledown f(x_k)$$ |
| 阻尼牛顿法 | $$x{k+1}=xk-\alpha_k[\bigtriangledown 2f(x_k)]\bigtriangledown f(x_k)$$ |
| 共轭方向法 | \(x^{k+1}=x^{k}+\alpha_kd^k\); \(d_{k+1}=v_{k+1}+\sum_{i=0}^{k}\beta_{k+1,i} d_i\);\(\beta_{k+1,i}=-\frac{d_i^TGv_{k+1}}{d_i^TGd_i}\) |
| 共轭梯度法 | \(x^{k+1}=x^{k}+\alpha_kd^k\);\(d^{k+1}=-g_{k+1}+\beta_k d^k\);\(\beta_k =\frac{||g_{k+1}||^2}{||g_k||^2}\) |
最速下降法
最速下降法是一个古老的求解极值的方法,于 \(1847\) 年由柯西提出。
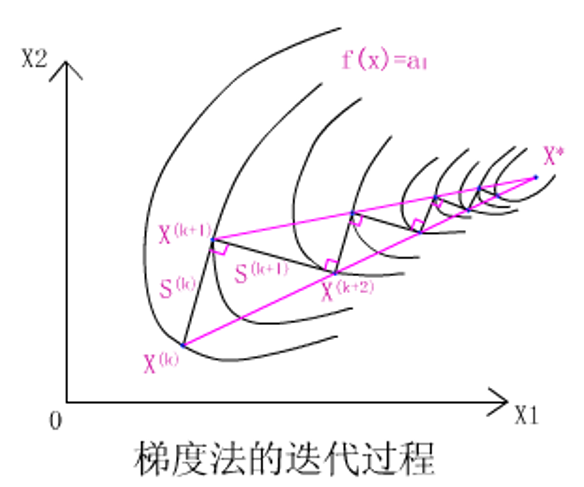
主要就是取负梯度方向为搜索方向。所以最速下降法又称 “梯度法”。
迭代算法为:
-
初始点 \(x^0\),\(k=0\),迭代阈值 \(\varepsilon\)
-
求 \(\bigtriangledown f(x^k)\),如果 \(||\bigtriangledown f(x^k)||\le \varepsilon\),输出 \(x^k\) 为最小值点,算法结束。否则继续。
-
确定搜索方向 \(d_k=-\bigtriangledown f(x^k)\)
-
确定一维搜索的最佳步长 \(\alpha_k\)
\[f(x^{k+1})=f[x^k-\alpha_k\bigtriangledown f(x^k)]=\min\limits _a f[x^k-\alpha\bigtriangledown f(x^k)]=\min\limits _a \phi(\alpha) \]\[\phi'(\alpha)=-\{\bigtriangledown f[x^k-\alpha_k\bigtriangledown f(x^k)]\}^T\bigtriangledown f(x^k)=0\\ \Rightarrow [\bigtriangledown f(x^{k+1})]^T\bigtriangledown f(x^k)=0 \]即相邻两迭代点上的函数梯度相互垂直,即相邻两个搜索方向互相垂直。
搜索路线呈“之”字锯齿形。
在接近极小点的位置,由于“之”字路线使得每次迭代行进的距离缩短,收敛速度减慢。主要是因为梯度是函数的局部性质,从整体看还是走了弯路,函数下降并不如人意。
小结:
- 理论明确,程序简单,对初始点要求不严格
- 因为梯度是函数的局部性质,所以整体收敛速度不快
- 搜索路线呈锯齿状,在远离极小点时逼近速度较快,接近极小点时速度较慢。
- 收敛速度与目标函数性质密切相关 。目标函数的等值线形成的椭圆簇越扁,迭代次数越多,搜索难以到达极小点;而同心圆,或椭圆簇对称轴,则一次搜索即可到达。(圆的切线垂直方向经过圆心,椭圆切线垂直方向不经过,除非在对称轴上的点)
最速下降法可以使目标函数在头几步下降特别快,所以可以与其他无约束优化方法配合使用。先最速下降求得较优初始点,再用其他收敛快的方法继续寻找极小点。
牛顿型方法
牛顿法
基本思想:用二次函数近似原目标函数,使用二次函数的极小点作为下一个迭代点。
泰勒展开:
设 \(x^{k+1}\) 为 \(\phi(x)\) 极小点,则 \(\bigtriangledown \phi(x^{k+1})=0\)
牛顿法能使二次型函数在有限次迭代内达到极小点,是二次收敛的。(对于二次函数,展开到二次项的泰勒展开式就是其本身,海塞矩阵是一个常数阵,一步找到极小点)
牛顿法纯粹基于极值的计算来确定极值点,没有包含下降方向搜索的思想,所以对于非二次函数,有时迭代后反而使函数值上升。
阻尼牛顿法
把 \(d^k=-[\bigtriangledown^2 f(x^k)]^{-1}\bigtriangledown f(x^k)\) 看作一个搜索方向,并称为 “牛顿方向”,再引入搜索方向里 “步长的” 概念。
- \(\alpha_k\) 是沿牛顿方向进行一维搜索的最佳步长,叫做 “阻尼因子”
- 原始牛顿法就是阻尼因子恒为1的情况
阻尼牛顿法每次都在牛顿方向上一维搜索,避免了迭代后数值上升的现象,又保留了牛顿法二次收敛的特性。
但是牛顿型方法每次都要计算海塞矩阵,再对海塞矩阵求逆,计算量巨大。条件苛刻,二次不可微的 \(f(x)\) 也不适用,若海塞矩阵是奇异矩阵不能求逆矩阵,也进行不下去,为了保证牛顿方向是下降方向,海塞矩阵的逆矩阵还必须正定。
共轭方向及共轭方向法
最速下降法存在“锯齿”现象,为了提高收敛速度,发展了一类共轭方向法,其搜索方向取共轭方向。
共轭的想法
最速下降法里,每一轮的梯度和上一轮的梯度正交,同一个方向重复走了多次,我们希望更新的搜索方向 \(d^{i}\) 与后一轮产生的误差 \(e^{i+1}=x^*-x^{i+1}\) 正交 (误差表示了参数最优点与当前点之间的距离)。
步长公式有了,但是 \(e^i\) 无法求。利用这种向量正交不可行。
采用另一种方法,令向量 \(d^{i}\) 与 向量 \(e^{i+1}\) 关于矩阵 \(G\) 共轭,\((d^i)^TGe^{i+1}=0\)。
- \(-G*e^i=-G(x^*-x^i)=Gx^i-Gx^*=r^i\)
- \(r^i=Gx^i\) 是当前点的负梯度,\(Gx^*=0\),最优点负梯度为0.
共轭方向
共轭概念是正交概念的推广,正交是共轭的特例。
正交:\((d^i)^Td^j=0\),则向量 \(d^i\) 向量 \(d^j\) 正交
共轭:\((d^i)^TGd^j=0 \ \ (i,j=0,1,...,m-1且i \ne j)\)。则向量 \(d^0,d^1,...,d^{m-1}\) 对 \(G\) 共轭 (它们是 \(G\) 的共轭方向),\(G\) 为 \(n \times n\) 对称正定矩阵。
当 \(G\) 为单位矩阵,则向量 \(d^0,d^1,...,d^{m-1}\) 互相正交。
共轭方向的性质:
-
若非零向量系 \(d^0,d^1,...,d^{m-1}\) 对 \(G\) 共轭,则这 \(m\) 个向量线性无关
-
在 \(n\) 维空间中互相共轭的非零向量数不超过 \(n\)
-
从任意初始点出发,顺次沿 \(n\) 个 \(G\) 的共轭方向 \(d^0,d^1,...,\) 进行一维搜索,最多经过 \(n\) 次迭代就可以找到二次函数的极小点。
-
说明这种迭代方法有二次收敛性
-
二次收敛性是若一算法对 \(Q\) 正定的二次目标函数
\(f(x)=ax^TQx+b^Tx+c\) 能在有限步内找出极小点来
-
共轭方向法
- 选定初始点 \(x^0\),下降方向 \(d^0\) 和收敛精度 \(\varepsilon\),设置 \(k=0\)
- 沿 \(d_k\) 方向一维搜索,得 \(x^{k+1}=x^{k}+\alpha_kd^k\)
- 判断 \(||\bigtriangledown f(x^{k+1})||< \varepsilon\),若满足,打印 \(x^{k+1}\),程序结束;否则转4
- 提供新的共轭方向 \(d^{k+1}\),使得 \((d^j)^T\times d^{k+1}=0\),\(k=k+1\),转2.
共轭方向的计算
\(Gram-Schmidt\) 向量组共轭化方法(向量组正交化方法的推广)
-
\(Gram-Schmidt\) 向量正交化方法:对第一个向量,保持不变;对第二个向量,去掉其中和第一个向量共线部分;...;对第 \(N\) 个向量,去掉其中和第 \(1,2,...,(N-1)\) 个向量共线的部分
-
对每一个向量做转换
\[d_{k}=v_{k}+\sum_{i=1}^{k-1}\beta_{k,i}d_i \]其中 \(\beta\) 表示向量被去掉的分量,利用向量之间共轭正交求 \(\beta\).
\[\begin{align*} d_l^TGd_k&=0,(l=1,2,...,k-1)\\ d_l^TGd_k&=d_l^TG(v_{k}+\sum_{i=1}^{k-1}\beta_{k,i}d_i)\\ &=d_l^TGv_{k}+d_l^TG\sum_{i=1}^{k-1}\beta_{k,i}d_i\\ &=d_l^TGv_{k}+d_l^TG\beta_{k,i}d_i\\&=0 \end{align*} \]则计算出
\[\beta_{k,i}=-\frac{d_l^TGv_k}{d_l^TGd_i} \]
共轭方向主要是针对二次函数的,也可用于一般非二次函数。因为非二次函数在极小点附近可用二次函数来近似:
- 二阶泰勒展开
- 海塞矩阵 \(G(x^*)\) 相当于二次函数中的矩阵 \(G\),但 \(x^*\) 未知。当迭代点 \(x^0\) 充分靠近 \(x^*\) ,可用 \(G(x^0)\) 构造共轭向量组
共轭梯度法
共轭方向与梯度的关系
考虑二次函数 \(f(x)=\frac{1}{2}x^TGx+b^Tx+c\)
沿 \(G\) 的某一共轭方向 \(d^k\) 做一维搜索,\(x^{k+1}=x^k+\alpha_kd^k\)
梯度 \(g_k=Gx^k+b\),则 \(g_{k+1}-g_k=G(x^{k+1}-x^k)=\alpha_kGd^k\)
假设 \(d^j\) 和 \(d^k\) 对 \(G\) 共轭,\((d^j)^TGd^k=0\),那么就有
- 这个式子表明,沿方向 \(d^k\) 进行一维搜索,终点 \(x^{k+1}\) 与始点 \(x^k\) 的梯度之差与方向 \(d^k\) 的共轭方向正交
- 共轭梯度法不用计算矩阵 \(G\) 就可求共轭方向
共轭方向的递推公式
共轭梯度法算法流程
- 选定初始点 \(x^0\),下降方向 \(d^0\) 和收敛精度 \(\varepsilon\),设置 \(k=0\)
- 沿 \(d_k\) 方向一维搜索,得 \(x^{k+1}=x^{k}+\alpha_kd^k\)
- 判断 \(||g_{k+1}||=||\bigtriangledown f(x^{k+1})||< \varepsilon\),若满足,打印 \(x^{k+1}\),程序结束;否则转4
- 计算共轭方向 \(d^{k+1}=-g_{k+1}+\beta_k d^k\),\(k=k+1\),转2.
变尺度法
梯度法构造简单,只用到一阶偏导数,计算量小,但只在开始几次迭代式函数值下降很快,迭代点接近 \(x^*\) 时,收敛非常慢;牛顿法收敛快,但要计算二阶偏导数及其逆矩阵,计算量太大。
变尺度法的基本思想
利用牛顿法的迭代公式,但不直接计算海塞矩阵 \(G^{-1}(x^k)\) 的逆,而是用一个对称正定矩阵 \(H_k\) 近似代替海塞矩阵的逆 \(G^{-1}(x^k)\),并且使 \(H_k\) 在迭代过程中不断改进,最后逼近 \(G^{-1}(x^k)\)。
迭代公式为
- \(H_k\) 就叫做尺度矩阵
- 关键就在于构造 $H_k $
尺度矩阵
通过尺度变换可以把函数的偏心程度降低到最低限度,尺度变换技巧能显著地改进几乎所有极小化方法的收敛性质。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号