机器学习线性模型

线性模型

目录

• 线性模型
  • 最小二乘法(LMS)
    • 数理推导
    • 几何意义推导
  • 极大似然 ( MLE )
  • Logistic回归(LR，逻辑回归模型，对数几率回归，二分类)
  • Softmax Regression ( Logistic 多分类引申 )
  • 岭回归 (Ridge Regression)
    • 岭回归
    • 梯度下降
    • 求解岭回归的损失函数
  • LASSO回归 ( Least Absolute Shrinkage and Selection Operator)
    • LASSO优化
  • 线性模型总结

最小二乘法(LMS)

数理推导

给定数据 \(D={(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(N)},y^{(N)})}\) ，\(h_{\theta}(x)=\theta^T x=\theta_0x_0+\theta_1x_1+...+\theta_nx_n=\theta_0+\theta_1x_1+...+\theta_nx_n\)

给定 \(N\) 组数据:

\[\theta_0+\theta_1x_1^{(1)}+\theta_2x_2^{(1)}+...+\theta_nx_n^{(1)}=y^{(1)} \]

\[\theta_0+\theta_1x_1^{(2)}+\theta_2x_2^{(2)}+...+\theta_nx_n^{(2)}=y^{(2)}\\ \vdots \]

\[\theta_0+\theta_1x_1^{(N)}+\theta_2x_2^{(N)}+...+\theta_nx_n^{(N)}=y^{(N)} \]

求解 \(\theta\)，使得输入 \(x\)，得到 \(\widehat{y}\)与\(y\)尽可能相似。求解线性方程组。

\[A =\left[\begin{matrix} 1& x_1^{(1)} & \dots & x_n^{(1)} \\ 1 & x_2^{(1)} & \dots & x_n^{(2)} \\ \vdots & \vdots & \quad & \vdots \\ 1 & x_1^{(N)} & \dots & x_n^{(N)} \end{matrix} \right] \]

\[\theta =\left[\begin{matrix}\theta_0 \\\theta_1 \\ \vdots \\ \theta_n\end{matrix}\right] \]

\[Y=\left[\begin{matrix}y^{(0)} \\y^{(1)} \\ \vdots \\ y^{(N)}\end{matrix}\right] \]

\(\Rightarrow 求解A \theta = Y\)，使得\(A \theta\)尽可能拟合\(Y\)

\[S=min_{\theta}||A\theta-Y||_2^2\quad (二范数的平方)\\=(A\theta-Y)^T(A\theta-Y)\\=(\theta^TA^T-Y^T)(A\theta-Y)\\=\theta^TA^TA \theta-\theta^TA^TY-Y^TA\theta+Y^TY\\=\theta^TA^TA \theta-2\theta^TA^TY+Y^TY \]

最优解即：

\[\frac{\partial S}{\partial \theta}=0 \Rightarrow \frac{\theta^TA^TA \theta-2\theta^TA^TY+Y^TY}{\partial \theta}=\frac{\partial (\theta^TA^TA \theta)}{\partial \theta}-2A^TY+0 \]

因为 \(\frac{d(u^Tv)}{dx}=\frac{du^T}{dx}v+\frac{dv^T}{dx}u\)

所以 \(\frac{d(x^Tx)}{dx}=\frac{dx^T}{dx}x+\frac{dx^T}{dx}x=2x\)

进一步 \(\frac{d(x^TBx)}{dx}=\frac{dx^T}{dx}Bx+\frac{dx^TB^T}{dx}x=Bx+B^Tx=(B+B^T)x\quad B是方阵\)

应用到方程中，将 \(A^TA\) 对应方阵 \(B\)，则 \(\frac{\partial S}{\partial \theta}=2A^TA\theta-2A^TY=0\quad \Rightarrow A^TA\theta = A^TY\)

\[\theta=(A^TA)^{-1}A^TY \]

• 数据较小时(不超百万)用最小二乘法代替梯度下降可以取得不错的结果。
• 求矩阵的逆是最消耗时间的
• 用梯度下降会存在收敛问题，步长\(\alpha\) 选不好还会震荡

几何意义推导

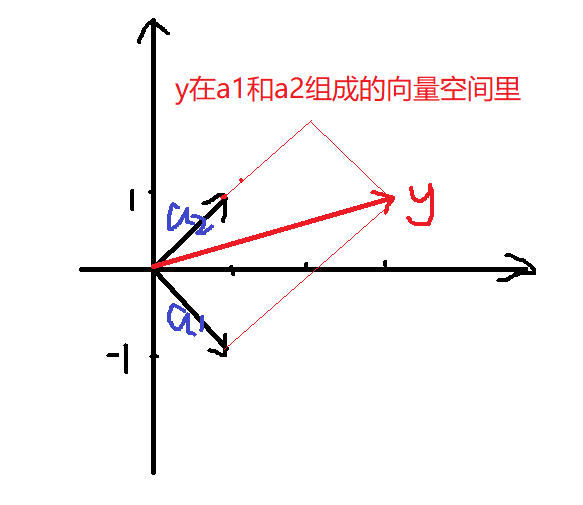
1. 假设普通二维方程，有解的情况

   \[\begin{cases}x_1+x_2=3\\-x_1+x_2=1\end{cases} \]

   写成矩阵形式

   \[\left[\begin{matrix}1&1\\-1&1\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\end{matrix}\right]=\left[\begin{matrix}3\\1\end{matrix}\right] \]

   记列向量\(\left[\begin{matrix}1\\-1\end{matrix}\right]\)为\(a_1\)，列向量\(\left[\begin{matrix}1\\1\end{matrix}\right]\)为\(a_2\)，转化为

   \[a_1x_1+a_2x_2=y \]

   即在向量\(a_1\)和向量\(a_2\)张成的空间里表示出向量\(y\)。

   

2. 推广至方程无解的情况

   假设有三个点(0,2)(1,2)(2,3)，求函数\(y=ax+b\)拟合这三个点。

   写成函数形式

   \[\begin{cases}a\cdot0+b=2\\a\cdot1+b=2\\a\cdot2+b=3\end{cases} \]

   写成矩阵形式

   \[\left[\begin{matrix}0&1\\1&1\\2&1\end{matrix}\right]\left[\begin{matrix}x_1\\x_2\end{matrix}\right]=\left[\begin{matrix}2\\2\\3\end{matrix}\right] \]

   记列向量\(\left[\begin{matrix}0\\1\\2\end{matrix}\right]\)为\(a_1\)，列向量\(\left[\begin{matrix}1\\1\\1\end{matrix}\right]\)为\(a_2\)

   

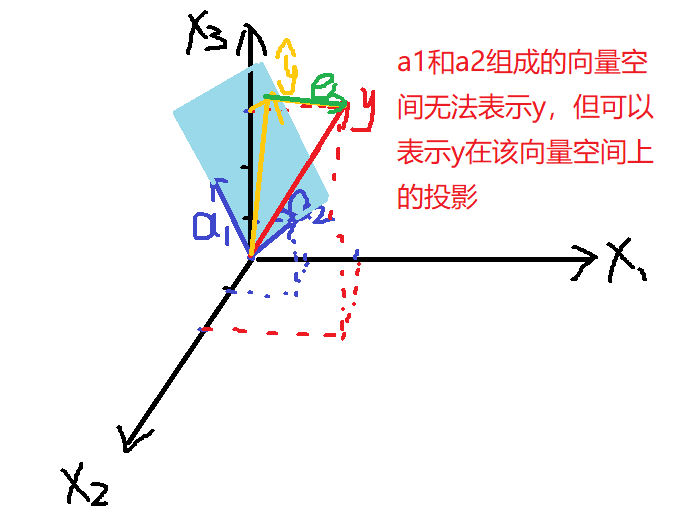
   在向量\(a_1\)和向量\(a_2\)张成的空间里无法表示出向量\(y\)，只能表示出向量\(y\)在该平面上的投影\(\widehat{y}\)，记向量\(y-\widehat{y}=e\)，其中

   \[\widehat{y}=A\theta \]

   则向量\(e\)垂直于向量\(a_1\)和向量\(a_2\)张成的空间。

   \[\begin{cases}a_1\cdot e=0\\a_2\cdot e=0\end{cases} \]

   即 \(A^Te=0\)

   代入得

   \[A^T(y-A\theta)=0\\A^Ty-A^TA\theta=0\\A^Ty=A^TA\theta\\\theta=(A^TA)^{-1}A^Ty \]

极大似然 ( MLE )

极大似然：“最像”、“最大似然”

利用已知观察数据反推模型参数值，调整\(\theta\) 使得样本出现概率最大。

参考：极大似然估计详解

求最大似然函数估计值的一般步骤：

（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数，令导数为0，得到似然方程；
（4）解似然方程，得到的参数即为所求；

Logistic回归(LR，逻辑回归模型，对数几率回归，二分类)

1. (0,1) 的连续函数

2. 构造这样的连续函数，使得函数对于输出大于 0.5 时判为一类，小于 0.5时判为另一类。

   1. Sigmoid Function：\(\phi(z)=\frac{1}{1+e^{-z}}\)
   2. 把 Sigmoid Function 里的变量 z，构造成线性组合

3. Equations：\(P(y=1|x)=\frac{1}{1+exp( - \theta^Tx)}\)

   1. 把线性关系通过 Sigmoid 函数映射到 (0,1)
   2. 线性关系映射为非线性的，还是拟合函数点，但最终结果是做分类

4. 定义几率 odds

   统计和概率论中，定义一个事件的发生比 (Odds) 是该事件发生和不发生的比率。

   \[odds(p)=\frac{p}{1-p} \]

   对 \(odds\) 取对数，也就是 \(log\frac{p}{1-p}=logp-log(1-p)\)

   \(log\frac{P(y=1|x)}{P(y=0|x)}=log\frac{1}{1+exp(-\theta^Tx)}-log(1-\frac{1}{1+exp(-\theta^Tx)})=-\theta^Tx\)

   1. 几率 odds 还是线性的

5. 定义损失函数

   \[J(\theta)=-\frac{1}{N}[\sum_{i=1}^N\sum_{j=0}^1 I(y^{(i)}=j)logP(y^{(i)}=j|x^{(i)},\theta)]\\=-\frac{1}{N}[\sum_{i=1}^N y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))] \]
   • 累加分对了的部分，加了负号，分得越对函数值越小
   • 使用 log，由乘积形式转为加和形式

6. 梯度下降求最优值

   \[\theta \leftarrow \theta - \alpha \frac{\partial J(\theta)}{\partial \theta} \]

Softmax Regression ( Logistic 多分类引申 )

\[P(y=1|x)=\frac{1}{1+exp( - \theta^Tx)}=\frac{exp(\theta^Tx)}{exp( \theta^Tx)+1} \]

\[P(y=0|x)=\frac{1}{exp( \theta^Tx)+1} \]

引申为多分类情况

\[P(y^{(i)}=k|x;\theta)=\frac{exp(\theta_k^T x^{(i)})}{\sum_{j=1}^kexp(\theta_j^T x^{(i)})} \]

岭回归 (Ridge Regression)

前言：回归分析中常用最小二乘法，由 \(A\theta=y\) 采用最小二乘法，定义损失函数为残差的平方，最小化损失函数 \(||A\theta-y||^2\) ，采用梯度下降法求解，也可直接用公式 \(\theta=(A^TA)^{-1}A^Ty\) 求解，若矩阵 \(A\) 不能求逆该如何解决问题。

岭回归

对损失函数加一些正则项 ( regularization )，对系数加一些条件

\[J(\theta)=\frac{1}{2N}||x\theta-Y||_2^2+\frac{1}{2}\alpha ||\theta||_2^2 \]

• 下角标 2 表示 L-2 norm：\(||\theta||_2=\sqrt{\theta_1^2+\theta_2^2+...+\theta_n^2}\)

• 加入正则项 \(\frac{1}{2}\alpha ||\theta||_2^2\) ，新的损失函数 \(J(\theta)\) 既满足 \(x\theta\) 与 \(y\) 尽可能逼近，又限制 \(\theta\) 取得过大的值。

• \(\alpha\) 值像是一个权重，调整逼近程度与 \(\theta\) 值之间的关系

梯度下降

循环求解 ( Iterative Learning ) ，寻找使得 \(J(\theta)\) 最小的 \(\theta\)

\[GD:\quad \theta \leftarrow \theta-\alpha \frac{\partial J(\theta)}{\partial(\theta)} \]

• \(\alpha\) 是求解的步长
• \(GD\) 就是一个求解的方向

1. 二维线性拟合

   \[h(\theta) =\theta_1x+\theta_0 \]
   \[\begin{cases}\theta_0 \leftarrow \theta_0-\alpha \frac{\partial J}{\partial \theta_0}\\\theta_1 \leftarrow \theta_1-\alpha \frac{\partial J}{\partial \theta_1}\end{cases} \]
   • 迭代一定是同时更新 \(\theta_0、\theta_1\)，\(\alpha\) 有自动修正性能，只要不是太大且沿着正确方向迭代，一定能找到最小值。
   \[\frac{J}{\partial \theta_0}=\frac{\partial}{\partial \theta_0}(\frac{1}{2N}\sum_{i=0}^N (h_{\theta}(x^{(i)})-y^{(i)})^2)=\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)}) \]
   \[\frac{J}{\partial \theta_1}=\frac{\partial}{\partial \theta_1}(\frac{1}{2N}\sum_{i=0}^N (h_{\theta}(x^{(i)})-y^{(i)})^2)=\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)} \]
   • \(h(\theta) =\theta_1x+\theta_0\) 写成 \(h(\theta) =\theta_1x_1+\theta_0x_0(x_0=1)\)，\(\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})\) 相当于 \(\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})x_0\)
   • \(\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}\)相当于\(\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})x_1^{(i)}\)

2. 高维线性拟合

   \[h(\theta) =\theta^Tx=\sum_{i=1}^n \theta_j x_j =\theta_1x_1+\theta_2x_2+...+\theta_nx_n+\theta_0 \]
   • \(\theta\) 更像每个特征的权重
   \[\theta_j \leftarrow \theta_j-\alpha \frac{\partial J(\theta)}{\partial \theta_j}=\theta_j-\alpha(\frac{1}{N}\sum_{i=0}^N(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}) \]

求解岭回归的损失函数

梯度下降法

因为加了惩罚项，所以梯度下降迭代公式为

\[\theta_j \leftarrow \theta_j-\alpha(\frac{1}{N}\sum_{i=1}^N(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda}{N} \theta_j) \]

• 梯度下降中用 \(\alpha\) 表示步长，为了区分使用 \(\lambda\) 表示正则项的系数
• 正则项 \(\frac{1}{2}\lambda ||\theta||_2^2\) 对 \(\theta\) 求导正好等于 \(\lambda \theta\)

\[\theta_j\leftarrow (1-\frac{\alpha \lambda}{N})\theta_j-\alpha(\frac{1}{N}\sum_{i=1}^N(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)} \]

• \(\alpha(\frac{1}{N}\sum_{i=1}^N(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}\) 部分每次更新是不变的
• \((1-\frac{\alpha \lambda}{N})\) 中，$ \alpha $ 学习速率一般 0.1~0.5，$ \lambda$ 相对权重一般也比较小，但 \(N\) 一般特别大，所以 \(\frac{\alpha \lambda}{N}\) 是一个很小的小数。每次迭代使得 \(\theta_j\) 缩小。

最小二乘法

最小二乘原始写法：$$\theta=(A^TA)A^TY$$

加上岭回归：$$\widehat{\theta}=(A^TA+\lambda I)^{-1}ATY $$

• \(A^TA\) 是(n+1)*(n+1)的
• \(I\) 也必须是 (n+1)*(n+1)，但对角线并不全是1，而是 \(diag(0,1,1...)\)，不算是标准的单位矩阵。因为 \(\theta_0\) 不需要加惩罚项部分。
• 对于非满秩矩阵加上惩罚项就可以求逆了
• 一般应用最小二乘都是加上岭回归的最小二乘

LASSO回归 ( Least Absolute Shrinkage and Selection Operator)

正则项加的是\(L-1norm\)

\[J(\theta)=\frac{1}{2}||x\theta-Y||_2^2+\lambda ||\theta||_1 \]

• 对特征 \(\theta_j\) 有选择功能，相当于选择出非 0 的特征
  • 希望 \(h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n\) 中特征向量\(\theta^T\)中有尽可能多的 0，即 \(L-0 norm\) 尽可能小
  • 但是\(L-0norm\)不是一个凸函数甚至不是一个连续函数，很难优化
  • 使用 \(L-1norm\) 逼近 \(L-0norm\)
• \(L-1norm\) 可减少复杂度
• 1范数连续且是凸函数，但在一些点不可导，所以不可用梯度下降优化

LASSO优化

参考：[Lasso回归算法： 坐标轴下降法与最小角回归法小结]

\[J(\theta)=Min||x\theta-Y||_2^2+\lambda ||\theta||_1=Min||x\theta-Y||_2^2+\lambda \sum_j|\theta_j| \]

一. Coordinate Descent ( 坐标轴梯度下降 )

先求任何给定 $\theta_j $，在该维度找到最小值，在 \(\theta_j\) 维度将最小值固定；选取另外一个维度 \(\theta_k\)，从 \(\theta_j\) 维度最小值出发，寻找 $\theta_k $ 维度最小值，不断调整。

• 先求 \(\theta\) 与 \(Y\) 之间的距离，选取相似度最大的 \(\theta_i\) 作为起始维度 ( 影响有限 )
• 每个维度都要搜索

二.Forward Selection ( 前向选择 )

求 \(y\) 在特征维度组成的平面的投影 $\widehat{y} $

\[\widehat{y}=\theta_1x_1+\theta_2x_2\\(y-\widehat{y})=e\\e \perp L(x_1,x_2) \]

• 导出最小二乘法计算公式
• 在每一个维度方向求一个 $\theta_i $，使得向量加和等于 $\widehat{y} $
• 只需要执行一次操作，效率高，速度快。但当自变量不是正交的时候，由于每次都是在做投影，所有算法只能给出一个局部近似解

三.Forward Strategy ( 前向梯度 )

• 基于计算的形式，求 \(y\) 在特征维度组成的平面的投影 $\widehat{y} $。
• 在平面内沿着 cost function 减少的方向移动。
• 每一次更新同时计算 \(\varepsilon x_i\) , 计算在哪个维度损失最小，就往哪个维度走 \(\varepsilon\)。
• 当算法在 \(\varepsilon\) 很小的时候，可以很精确的给出最优解，迭代次数也大大的增加。和前向选择算法相比，前向梯度算法更加精确，但是更加复杂。

四.Least Angle Regression ( 角回归，LARS )

• 先一步找到最合适的 \(\theta_1x_1\)
• 找到 \(x_2\) 与 \(\theta_1x_1\) 的角平分线
• 在角分线上不断加 \(\varepsilon\) 使得损失函数最小
• 最小角回归法对前向梯度算法和前向选择算法做了折中，保留了前向梯度算法一定程度的精确性，同时简化了前向梯度算法一步步迭代的过程

线性模型总结

1. 线性模型就是在高维空间里用线性方程拟合数据
2. 维度过高时添加约束项，约束项使用 \(L-2norm\) 可直接优化，使用 \(L-1 norm\) 就需要角回归等特殊优化方法
3. 对于如何选择合适系数 \(\theta^T\) 使得 \(\widehat{y}\) 更逼近期望结果，一般使用损失函数衡量。损失函数一般是 \(L-2norm\)