Die Hard Problem(水壶问题)
Die Hard Problem
引入
有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 z升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 z升 水。
你允许:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1: (From the famous "Die Hard" example)输入: x = 3, y = 5, z = 4
输出: True
示例 2:输入: x = 2, y = 6, z = 5
输出: False来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/water-and-jug-problem
解析
首先考虑将两个水壶的状态用数学的方法来表示出来,我们用一个数对(x , y)来分别代表小的水壶的状态和大的水壶的状态,针对第一个例子x = 3, y = 5我们可以按如下的方式来获得我们希望得到的4升水。
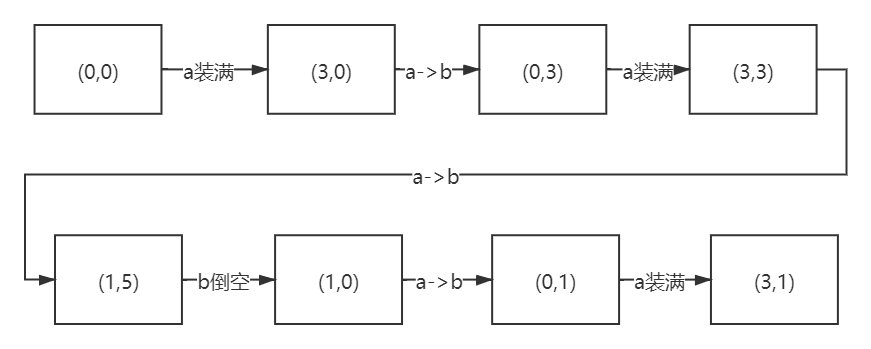
至此,我们就实现了采用两个水壶来装配出4升水的目标。
综合上面的过程来看,我们可以采用一种状态机来模拟两个水壶之间倒水的过程,下面是一些表示方法。
-
我们假设小的水壶的盛水量为a,大的水壶的盛水量为b
-
我们用(x , y)来代表两个水壶在某一时刻的水量
-
两个水壶之间的操作共分为三类
- 将某个水壶倒满
- 将某个水壶的水倒光
- 将一个水壶的水倒入另一个水壶中
状态的变化如图所示:
case a & b:

case c:
c的情况要分两类讨论,一种是如果目标水壶中的剩余容量大于倒入水壶的容量,则可以全部倒入,否则只能刚好倒满但有剩余,两类情况如下图显示
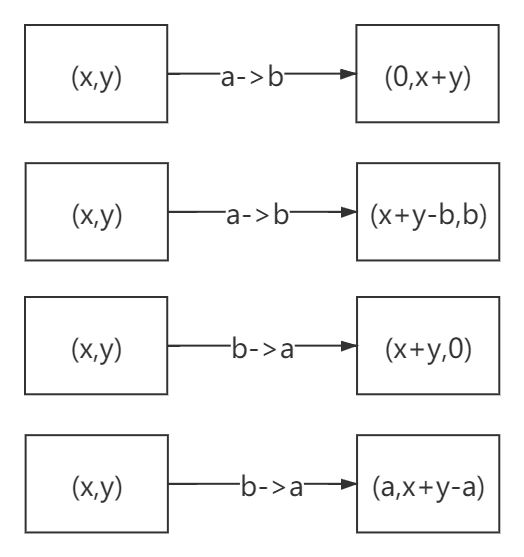
发现
我们发现,从初始值(x , y)经过相互之间的倾倒之后,两个水壶的水量取值情况如下
0, x , y , x + y , a + y , b + x, x + y - a, x + y - b
对于初始状态(0 , 0)来说,经过一次操作过后两个水壶的总水量可以有3种取值
0 , a , b
我们可以通过一个什么桥梁来连接两次转换之间的关系呢?答案是a与b的一个公因子。
我们通过一个简单的证明来说明两者之间的关系,即
若m是a与b的公因子,那么m | x且m | y
我们用归纳法来简单证明一下这个关系:
当n = 0 时,x = 0,y = 0,关系成立
不妨设在状态(x , y) 时关系成立,那么当一次变化之后,对于x , y的所有新的可能的取值,我们也容易得到他们是能够被m整除的
所以我们的关系对于每一步的(x , y)都是成立的
那么这个关系说明了一个什么事情呢?
假设某一时刻的两个水壶的装水量为z
那么我们一定会有式子m | z
又因为这个式子是对于所有的m成立的,所以我们可以得到:
gcd(a , b) | z
也就是说,我们通过这两个水壶之间的操作能够得到的水的总量一定是gcd(a,b)的一个倍数,所以我们在判断的时候对于不是gcd(a,b)的倍数的值就可以直接判定为不可能了
那么反过来,若水量的目标是gcd(a,b)的倍数,我们能否确定能够由这两个水壶得到的?
答案是肯定的
我们不妨这样来表示
z = sa + tb, 其中 s > 0,并且0 < z < b (否则就可以直接装满b或者不装一步到位)
这时,z就是gcd(a,b)的一个倍数
根据贝祖定理,gcd(a,b)可以表示成sa+tb的形式,所以我们的z的表示形式可以包括所有gcd(a,b)的倍数,现在我们来证明凡是这种形式的值都能够由我们的两个水壶经过操作来获得
为了获得这样一个目标值,我们采用如下的算法
我们每次装满a水壶,然后倒入b中,若b中装满,则倒去所有后再继续装入
我们将如上的步骤重复s遍即可获得z的水量
这时,z' = sa - ub,其中u为b倒水的次数
现在我们就来证明
z = z'
即证明
sa + tb = sa - ub
我们对上式做一个变换得到
z' = z - (t + u) b
因为z'代表的是b水壶中装水的数量,所以0 ≤ z' ≤ b
这时候我们容易知道t + u只能为0,否则容易推出矛盾
至此我们已经证明了,凡是能够被a,b两个桶经过操作装出来的水的总量是gcd(a,b)的倍数,同时,凡是gcd(a,b)的倍数的水量也能够由a,b两个桶经过操作获得。
结论
我们只需要判断输入的水量是否为gcd(a,b)的倍数即可,代码如下
def gcd(a,b):
while b != 0:
r = a % b
a = b
b = r
return a
if __name__ == "__main__":
a = int(input())
b = int(input())
c = int(input())
print(c%gcd(a,b)==0)



