方程求根的迭代法
初次发布于我的个人文档。(每次都是个人文档优先发布哦)
本文想简要介绍一下如何用计算机是如何用迭代法计算方程和方程组的根的。
不动点迭代
在高中阶段你可能学习过这样的叫蛛网图的东西:
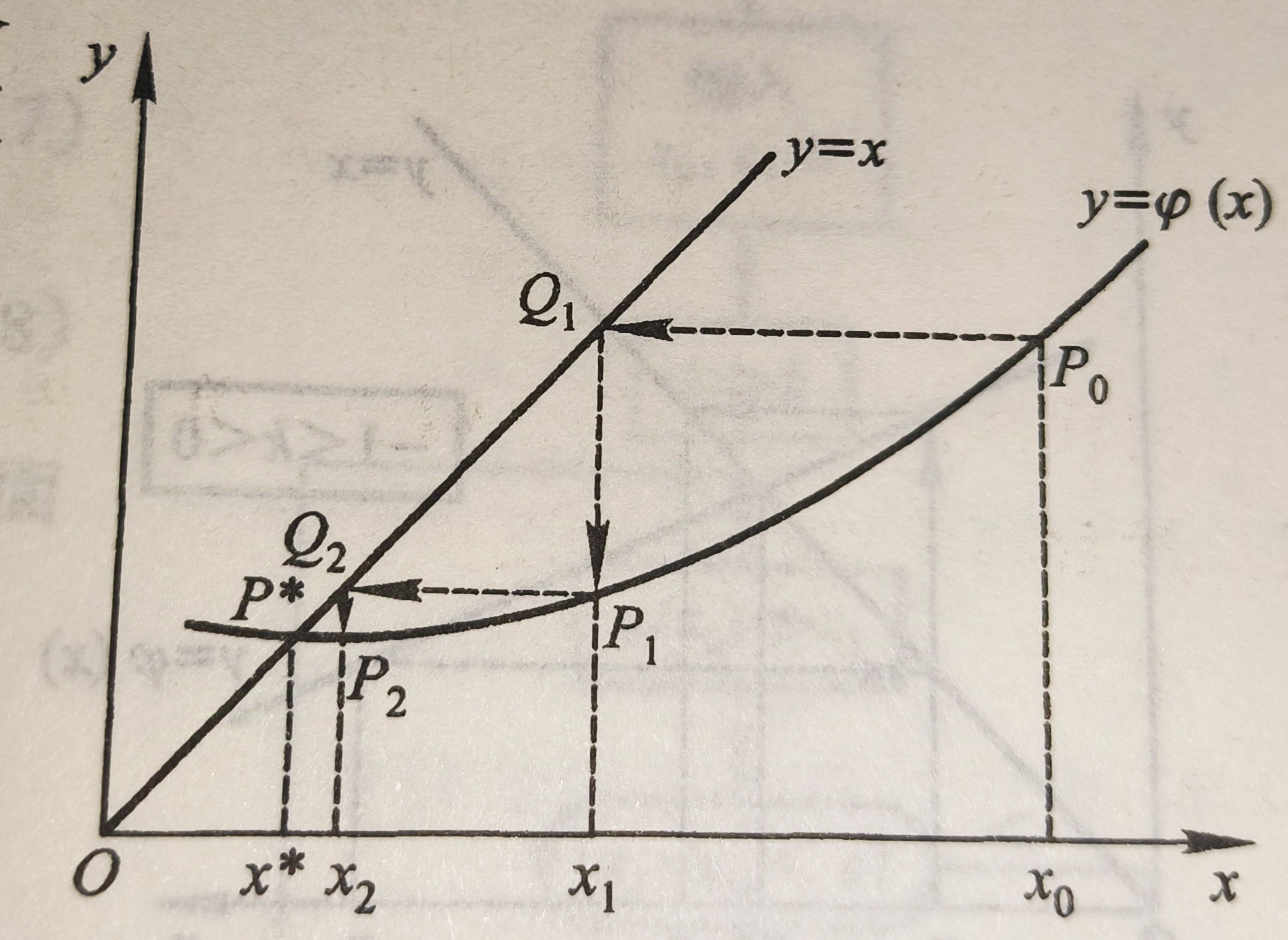
蛛网图迭代的极限就是函数的不动点。
所谓不动点迭代就是利用了这样的性质。
一般地,我们想求解方程f(x)=0,如果我们可以将这个方程转化为x=g(x),那么g(X)的不动点就是f(x)的零点。
而g(x)的不动点又是蛛网图迭代的极限。
如果用代数语言表示的话,就是迭代公式
$$x_{k+1}=g(x_k)$$
这就是不动点迭代求方程的根的方法。
当然,如果要更严谨化的说明的话,就是下面的压缩映像原理:
设g(x)在[a,b]上具有连续的一阶导数,且满足以下条件:
1.$\forall x \in [a,b],g(x) \in [a,b]$
2.$\exist 0 \le L <1,s.t. \forall x\in [a,b],|g'(x)|\le L$
则迭代过程
$x_{k+1}=g(x_k)$收敛,且有误差估计式:
$|x^*-x_k|\le \frac{L^k}{1-L}|x_1-x_0|$
从误差估计式看,k越大估计值$x_k$会离准确值$x^*$越来越近。
这就足以为不动点迭代法背书了。
牛顿迭代法
将不动点迭代进一步推广就能得到牛顿迭代法。
前面我们知道,我们想求解方程f(x)=0,如果我们可以将这个方程转化为x=g(x),然后用迭代公式$x_{k+1}=g(x_k)$求解。
但是我们不知道如何把方程转化为x=g(x),牛顿迭代法就是解决了这个问题。
思路其实也非常简单,我们知道微分有dy=f'(x)dx,于是$f(x)-f(x_k) \approx f'(x_k)(x-x_k)$。
从而$f(x)=f(x_k)+f'(x_k)(x-x_k)=0$
那么$x=x_k-\frac{f(x_k)}{f'(x_k)}$,完成啦!
我们把f(x)=0转化为了x=g(x)的形式了,从而再使用不动点迭代得到f(X)根的迭代公式:
$x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}$
这就是牛顿迭代法。
弦截法
对于某些函数其导数不便于求解,所以我们可以用差商替代导数,这就是弦截法了。
用$f'(x) \approx \frac{f(x_k)-f(x_0)}{x_k-x_0}$代入牛顿迭代法,就是弦截法了。
如果用$f'(x) \approx \frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}$代入牛顿迭代法,就是快速弦截法了。
雅可比迭代法
对于线性方程组,方法其实是类似的。
线性方程组AX=b如果我们可以将其化为X=BX+f,那么用不动点迭代就有迭代公式
$X_{k+1}=BX_k+f$
这是我们线性方程组迭代法的基石。
它的误差:
$e_{k+1}=|x*-x_{k+1}|=|BX+f-(BX_{k}+f)|=B|X^-X_k|=Be_k$
从而,$e_k=B^ke_0$
那么如果$B^k$能收敛于0的话该迭代法就收敛了,可以演算得到这等价于B的谱半径(最大特征值)小于1。
但是还是一样的,不动点迭代法说的轻巧,但是你怎么把AX=b转化成X=BX+f呢?
其中的一种方法就是雅可比迭代法了。
对方程组AX=b,我们将A分解为对角阵D,下三角矩阵L,上三角矩阵U使得
A=D-L-U。
(值得一提的是,这个分解是相当容易的,D就是A的对角元,L取A的下三角去掉主对角线,U取A的上三角去掉主对角线即可)
那么AX=b就是
(D-L-U)X=b
然后移项得
DX=(L+U)X+b
从而$X=D{-1}(L+U)X+Db$
完事了,已经变成X=BX+f的形式了,所以就有迭代公式
$X_{k+1}=D{-1}(L+U)X_k+Db$
这就是雅可比迭代法了。
但是这个方法可以稍微变一下,我们移项的时候不一定要把L和U全部移走,这就是高斯-赛德尔迭代法了。
高斯-赛德尔迭代法
还是安装雅可比迭代的步骤我们得到,(D-L-U)X=b移项但是只移U得到
(D-L)X=UX+b
然后得到$X=(D-L){-1}UX+(D-L)b$
于是就有迭代公式$X_{k+1}=(D-L){-1}UX_k+(D-L)b$
但是我们一般不会这么使用,而是再等式两边再乘以D-L得到
$(D-L)X_{k+1}=UX_k+b$
从而$DX_{k+1}=LX_{k+1}+UX_k+b$
所以$X_{k+1}=D{-1}LX_{k+1}+DUX_k+D^{-1}B$
这才是我们一般最爱用的高斯-赛德尔迭代公式。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· [翻译] 为什么 Tracebit 用 C# 开发
· 腾讯ima接入deepseek-r1,借用别人脑子用用成真了~
· Deepseek官网太卡,教你白嫖阿里云的Deepseek-R1满血版
· DeepSeek崛起:程序员“饭碗”被抢,还是职业进化新起点?
· 深度对比:PostgreSQL 和 SQL Server 在统计信息维护中的关键差异