数据结构 - 11 - B-树（B-Tree）
1多路平衡查找
1.1分级存储
计算机的二级存储系统：内存和外存
内存容量小速度快，外存容量大速度慢。
减少I/O：内存与外存的访问速度相差悬殊，故应该尽可能地减少不同存储级别之间地数据传输。
外存的特性：读取物理地址连续的一千个字节，与读取单个字节花费的时间几乎没有区别。
所以，系统从磁盘读取数据到内存时是以磁盘块（block）为基本单位的，位于同一个磁盘块中的数据会被一次性读取出来，而不是需要什么取什么。外存适合批量访问。
1.2多路搜索树
当数据规模大到内存已经不足以容纳时，常规平衡二叉树的效率将大打折扣。其原因在于，查找过程中对外存的访问次数过多。
上面提到，外存更适合批量访问，那么不妨用时间成本相对极低的多次内存操作替代时间成本相对极高的单次外存操作。相应地，需要将二叉搜索树改造为多路搜索树。
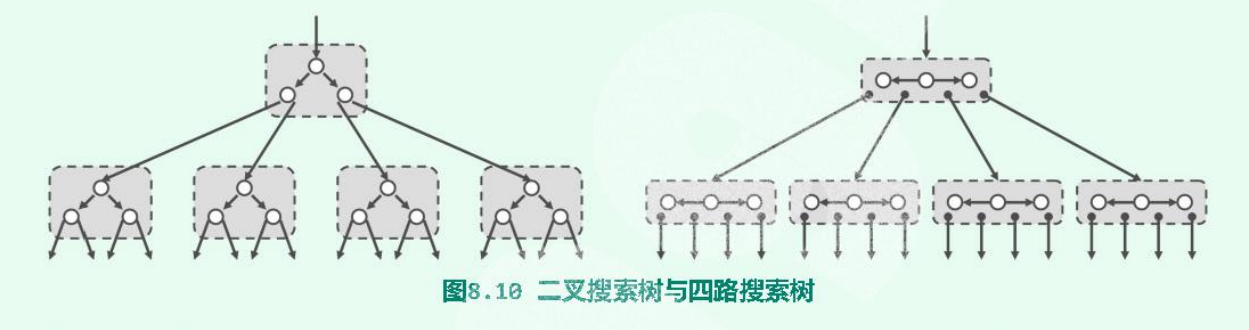
1.3多路平衡搜索树
B-树，即m路平衡搜索树（m>=2）。
一棵m阶的B-Tree有如下特性：
（1）每个节点最多有m个孩子。
（2）除了根节点和叶子节点外，其它每个节点至少有Ceil(m/2)个孩子（Ceil即向上取整）。
（3）若根节点不是叶子节点，则至少有2个孩子。
（4）所有叶子节点都在同一层，且不包含其它关键字信息。
（5）每个非终端节点包含n个关键字信息（P0,P1,…Pn, k1,…kn）
（6）关键字的个数n满足：ceil(m / 2) - 1 <= n <= m - 1
（7）ki(i=1,…n)为关键字，且关键字升序排序。
（8）所有外部节点（叶节点）的深度相等，即在同一层。
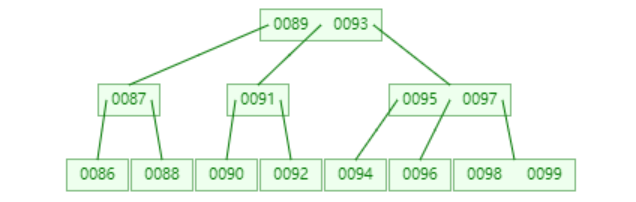
2查找与插入
可以将大数据集组织为B-树并存放于外存，对于活跃的B-树，其根节点会常驻于内存。
任何时候，通常只有一个节点在内存中。
B-树的查找过程与二叉搜索树类似。因为B-树中的关键码也是有序的，所以B-树是天然二分的。不同之处在于每个节点中可能存放了不止一个关键码，此时需要在内存中经过多次比较才能确定转向下一层的哪个节点（即用多次内存访问代替一次外存访问）。
不难看出，只有在切换节点时，才需要访问外存，同一节点内部的查找完全在内存中进行。
性能分析：B-树查找操作的主要时间开销在于将节点装入内存，与此相比，节点内部的查找由于完全在内存内部进行，其开销可以忽略不计。
类似二叉搜索树，B-树每切换一个节点，即深入一层，所以，对于树高为h的B-树，外存访问不超过O(h - 1)次。
树高：存有n个关键码的m阶B-树的高度h = Θ(logmN)，所以每次查找耗时不超过O(logmN)。
（证明略，见《数据结构（C++语言版）第3版》 邓俊辉）
插入：类似二叉搜索树，插入之前先进行一次查找，若查找成功，则表示已经存在该关键码，放弃插入。
若不存在，失败的查找必将终止于某个叶节点，此时在该叶节点中进行一次查找（必定失败）即可获得该关键码应该插入的位置。
B-Tree特性（6）：m阶B-树的每个节点中的关键码最多m - 1个。
插入完成后，若此时该节点中的关键码个数不超过m - 1，则插入完成，否则该节点发生一次上溢。
此时需要分裂节点来调整B-树的结构。
3上溢与分裂
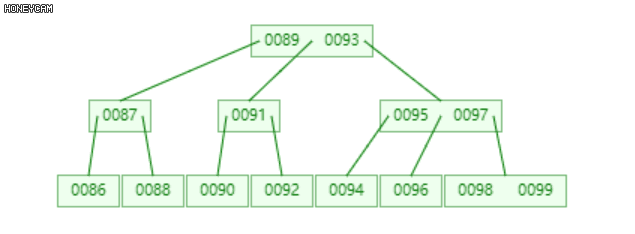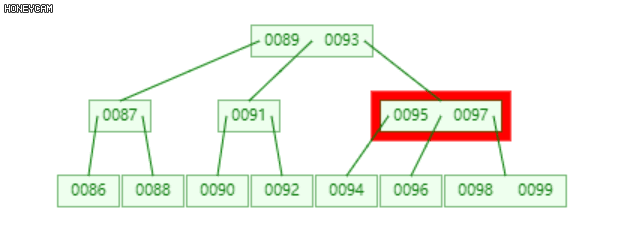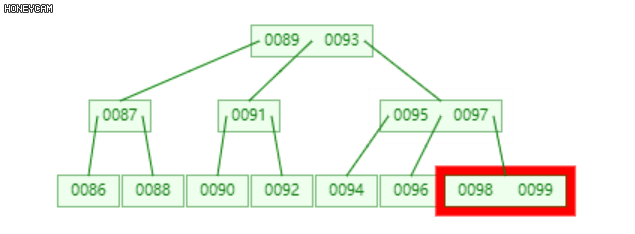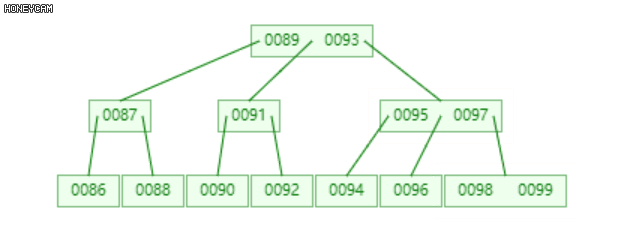
将发生上溢的节点，以关键码的中位数为界（关键码为升序，即中间的数），将节点分裂为三部分（左、中、右），中位数升入上层父节点中，插入合适的位置（保证父节点中的关键码升序），然后分别以左右两部分作为其左右子节点。
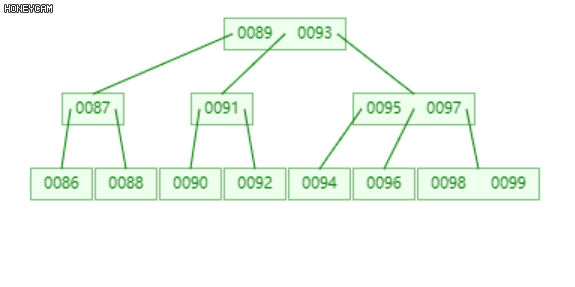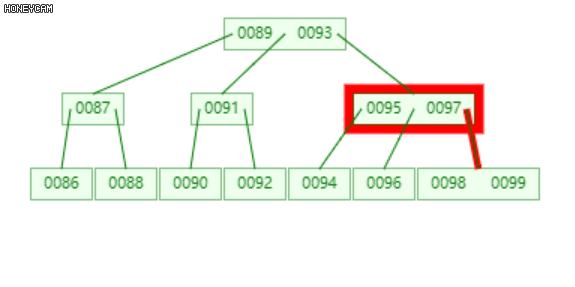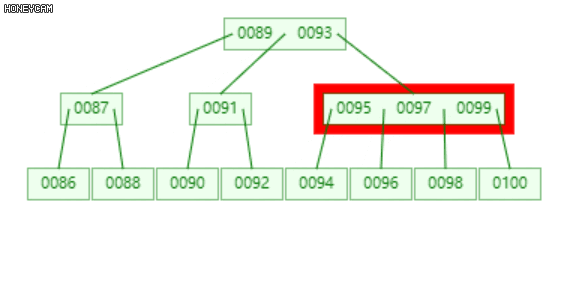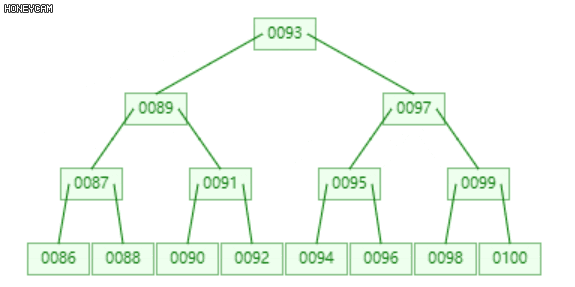
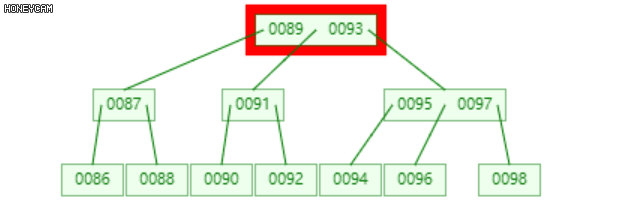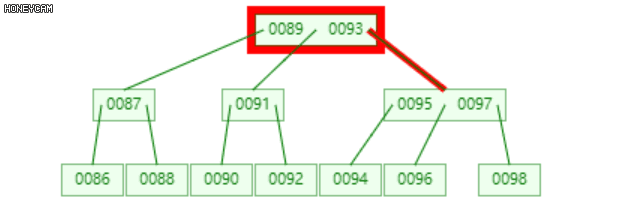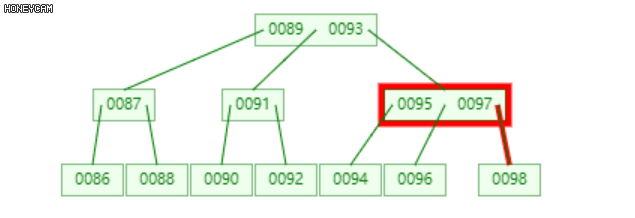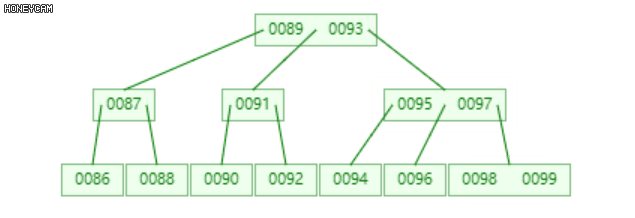
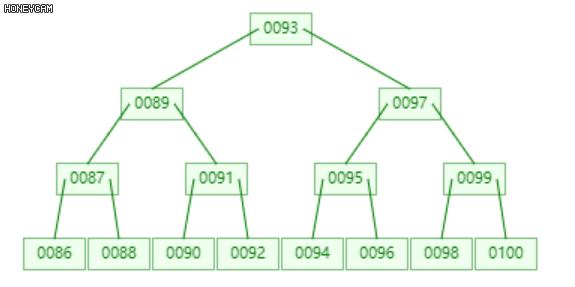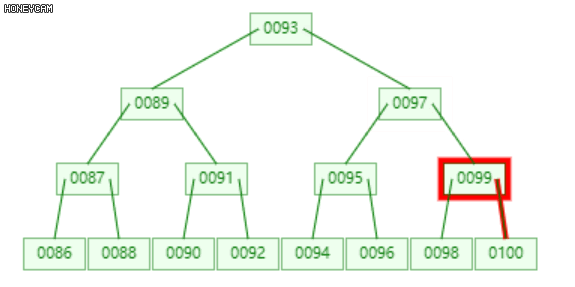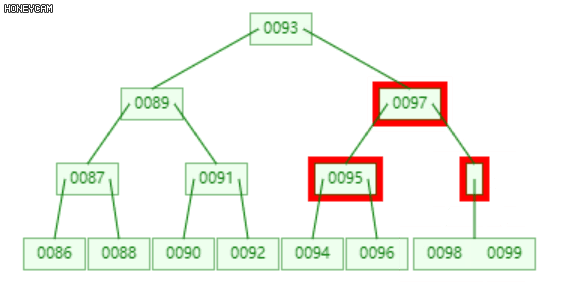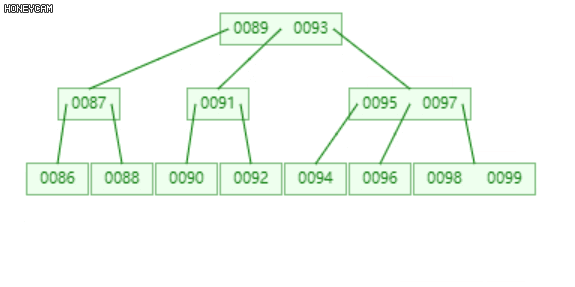
如上图是一棵2阶B-树，插入100后，最右边的叶子节点发生上溢，{98， 99， 100}，将其分裂为三部分，{{98}， {99}， {100}}，其中，99升到上层的父节点{95， 97}中，{98}和{100}作为其左右子节点。
不难发现，99上升入父节点后，父节点也发生了上溢，此时需要继续分裂，递归此过程。至多递归O(logn)层。
4下溢与合并
m阶B-树的每个节点中的关键码的个数上限为n - 1，同时其下限为ceil(m / 2)。
超出上限时发生上溢，那么相应地低于下限时发生下溢。
发生上溢时需要分裂节点，发生下溢时需要合并节点。
